专题21 锐角三角函数 2023年中考数学一轮复习专题训练（湖南省专用）

这是一份专题21 锐角三角函数 2023年中考数学一轮复习专题训练（湖南省专用），共31页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
专题21 锐角三角函数 2023年中考数学一轮复习专题训练（湖南省专用）
一、单选题
1．（2022·湘潭）中国古代数学家赵爽在为《周髀算经》作注解时，用4个全等的直角三角形拼成正方形（如图），并用它证明了勾股定理，这个图被称为“弦图”，若“弦图”中小正方形面积与每个直角三角形面积均为1，α为直角三角形中的一个锐角，则tanα＝（　　）

A．2 B．32 C．12 D．55
2．（2022·娄底）如图，等边△ABC内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称，则圆中的黑色部分的面积与△ABC的面积之比是（　　）

A．3π18 B．318 C．3π9 D．39
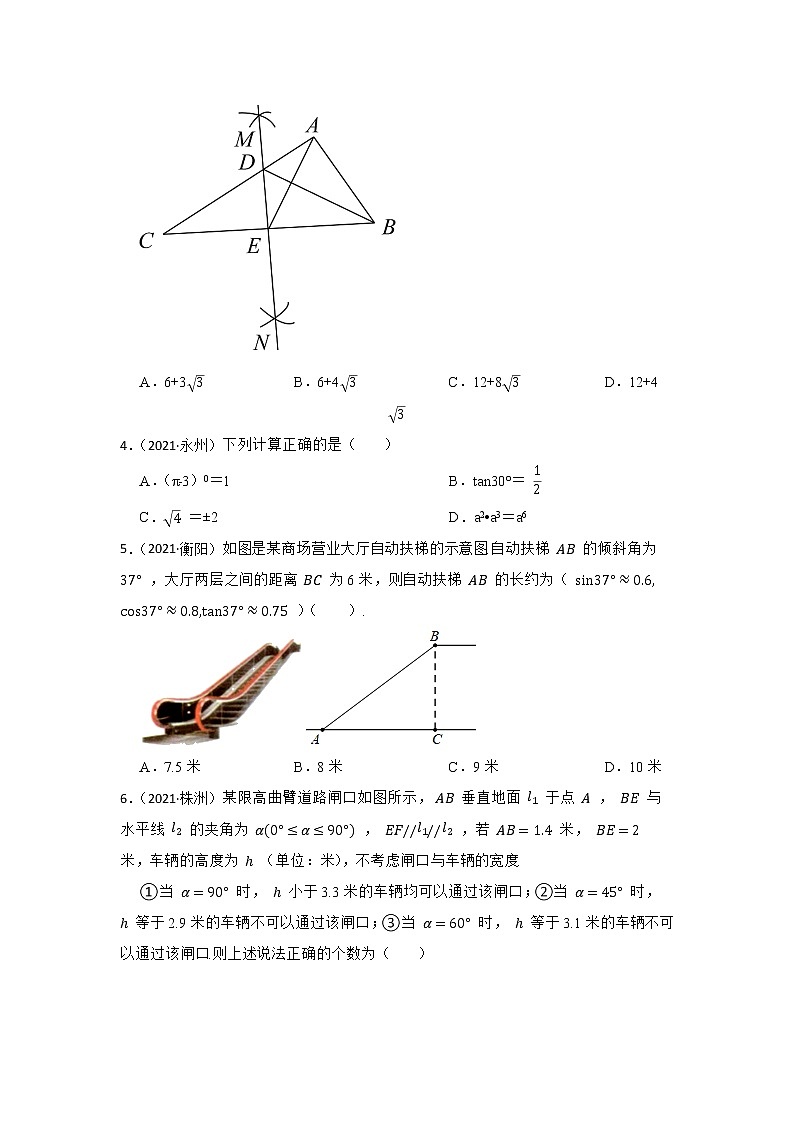
3．（2022·衡阳模拟）如图，在△ABC中，∠BAC＝90°，∠C＝30°，按以下步骤作图：分别以点B，C力圆心，以大于12BC的长为半径作弧，两弧交于M，N两点，作直线MN，与边AC，BC 分别交于D，E两点，连接BD，AE，若AE＝6，则△BCD的周长为（　　）

A．6+33 B．6+43 C．12+83 D．12+43
4．（2021·永州）下列计算正确的是（　　）
A．（π﹣3）0＝1 B．tan30°＝ 12
C．4 ＝±2 D．a2•a3＝a6
5．（2021·衡阳）如图是某商场营业大厅自动扶梯的示意图.自动扶梯 AB 的倾斜角为 37° ，大厅两层之间的距离 BC 为6米，则自动扶梯 AB 的长约为（ sin37°≈0.6,cos37°≈0.8,tan37°≈0.75 ）（　　）.

A．7.5米 B．8米 C．9米 D．10米
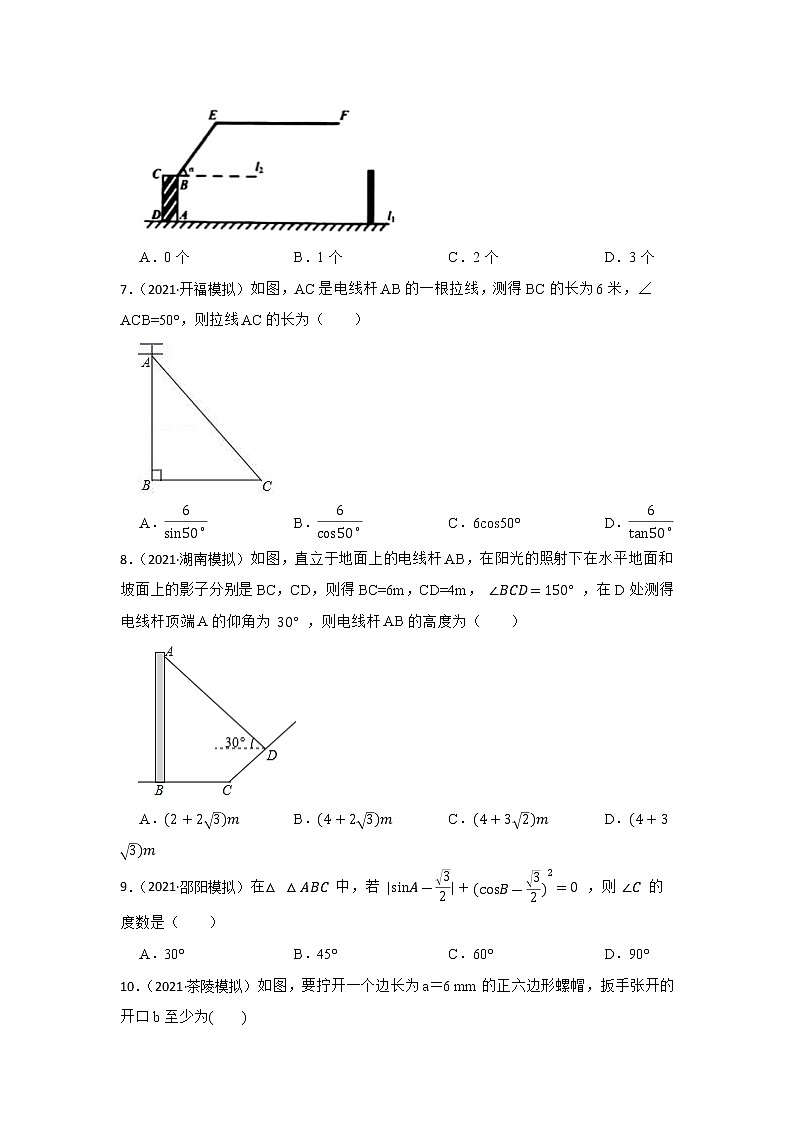
6．（2021·株洲）某限高曲臂道路闸口如图所示， AB 垂直地面 l1 于点 A ， BE 与水平线 l2 的夹角为 α(0°≤α≤90°) ， EF//l1//l2 ，若 AB=1.4 米， BE=2 米，车辆的高度为 h （单位：米），不考虑闸口与车辆的宽度.
①当 α=90° 时， h 小于3.3米的车辆均可以通过该闸口；②当 α=45° 时， h 等于2.9米的车辆不可以通过该闸口；③当 α=60° 时， h 等于3.1米的车辆不可以通过该闸口.则上述说法正确的个数为（　　）

A．0个 B．1个 C．2个 D．3个
7．（2021·开福模拟）如图，AC是电线杆AB的一根拉线，测得BC的长为6米，∠ACB=50°，则拉线AC的长为（　　）

A．6sin50∘ B．6cos50∘ C．6cos50° D．6tan50∘
8．（2021·湖南模拟）如图，直立于地面上的电线杆AB，在阳光的照射下在水平地面和坡面上的影子分别是BC，CD，则得BC=6m，CD=4m， ∠BCD=150° ，在D处测得电线杆顶端A的仰角为 30° ，则电线杆AB的高度为（　　）

A．(2+23)m B．(4+23)m C．(4+32)m D．(4+33)m
9．（2021·邵阳模拟）在△ △ABC 中，若 |sinA-32|+(cosB-32)2=0 ，则 ∠C 的度数是（　　）
A．30° B．45° C．60° D．90°
10．（2021·茶陵模拟）如图，要拧开一个边长为a＝6 mm的正六边形螺帽，扳手张开的开口b至少为(　　)

A．6 2 mm B．12mm C．6 3 mm D．4 3 mm
二、填空题
11．（2022·益阳）如图，在Rt△ABC中，∠C＝90°，若sinA＝45，则cosB＝　 　．

12．（2022·湘西）阅读材料：余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理，运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题．余弦定理是这样描述的：在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍．
用公式可描述为：a2＝b2＋c2﹣2bccosA
b2＝a2＋c2﹣2accosB
c2＝a2＋b2﹣2abcosC
现已知在△ABC中，AB＝3，AC＝4，∠A＝60°，则BC＝　 　．
13．（2022·岳阳）喜迎二十大，“龙舟故里”赛龙舟.丹丹在汩罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛.如图所示，赛道AB为东西方向，赛道起点A位于点P的北偏西30°方向上，终点B位于点P的北偏东60°方向上，AB=200米，则点P到赛道AB的距离约为　 　米（结果保留整数，参考数据：3≈1.732）.

14．（2022·娄底）菱形ABCD的边长为2，∠ABC=45°，点P、Q分别是BC、BD上的动点，CQ+PQ的最小值为　 　.

15．（2022·株洲）中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段，一角圆池占之.”意思是说：“一块正方形田地，在其一角有一个圆形的水池（其中圆与正方形一角的两边均相切）”，如图所示.问题：此图中，正方形一条对角线AB与⊙O相交于点M、N（点N在点M的右上方），若AB的长度为10丈，⊙O的半径为2丈，则BN的长度为　 　丈.

16．（2022·衡阳）回雁峰座落于衡阳雁峰公园，为衡山七十二峰之首.王安石曾赋诗联“万里衡阳雁，寻常到此回”.峰前开辟的雁峰广场中心建有大雁雕塑，为衡阳市城徽.某课外实践小组为测量大雁雕塑的高度，利用测角仪及皮尺测得以下数据：如图， AE=10m ， ∠BDG=30° ， ∠BFG=60° .已知测角仪 DA 的高度为 1.5m ，则大雁雕塑 BC 的高度约为　 　m .（结果精确到 0.1m .参考数据： 3≈1.732 ）

17．（2022·衡阳模拟）如图是大坝的横断面，斜坡AB的坡比i＝1：2，∠ADC＝45°，若坡面CD的长度为62米，则斜坡AB的长度为 　 　米.

18．（2021·南县）如图，Rt△ABC中，∠BAC＝90°，tan∠ABC＝ 32 ，将△ABC绕A点顺时针方向旋转角α（0°＜α＜90°）得到△AB′C′，连接BB′，CC′，则△CAC′与△BAB′的面积之比等于 　 　.

19．（2021·郴州）如图，在△ABC中，AB＝5，AC＝4，sinA＝ 45 ，BD⊥AC交AC于点D.点P为线段BD上的动点，则PC+ 35 PB的最小值为 　 　.

20．（2021·娄底）高速公路上有一种标线叫纵向减速标线，外号叫鱼骨线，作用是为了提醒驾驶员在开车时减速慢行.如图，用平行四边形 ABCD 表示一个“鱼骨”， AB 平行于车辆前行方向， BE⊥AB，∠CBE=α ，过B作 AD 的垂线，垂足为 A' （A点的视觉错觉点），若 sinα=0.05，AB=300mm ，则 AA'=　 　mm .

三、综合题
21．（2021·湘西）如图，AB 为⊙ O 的直径， C 为⊙O上一点， AD 和过点 C 的切线互相垂直，垂足为 D .

（1）求证：AC 平分 ∠DAB ；
（2）若AD=8 ， tan∠CAB=34 ，求：边 AC 及 AB 的长.
22．（2021·娄底）如图①， E、F 是等腰 Rt△ABC 的斜边 BC 上的两动点， ∠EAF=45°， CD⊥BC 且 CD=BE .

（1）求证： △ABE≌△ACD ；
（2）求证： EF2=BE2+CF2 ；
（3）如图②，作 AH⊥BC ，垂足为H，设 ∠EAH=α， ∠FAH=β ，不妨设 AB=2 ，请利用（2）的结论证明：当 α+β=45° 时， tan(α+β)=tanα+tanβ1-tanα⋅tanβ 成立.
23．（2021·岳阳）某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥，如图，该河旁有一座小山，山高 BC=80m ，坡面 AB 的坡度 i=1:0.7 （注：从山顶 B 处测得河岸 E 和对岸 F 的俯角分别为 ∠DBE=45° ， ∠DBF=31° .

（参考数据： sin31°≈0.52 ， cos31°≈0.86 ， tan31°≈0.60 ）
（1）求山脚 A 到河岸 E 的距离；
（2）若在此处建桥，试求河宽 EF 的长度.（结果精确到 0.1m ）
24．（2021·岳阳）如图，在 Rt△ABC 中， ∠ACB=90° ， ∠A=60° ，点 D 为 AB 的中点，连接 CD ，将线段 CD 绕点 D 顺时针旋转 α(60°b，

∴小正方形的边长=a-b，
∴a-b2=1，12ab=1，
∴a-b2=12ab，
∴2a2-5ab+2b2=0，
∴(a-2b)(2a-b)=0，
∴ab=2或ab=12（舍去），
∴tanα＝ab=2.
故答案为：A.

【分析】设直角对角线的两条直角边为a、b，且a>b，根据小正方形面积与每个直角三角形面积均为1，得出a-b2=12ab，然后解方程得出ab=2，再根据正切的定义求解即可.
2．【答案】A
【解析】【解答】解：令内切圆与BC交于点D，内切圆的圆心为O，连接AD，OB，
由题可知，圆中黑色部分的面积是圆面积的一半，

令BC=2a，则BD=a，
在等边三角形ABC中
AD⊥BC，OB平分∠ABC，
∴∠OBD=12∠ABC=30°，
由勾股定理，得AD=3a，
在Rt△BOD中，OD=tan30°×BD=33a，
∴圆中的黑色部分的面积与△ABC的面积之比为π(33a)2×1212×2a×3a=3π18.
故答案为：A.
【分析】令内切圆与BC交于点D，内切圆的圆心为O，连接AD，OB，由题可知：圆中黑色部分的面积是圆面积的一半，令BC=2a，则BD=a，根据等边三角形的性质可得AD⊥BC，∠OBD=30°，利用勾股定理可得AD，根据三角函数的概念可得OD，然后结合圆的面积公式进行计算.
3．【答案】C
【解析】【解答】解：由作图可知MN是BC的垂直平分线，
∴CD=BD，CE=BE，∠DEC=90° ，
在Rt△ABC 中，AE=6 ，
∴CE=BE=AE=6 ，
∴BC=12 ，
在Rt△CDE 中，∠C=30° ，
cosC=CECD=cos30°=32 ，
∴CD=43 ，
∴BD=CD=43 ，
∴△BCD的周长为：CD+BD+BC=43+43+12=12+83 .
故答案为：C.
【分析】由作图可知MN是BC的垂直平分线，则CD=BD，CE=BE，∠DEC=90°，根据直角三角形斜边上中线的性质可得CE=BE=AE=6，则BC=12，根据三角函数的概念可得CD，进而不难求出△BCD的周长.
4．【答案】A
【解析】【解答】解：A.因为π﹣3≠0，所以（π﹣3）0＝1，因此选项A符合题意；
B.tan30°＝ 33 ，因此选项B不符合题意；
C. 4 ＝2，因此选项C 不符合题意；
D.a2•a3＝a2+3＝a5，因此选项D 不符合题意；
故答案为：A.
【分析】根据非零数的0次幂为1可判断A；根据特殊角的三角函数值可判断B；根据算术平方根的概念可拍的C；根据同底数幂的乘法法则可判断D.
5．【答案】D
【解析】【解答】解：根据题意，得： sin37°=BCAB≈0.6
∵BC=6 米
∴AB=BC0.6=60.6=10 米
故答案为：D.
【分析】由sin37°=BCAB≈0.6求出AB即可.
6．【答案】C
【解析】【解答】如图过E点作 EM⊥AB 交 AB 的延长线于点M，

∵EF//l1//l2
∴∠MEB=α
则 h=AM=AB+BE×sinα
①当 α=90° 时， A,B,E 三点共线，
h=AE=AB+BE=1.4+2=3.4>3.3
∴h 小于3.3米的车辆均可以通过该闸口，故①正确.
②当 α=45° 时，
h=AB+BE×sinα=1.4+2×22≈1.4+1.41=2.813.1
∴h 等于3.1米的车辆可以通过该闸口，故③错误.
综上所述：说法正确的为：①②，共2个.
故答案为：C.
【分析】如图过E点作EM⊥AB交AB的延长线于点M，①当α=90° 时，A、B、E三点共线，根据h=AE=AB+BE可求得h的值，比较h与3.3的大小即可判断求解；②当 α=45° 时，根据h=AB+BE×sinα可求得h的值，比较h与2.9的大小即可判断求解；③当 α=60° 时，根据h=AB+BE×sinα可求得h的值，比较h与3.1的大小即可判断求解.

7．【答案】B
【解析】【解答】解：∵∠ABC=90°，∠ACB=60°，BC=6m，
∴cos50°= BCAC = 6AC ，
∴AC= 6cos50∘ .
故答案为：B.
【分析】直接利用锐角三角函数关系得出cos50°= BCAC ，进而得出答案.
8．【答案】B
【解析】【解答】解：如图所示，延长AD交BC的延长线于点E，过点D作DF⊥BE于点F，

∵∠BCD=150° ，
∴∠DCF=30° ，
又∵CD=4 ，
在 Rt△DCF 中，
∴DF=12CD=2 ， CF=CD2-DF2=23 ，
根据题意及图形可得： ∠E=30° ，
∴EF=DFtanE=23 ，
∴BE=BC+CF+EF=6+43 ，
∴AB=BE×tanE=(6+43)×33=23+4 ，
即电线杆的高度为 (23+4) 米.
故答案为：B.
【分析】延长AD交BC的延长线于点E，过点D作DF⊥BE于点F，则∠DCF=30°，由含30°角的直角三角形的性质求出DF，由勾股定理求出CF，根据∠E的正切函数可得EF，进而求出BE，再由AB=BE·tan∠E进行计算.
9．【答案】D
【解析】【解答】解： ∵|sinA-32|+(cosB-32)2=0
∴sinA-32=0 ， cosB-32=0
∴∠A=60°，∠B=30°
∴∠C=180°-30°-60°=90°
故答案为：D.
【分析】根据偶次幂及绝对值的非负性，由两个非负数的和为0，则这两个数都为0，可得sinA及cosB的值，利用特殊角的三角函数值求出∠A、∠B的度数，然后利用三角形内角和定理求出∠C即可.
10．【答案】C
【解析】【解答】设正多边形的中心是O，其一边是AB，

∴∠AOB=∠BOC=60°，
∴OA=OB=AB=OC=BC，
∴四边形ABCO是菱形，
∵AB=6mm，∠AOB=60°，
∴cos∠BAC= AMAB ，
∴AM=6× 32 = 33 (mm)，
∵OA=OC，且∠AOB=∠BOC，
∴AM=MC= 12 AC，
∴AC=2AM= 63 (mm).
故答案为：C.
【分析】设正多边形的中心是O，其一边是AB，利用正六边形的性质可证得∠AOB=∠BOC=60°，OA=OB=AB=OC=BC，可推出四边形ABCD是菱形，利用解直角三角形求出AM的长即可求出AC的长.
11．【答案】45
【解析】【解答】解：∵Rt△ABC中，∠C＝90°，若sinA＝45，
∴∠A+∠B=90°，
∴sinA=cosB=CBAB=45.
故答案为：45.
【分析】利用锐角三角函数的定义，可求出cosB的值.
12．【答案】13
【解析】【解答】解：∵在△ABC中，AB＝3，AC＝4，∠A＝60°，
∴BC2=AC2+AB2-2AC·ABcos∠A=16+9-2×3×4cos60°，
BC2=25-12
解之：BC=13.
故答案为：13.
【分析】由题意可知利用余弦定理：BC2=AC2+AB2-2AC·ABcos∠A；然后代入计算求出结果.
13．【答案】87
【解析】【解答】解：过点P作PC⊥AB，垂足为P，

设PC=x米，
在Rt△APC中，∠APC=30°，
∴AC=PC⋅tan30°=33x（米），
在Rt△CBP中，∠CPB=60°，
∴BC=CP⋅tan60°=3x（米），
∵AB=200米，
∴AC+BC=200，
∴33x+3x=200，
∴x=503≈87，
∴PC=87米，
∴点P到赛道AB的距离约为87米.
故答案为：87.
【分析】过点P作PC⊥AB，垂足为P，设PC=x米，根据三角函数的概念可得AC=33x米，BC=3x米，由AB=AC+BC=200米可求出x，据此解答.
14．【答案】2
【解析】【解答】解：如图，过点C作CE⊥AB于E，交BD于G，根据轴对称确定最短路线问题以及垂线段最短可知CE为FG+CG的最小值，当P与点F重合，Q与G重合时，PQ+QC最小，

∵菱形ABCD的边长为2，∠ABC=45°，
∴Rt△BEC中，EC=22BC=2
∴PQ+QC的最小值为2.
故答案为：2.
【分析】过点C作CE⊥AB于E，交BD于G，根据轴对称确定最短路线问题以及垂线段最短可知CE为FG+CG的最小值，当P与点F重合，Q与G重合时，PQ+QC最小，根据菱形的性质以及三角函数的概念可得EC，据此解答.
15．【答案】（8-22）
【解析】【解答】解：如图，

设⊙O与AD边的切点为点C，连接OC，
则OC=2（丈），OC⊥AD，
由正方形的性质知∠EAD=90°，对角线AB平分∠EAD，
∴∠OAC=12∠EAD=45°，
∴AO=OCsin∠OAC=2sin45°=2×22=22（丈），
∴AN=ON+AO=2+22（丈），
∴BN=AB-AN=10-(2+22)=8-22（丈）.
故答案为：（8-22）.
【分析】设⊙O与AD边的切点为点C，连接OC，则OC=2丈，OC⊥AD，根据正方形的性质可得∠EAD=90°，对角线AB平分∠EAD，则∠OAC=45°，根据三角函数的概念可得AO，由AN=ON+AO可得AN，然后根据BN=AB-AN进行计算.
16．【答案】10.2
【解析】【解答】∵∠BDG=30° 且 ∠BFG=60° ，
∴∠DBF=∠BFG-∠BDG=30° ，
∴∠DBF=∠BDG ，
即 BF=DF=AE=10m .
∴BG=BF⋅sin60°=53m≈8.66m ，
∴BC=BG+GC=BG+DA=8.66+1.5≈10.2m ，
故答案为 10.2m .
【分析】利用已知条件可证得∠DBF=∠BDG，利用等角对等边可证得BF=DF，可求出BF的长；再利用解直角三角形求出BG的长；然后根据BC=BG+CG，可求出BC的长.
17．【答案】65
【解析】【解答】解：过点B作BE⊥AD于E，过点C作CF⊥AD于F，

则四边形BEFC为矩形，
∴BE=CF ，
在Rt△CDF 中，CD=62（米），∠ADC=45°，
∴CF=CD·sin45°=62×22=6（米），
∴BE=6（米），
在Rt△ABE 中，tanA=BEAE=12 ，
∴AE=2BE=12 （米），
∴AB=AE2+BE2=144+36=65 （米），
则斜坡AB的长度为65 米.
故答案为：65.
【分析】过点B作BE⊥AD于E，过点C作CF⊥AD于F，则四边形BEFC为矩形，BE=CF，根据三角函数的概念可得CF、AE，然后利用勾股定理计算即可.
18．【答案】94
【解析】【解答】解：由旋转的性质可知，∠BAC＝∠B′AC′，
∴∠BAB′＝∠CAC′，
∵AB＝AB′，AC＝AC′，
∴ABAC ＝ AB'AC' ，
∴△ACC′∽△ABB′，
∴S△ACC'S△ABB' ＝（ ABAC ）2，
∵∠CAB＝90°，
∴tan∠ABC＝ ABBC ＝ 32 ，
∴∴S△ACC'S△ABB' ＝（ ABAC ）2＝ 94 .
故答案为： 94 .
【分析】由旋转的性质可知：∠BAC＝∠B′AC′，由角的和差关系可得∠BAB′＝∠CAC′，然后证明△ACC′∽△ABB′，由相似三角形的性质以及三角函数的概念求解即可.
19．【答案】165
【解析】【解答】解：过点P作PD⊥AB于点D，过点C作CH⊥AB于点H，

∵BD⊥AC，
∴∠ADB＝90°，
∵sinA＝ BDAB ＝ 45 ，AB＝5，
∴BD＝4，
由勾股定理得AD＝ AB2-BD2=52-42=3 ，
∴sin∠ABD＝ ADAB=DPBO=35 ，
∴DP＝ 35BP ，
∴PC+ 35 PB＝PC+PD，
即点C、P、D三点共线时，PC+ 35 PB最小，
∴PC+ 35 PB的最小值为CH的长，
∵S△ABC＝ 12×AC×BD=12×B×CH ，
∴4×4＝5×CH，
∴CH＝ 165 .
∴PC+ 35 PB的最小值为 165 .
故答案为： 165 .
【分析】过点P作PD⊥AB于点D，过点C作CH⊥AB于点H，则∠ADB＝90°，根据∠A的正弦函数可得BD的值，由勾股定理可得AD，根据∠ABD的正弦函数可得DP＝35BP，则PC+35PB＝PC+PD，推出PC+35PB的最小值为CH的长，由△ABC的面积公式可得CH的值.
20．【答案】15
【解析】【解答】解：如图所示，
∵A'B⊥AD 且四边形 ABCD 为平行四边形，
∴A'B⊥BC ， ∠A'BC=∠ABC+∠A'BA=90° ，
又∵BE⊥AB ，
∴∠ABE=∠ABC+∠α=90° ，
∴∠A'BA=∠α ，
∴sin∠A'BA=sinα=AA'AB=0.05 ，
又∵AB=300mm ，
∴AA'=AB·sin∠A'BA=300×0.05=15 mm.
故答案为：15.
【分析】根据平行四边形的性质，可求出∠A'BA=∠α，由于sin∠A'BA=sinα=AA'AB=0.05，即可求出结论.
21．【答案】（1）证明：连接OC，如图所示：

∵CD是⊙O的切线，
∴∠OCD=90° ，
∵AD⊥CD，
∴∠ADC=∠OCD=90° ，
∴AD//OC ，
∴∠DAC=∠ACO ，
∵OA=OC ，
∴∠ACO=∠OAC=∠DAC ，
∴AC 平分 ∠DAB
（2）解：连接BC，如图所示：

由（1）可得： ∠BAC=∠DAC ，
∵tan∠CAB=34 ，
∴tan∠CAD=tan∠CAB=34 ，
∵AD=8 ，
∴CD=AD⋅tan∠DAC=6 ，
∴AC=AD2+CD2=10 ，
∴cos∠CAB=cos∠CAD=ADAC=45 ，
∵AB 为⊙ O 的直径，
∴∠ACB=90° ，
∴AB=ACcos∠CAB=252
【解析】【分析】（1） 连接OC，根据切线的性质及AD⊥CD，可求出AD//OC ，结合OA=OC，可得∠ACO=∠OAC=∠DAC，即可求出结论；
（2）连接BC，由（1）知∠BAC=∠DAC，即得cos∠CAB=cos∠CADtan∠CAD=tan∠CAB=34，据此求出CD，利用勾股定理求出AC，由AB 为⊙ O 的直径，可得 ∠ACB=90°， 可得ACAB=ADAC=45，从而求出AB.
22．【答案】（1）证明：∵△ABC是等腰直角三角形，
∴AB=AC，∠BAC=90°，
∴∠ABC=∠ACB=45°，
∵CD⊥BC，
∴∠DCB=90°，
∴∠DCA=90°-∠ACB=90°-45°=45°=∠ABE，
在△ABE和△ACD中，
AB=AC∠ABE=∠ACDBE=CD ，
∴△ABE≌△ACD（SAS），
（2）证明：∵△ABE≌△ACD，
∴∠BAE=∠CAD，AE=AD，
∵∠EAF=45°，
∴∠BAE+∠FAC=90°-∠EAF=90°-45°=45°，
∴∠FAD=∠FAC+∠CAD=∠FAC+∠BAE=45°=∠EAF，
在△AEF和△ADF中，
AE=AD∠EAF=∠DAFAF=AF ，
∴△AEF≌△ADF（SAS），
∴EF=DF，
在Rt△CDF中，根据勾股定理，
DF2=CD2+CF2 ，
即 EF2=BE2+CF2 ；
（3）解：将△ABE逆时针绕点A旋转90°到△ACD，连结FD，

∴∠BAE=∠CAD，BE=CD，AE=AD，
∵△ABC为等腰直角三角形，
∠ACB=∠B=∠ACD=45°，∠DCF=∠DCA+∠ACF=45°+45°=90°，
∵AB=2 ，
∴AC= AB=2 ，
在Rt△ABC中由勾股定理 BC=AB2+AC2=(2)2+(2)2=2
∵AH⊥BC，
∴BH=CH=AH= 12BC=1 ，
∴EF=EH+FH=AHtanα+AH tanβ= tanα+ tanβ，BE=BH-EH=1-tanα，CF=CH-HF=1-tanβ，
∵∠EAF=45°，
∴∠BAE+∠CAF=90°-∠EAF=45°，
∴∠DAF=∠DAC+∠CAF=∠BAE+∠CAF=45°=∠EAF，
在△AEF和△ADF中，
AE=AD∠EAF=∠DAFAF=AF ，
∴△AEF≌△ADF（SAS），
∴EF=DF，
在Rt△CDF中， DF2=CD2+CF2 即 EF2=BE2+CF2 ，
∴(tanα+tanβ)2=(1-tanα)2+(1-tanβ)2 ，
整理得 2tanα⋅tanβ=1-2tanα+1-2tanβ ，
即 tanα⋅tanβ=1-tanα-tanβ ，
∴tanα+tanβ=1-tanα⋅tanβ ，
∴tanα+tanβ1-tanα⋅tanβ=1=tan45°=tan(α+β) ，
∴tan(α+β)=tanα+tanβ1-tanα⋅tanβ .
【解析】【分析】（1） 由△ABC是等腰直角三角形，可得AB=AC，∠BAC=90°，∠ABC=∠ACB=45°， 根据垂直的定义可得∠DCB=90°， 从而可求∠DCA=90°-∠ACB=45°，根据SAS可证△ABE≌△ACD；
（2）证明△AEF≌△ADF（SAS），可得EF=DF，在Rt△CDF中，根据勾股定理DF2=CD2+CF2 ，据此即得结论；
（3）将△ABE逆时针绕点A旋转90°到△ACD，连结FD， 利用等腰直角三角形及解直角三角形，可求出EF=EH+FH=AHtanα+AH tanβ= tanα+ tanβ，BE=BH-EH=1-tanα，CF=CH-HF=1-tanβ，证明
△AEF≌△ADF（SAS），可得EF=DF，在Rt△CDF中， DF2=CD2+CF2 即 EF2=BE2+CF2 ，
即得(tanα+tanβ)2=(1-tanα)2+(1-tanβ)2 ，据此进行整理即可求出结论.
23．【答案】（1）解：∵BC=80m ，坡面 AB 的坡度 i=1:0.7 ，
∴CA=80×0.7=56 m，
∵∠DBE=45° ，
∴∠CBE=45° ，
∴∠CBE=∠BEC=45° ，
∴CE=CB=80m ，
∴AE=CE-CA=80-56=24(m) ，
∴山脚 A 到河岸 E 的距离为24m
（2）解：∵∠DBF=31° ， BD//CF ，
∴∠BFC=31° ，
∴CF=CBtan31°≈800.6≈133.3(m) ，
∴EF=CF-CE≈133.3-80=53.3(m) ，
∴河宽 EF 的长度约为53.3m
【解析】【分析】（1）根据AB的坡度求出CA，由∠CBE=∠BEC=45°，可得CE=CB=80m，利用AE=CE-CA计算即得结论；
（2）根据平行线的性质得出∠BFC=∠DBF=31°，从而求出CF=CBtan31°≈133.3(m)，利用EF=CF-CE计算即得结论.
24．【答案】（1）ED=BD；33
（2）解：①正方形，理由如下：
∵α=90° ， DM 平分 ∠CDE ，
∴∠CDE=90° ， ∠CDF=∠EDF ，
∵CD=ED ， DF=DF ，
∴△CDF≌△EDF(SAS) ，
∴∠DCF=∠DEF ，
∵CF//DE ，
∴∠FCD+∠CDE=180° ，
∴∠FCD=90° ，
∴∠DCF=∠DEF=∠CDE=90° ，
∴四边形 CDEF 为矩形，
又∵CD=ED ，
∴四边形 CDEF 为正方形；
②显然，在正方形 CDEF 中， △CFH∽△GDH ，
∴DHFH=DGCF ，
又∵CD=CF ，
∴DHFH=DGCD=33 ，
由（1）得： ∠A=60°,CD=AD, 则 △ACD 为等边三角形，
∴∠ADC=60° ，
∵∠CDE=90° ，
∴∠GDB=30° ，
∴∠GDB=∠GBD ， GD=GB ，
又∵DE=DB ，
∴∠DBE=∠DEB=12(180°-∠GDB)=75° ，
∴∠GBE=75°-30°=45° ，
∵∠GDH=45° ，
∴∠GBE=∠GDH
在 △GBE 与 △GDH 中，
∠GDH=∠GBEGD=GB∠DGH=∠BGE
∴△GBE≌△GDH(ASA) ，
∴BE=DH ，
∴BEFH=DHFH=DGCD=33
（3）解：同（2）中①理， △CDF≌△EDF ，
∴∠CDF=∠EDF ， ∠CFD=∠EFD ，
∵CF//DE ，
∴∠CFD=∠EDF ，
∴∠CFD=∠CDF ， ∠EDF=∠EFD ，
∴CF=CD ， ED=EF ，
∴四边形 CDEF 为菱形，
∵△ACD 为等边三角形，
∴AC=CD=AD=BD=2 ，菱形的边长也为2，
由题意， ∠HDG=α2 ， ∠DEB=∠DBE=12∠ADE=30°+α2 ，
∵∠DBG=30° ，
∴∠EBG=α2 ，
即： ∠HDG=∠EBG ，
∴△EBG∽△HDG ，
∵在菱形 CDEF 中， △HFC∽△HDG ，
∴△EBG∽△HFC ，
∴BEFH=BGFC ，
如图，作 DK⊥CG ，

∵∠DCK=30° ，
∴∠CDK=60° ， ∠KDG=α-60° ，
∵CD=2 ，
∴DK=1 ， CK=3 ，
在 Rt△KDG 中， GKDK=tan∠KDG=tan(α-60°)=m ，
∴GK=m ，
∴CG=3+m ，
在 Rt△ABC 中， BC=3AC=23 ，
∴BG=BC-CG=23-3-m=3-m ，
∵CF=CD=2 ，
∴BEFH=BGFC=3-m2
【解析】【解答】（1）∵点 D 为 Rt△ABC 中斜边 AB 的中点，
∴CD=AD=BD ，
∵线段 CD 绕点 D 顺时针旋转得到线段 ED ，
∴CD=ED ，
∴ED=BD ，
∵Rt△ABC 中， ∠ACB=90° ， ∠A=60° ，
∴∠B=30° ，
∵CD=BD ，
∴∠B=∠DCG=30° ，
∴在 Rt△DCG 中， GDCD=tan∠DCG=tan30°=33 ，
故答案为： ED=BD ； 33 ；
【分析】（1）根据直角三角形的性质及旋转的性质可得CD=AD=BD=ED，利用等边对等角可得∠B=∠DCG=30°，在 Rt△DCG 中，由于GDCD=tan∠DCG即可求出结论；
（2）①证明△CDF≌△EDF(SAS) ，可得∠DCF=∠DEF，利用平行线的性质可得∠DCF=∠DEF=∠CDE=90° ，可证四边形 CDEF 为矩形，由CD=ED，可证四边形 CDEF 为正方形；
②证明△CFH∽△GDH，可得DHFH=DGCD=33，再证△GBE≌△GDH(ASA) ，可得
BE=DH，可得BEFH=DHFH=DGCD=33；
（3）证明四边形 CDEF 为菱形，由△ACD 为等边三角形，可得AC=CD=AD=BD=2，证明
△EBG∽△HFC，可得BEFH=BGFC， 如图作 DK⊥CG ，求出∠CDK=60°， ∠KDG=α-60° ，继而求出DK=1 ，CK=3，在 Rt△KDG 中， GKDK=tan∠KDG=tan(α-60°)=m，可得 GK=m ， CG=3+m ，
在 Rt△ABC 中， BC=3AC=23 ，可得 BG=BC-CG=23-3-m=3-m ，利用BEFH=BGFC即得结论.
25．【答案】（1）证明： ∵PB'⊥AC ， ∠BAC=90° ，
∴PB'//AB ，
∴∠CPB'=∠ABP ，
由折叠的性质得： ∠AB'P=∠ABP,PB'=PB ，
∴∠CPB'=∠AB'P ，
∴AB'//BC ，
∴ 四边形 ABPB' 是平行四边形，
又 ∵PB'=PB ，
∴ 平行四边形 ABPB' 是菱形，
∴PB'=AB'
（2）解：如图，设 AC 与 PB' 的交点为点 O ，过点 O 作 OD⊥AB' 于点 D ，

∵AB=AC ，
∴Rt△ABC 是等腰三角形， ∠ABC=∠ACB=45° ，
设 AB=AC=4a(a>0) ，则 BC=42a ，
∵BP=3PC ，
∴BP=32a,PC=2a ，
由折叠的性质得： ∠AB'P=∠ABP=45°,PB'=PB=32a,AB'=AB=4a ，
在 △COP 和 △B'OA 中， ∠OCP=∠OB'A=45°∠COP=∠B'OA ，
∴△COP∼△B'OA ，
∴OCOB'=OPOA=PCAB'=2a4a=24 ，
设 OC=2b(b>0) ，则 OB'=4b,OP=32a-4b,OA=4a-2b ，
∴OPOA=32a-4b4a-2b=24 ，
解得 b=427a ，
∴OA=4a-2×427a=207a ，
在 Rt△B'OD 中， B'D=OB'⋅cos∠AB'P=22b=167a ，
∴AD=AB'-B'D=127a ，
则 cos∠B'AC=ADOA=127a207a=35
（3）解： ∵∠ACB=30°,∠BAC=90° ，
∴∠ABC=60° ，
设 AB=CB'=2m(m>0) ，则 BC=4m,AC=BC2-AB2=23m ，
由折叠的性质得： ∠AB'P=∠ABP=60°,AB'=AB=2m ，
∴AB'=CB'=2m ，
由题意，分以下两种情况：
①如图，当点 B' 在直线 AC 的左侧时，过点 B' 作 B'E⊥AC 于点 E ，

∴CE=12AC=3m （等腰三角形的三线合一），
∴B'E=B'C2-CE2=m=12B'C ，
∴ 在 Rt△B'CE 中， ∠B'CE=30° ，
∴∠B'CP=∠B'CE+∠ACB=30°+30°=60° ，
又 ∵AB'=CB' ，
∴∠B'AC=∠B'CE=30° ，
∴∠AB'C=180°-∠B'AC-∠B'CE=120° ，
∴∠CB'P=∠AB'C-∠AB'P=120°-60°=60° ，
∴△CB'P 是等边三角形，
∴PC=CB'=2m ，
∴PCBC=2m4m=12 ；
②如图，当点 B' 在直线 AC 的右侧时，过点 B' 作 B'F⊥AC 于点 F ，

同理可得： ∠B'CF=30° ，
∴∠B'CF=∠ACB ，
∴ 点 B' 在 BC 上，
由折叠的性质得： AP⊥BB' ，
在 Rt△ABP 中， BP=AB⋅cos∠ABC=m ，
∴PC=BC-BP=3m ，
∴PCBC=3m4m=34 ，
综上，存在点 P ，使得 AB=CB' ，此时 PCBC 的值为 12 或 34
【解析】【分析】（1） 证明四边形 ABPB' 是平行四边形，由折叠的性质得出PB'=PB，从而可证平行四边形 ABPB' 是菱形，可得PB'=AB'；
（2）设AC与 PB' 的交点为点 O ，过点 O 作 OD⊥AB' 于点 D ，求得△ABC是等腰直角三角形，设 AB=AC=4a(a>0) ，则 BC=42a，从而可得BP=32a,PC=2a，由折叠的性质得： ∠AB'P=∠ABP=45°,PB'=PB=32a,AB'=AB=4a，证明 △COP~△B'OA ，可得OCOB'=OPOA=PCAB'=2a4a=24，设OC=2b(b>0)，可得 OB'=4b,OP=32a-4b, OA=4a-2b ，代入比例式可得b=427a，从而求出OA，利用解直角三角形求出B'D，从而求出
AD=AB'-B'D 的长，由cos∠B'AC=ADOA即得结论；
（3） 分两种情况：①如图，当点 B' 在直线 AC 的左侧时， 过点 B' 作 B'E⊥AC 于点 E ，②如图，当点 B' 在直线 AC 的右侧时，过点 B' 作 B'F⊥AC 于点 F ，据此分别求解即可