初中数学2 平行线的判定图片免费ppt课件

这是一份初中数学2 平行线的判定图片免费ppt课件，共26页。PPT课件主要包含了◆趣味导入，同位角，内错角，同旁内角互补，“因为”“所以”等内容，欢迎下载使用。

1.通过画图得到判定直线平行的基本事实,并能由这个基本事实推导出平行线的另外两个判定.2.会根据平行线的判定进行简单的推理,体会用“∵”“∴”符号的方便.
◉重点:平行线判定的应用.◉难点:三种判定方法的灵活选用.
“∵”“∴”的历史18世纪初还没有人以“∵”表示“因为”.到了1805年,英国出版的《大众数学手册》中才首次以“∵”表示“因为”,但还没有以“∴”表示“所以”的应用那样广.到了1827年,由剑桥大学出版的欧几里德《几何原本》中分别以“∵”表示“因为”,“∴”表示“所以”.这种用法日渐流行,且沿用至今.
如图,木匠师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线a、b.你知道其中的道理吗?今天学习了平行线的判定,同学们就清楚了.
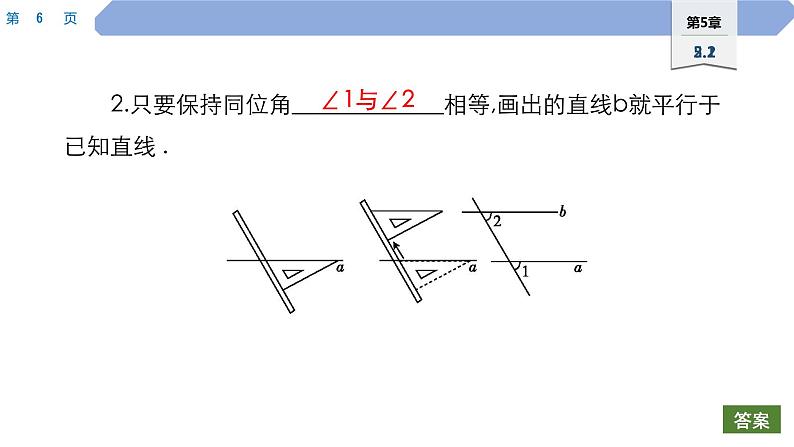
阅读课本“同位角相等,两直线平行”前面的内容,通过画图探求这两条线平行的一个基本事实.如图所示的方法是上节课画一条直线b与已知直线a平行的方法.1.在三角尺紧靠直尺的边和直线所成的角在平移前的位置和平移后的位置构成的一对同位角为　　,其大小始终没变.
▶知识点一　两直线平行的基本事实
2.只要保持同位角　　相等,画出的直线b就平行于已知直线 .
基本事实:两条直线被第三条直线所截,如果　 　相等,那么这两条直线　 　.简单地说,就是同位角　 　,两直线平行.
如图1(知识点二中),直线a、b被直线c所截,如果∠1=45°,∠4=45°,那么a　　b.(填“∥”或“⊥”)
阅读课本“同位角相等,两直线平行”后面的内容,学会用两直线平行的基本事实推导后两种判定的方法,并能简单应用.图1　　
▶知识点二　用内错角相等、同旁内角互补判定两直线平行
1.如图1,直线a、b被直线c所截.(1)如果∠2=∠4,那么a∥b对吗?为什么?(2)如果∠3+∠4=180°,那么a∥b对吗?为什么?
对.因为∠2=∠4,∠2=∠1,所以∠1=∠4,所以a∥b.
对.因为∠3+∠4=180°,∠3+∠1=180°,所以∠1=∠4,所以a∥b.
2.由课本“例3”得到“垂直于同一条直线的两条直线　”,这个结论和上节课得到的“平行于同一条直线的两条直线　　”一样,都可以作为判断两条直线平行的方法.
1.两条直线被第三条直线所截,如果　　相等,那么这两条直线　　.简单地说,就是内错角　　,两直线平行.2.两条直线被第三条直线所截,如果　　,那么这两条直线　　.简单地说,就是同旁内角　,两直线平行.
如图,一直线截直线AB、CD,得到八个角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8.请你根据要求填空.(1)∵∠3 =∠5(已知),∴　 　∥　 　.(内错角相等,两直线平行)(2)∵∠4+∠5=180°(已知),∴　 　∥　　.(同旁内角互补,两直线平行)
互动探究一平行线判定的直接应用
1.如图,直线a、b被直线c所截,下列条件中,不能判定a∥b的是 ()A.∠2=∠4　　　　　B.∠1+∠4=180°C.∠5=∠4D.∠1=∠3
如图,E是AD延长线上一点,∠B=30°,∠C=120°.如果添加一个条件,使BC∥AD,那么可添加的条件为　 　.(只填一个即可)
∠1=30°或∠2=120°
2.如图,CE⊥DG于点C,∠BAF=50°,∠ACE=140°,CD与AB平行吗?为什么?
解:AB∥CD.理由如下:∵CE⊥DG,∴∠ECG=90°.∵∠ACE=140°,∴∠ACG=50°.∵∠BAF=50°,∴∠BAF=∠ACG,∴AB∥CD.
◆互动探究二　　 　用平行线的判定进行说理
如图,AE与CD交于点O,∠A=40°,OC=OE,∠C=20°,求证:AB∥CD.
证明:∵OC=OE,∴∠E=∠C=20°,∴∠DOE=∠C+∠E=40°.∵∠A=40°,∴∠A=∠DOE,∴AB∥CD.
3.如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C,求证:DE∥BC.
证明:∵∠1+∠DHE=180°,∠1+∠2=180°,∴∠DHE=∠2,∴DH∥AC.∴∠3=∠AED,∵∠3=∠C,∴∠C=∠AED,∴DE∥BC.
符号“∵”“∴”分别表示　 　,括号内所写的,就是括号前这一结论成立的依据.“对顶角相等”“等量代换”“等式的性质”常常作为推理的依据.
4.在铺设铁轨时,两条直轨必须是互相平行的.如图,已知∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直线是否平行?为什么?
◆互动探究三　　利用平行线的判定解决实际问题
解:(1)通过度量∠3的度数,若满足∠2+∠3=180°,根据“同旁内角互补,两直线平行”就可以验证这个结论;(2)通过度量∠4的度数,若满足∠2=∠4,根据“同位角相等,两直线平行”就可以验证这个结论;(3)通过度量∠5的度数,若满足∠2=∠5,根据“内错角相等,两直线平行”就可以验证这个结论.
如图,∠ABC=∠DEF,∠E+∠AME=180°,AB、EF相交于点M,试判断BC、EF是否平行,并说明理由.
解:∵∠DEF+∠AME=180°,∠ABC=∠DEF(已知),∴∠ABC+∠AME=180°(等量代换).∵∠BME+∠AME=180°(平角定义),∴∠ABC=∠BME(同角的补角相等),∴BC∥EF(内错角相等,两直线平行).