第18 图形的相似 2023年中考数学一轮复习专题训练（浙江专用）

这是一份第18 图形的相似 2023年中考数学一轮复习专题训练（浙江专用），共51页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
第18 图形的相似 2023年中考数学一轮复习专题训练（浙江专用）
一、单选题
1．（2022·衢州）如图，在△ABC中，AB=AC，∠B=36°．分别以点A，C为圆心，大于12AC的长为半径画弧，两弧相交于点D，E，作直线DE分别交AC，BC于点F，G．以G为圆心，GC长为半径画弧，交BC于点H，连结AG，AH．则下列说法错误的是（　　）

A．AG=CG B．∠B=2∠HAB
C．△CAH≅△BAG D．BG2=CG⋅CB
2．（2022·衢州）西周数学家商高总结了用“矩”（如图1）测量物高的方法：把矩的两边放置成如图2的位置，从矩的一端A（人眼）望点E，使视线通过点C，记人站立的位置为点B，量出BG长，即可算得物高EG．令BG=x（m）， EG=y（m），若a=30cm，b=60cm，AB=1.6m，则y关于x的函数表达式为（　　）

A．y=12x B．y=12x+1.6 C．y=2x+1.6 D．y=1800x+1.6
3．（2022·桐乡模拟）如图，在平面直角坐标系 xOy 中，线段 AB 两端点的坐标分别为 A(3，0) ， B(2，2) ，以点 P(1，0) 为位似中心，将线段 AB 放大得线段 CD ，若点 C 坐标为 (7，0) ，则点 D 的坐标为（　　）

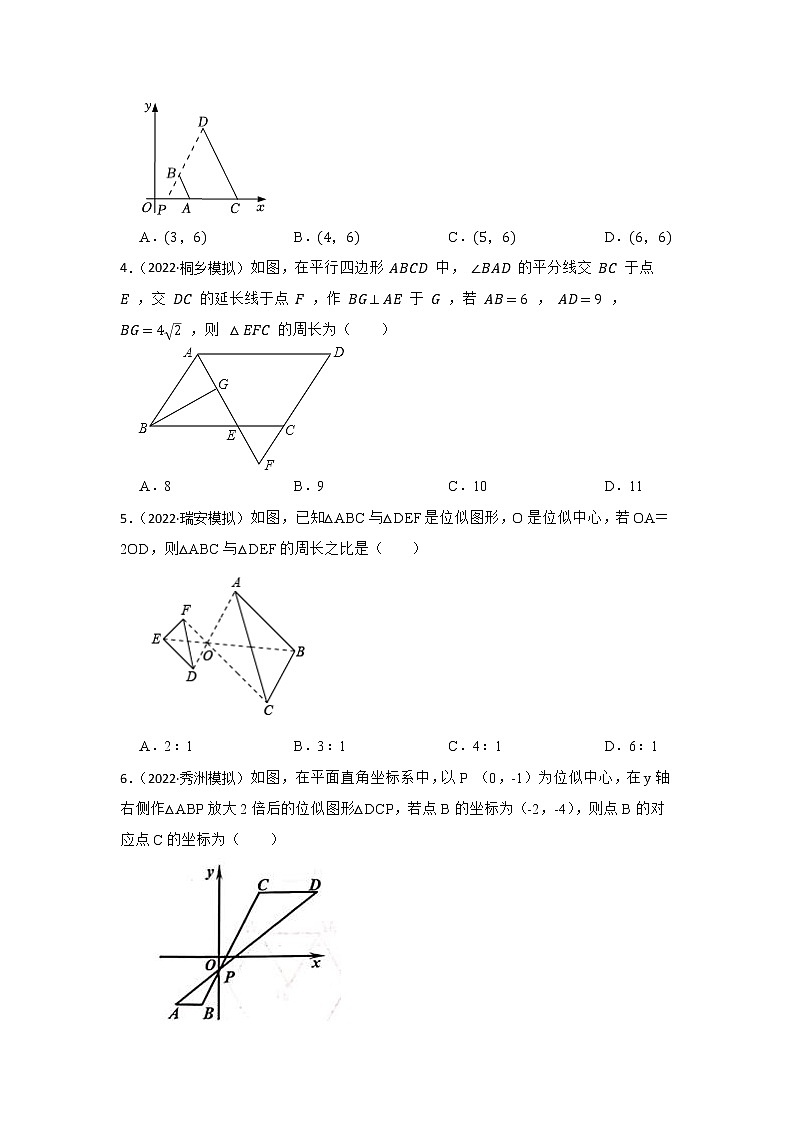
A．(3，6) B．(4，6) C．(5，6) D．(6，6)
4．（2022·桐乡模拟）如图，在平行四边形 ABCD 中， ∠BAD 的平分线交 BC 于点 E ，交 DC 的延长线于点 F ，作 BG⊥AE 于 G ，若 AB=6 ， AD=9 ， BG=42 ，则 △EFC 的周长为（　　）

A．8 B．9 C．10 D．11
5．（2022·瑞安模拟）如图，已知△ABC与△DEF是位似图形，O是位似中心，若OA＝2OD，则△ABC与△DEF的周长之比是（　　）

A．2：1 B．3：1 C．4：1 D．6：1
6．（2022·秀洲模拟）如图，在平面直角坐标系中，以P （0，-1）为位似中心，在y轴右侧作△ABP放大2倍后的位似图形△DCP，若点B的坐标为（-2，-4），则点B的对应点C的坐标为（　　）

A．（4，5） B．（4，6） C．（2，4） D．（2，6）
7．（2022·温州模拟）由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.作EM∥NG∥AD.若GF=2FM，则MN：FD的值为（　　）

A．233 B．52 C．54 D．1
8．（2022·南浔模拟）如图，在平面直角坐标系中，点A的坐标为 (1，0) ，点D的坐标为 (3，0) ，若 △ABC 与 △DEF 是位似图形，则 ACDF 的值是（　　）

A．12 B．13 C．23 D．14
9．（2022·兰溪模拟）古希腊数学家发现“黄金三角形”很美.顶角为36°的等腰三角形，称为“黄金三角形”.如图所示， △ABC 中， AB=AC ， ∠A=36° ，其中 BCAC=5-12≈0.618 ，又称为黄金比率，是著名的数学常数.作 ∠ABC 的平分线，交 AC 于 C1 ，得到黄金三角形 △BCC1 ；作 C1B1∥BC 交 AB 于 B1 ， B1C2∥BC1 交 AC 于 C2 ，得到黄金三角形 △B1C1C2 ；作 C2B2∥BC 交 AB 于 B2 ， B2C3∥BC1 交 AC 于 C3 ，得到黄金三角形 △B2C2C3 ；依此类推，我们可以得到无穷无尽的黄金三角形.若 BC 的长为1，那么 C5C6 的长为（　　）

A．5-2 B．9-45 C．25-4 D．135-29
10．（2022·新昌模拟）如图是沙漏示意图（数据如图），上下两部分为全等三角形，将上半部分填满沙子后，在沙子下落至如图位置时，AB的长为多少？（正在下落的沙子忽略不计）（　　）

A．1cm B．2cm C．3cm D．4cm
二、填空题
11．（2022·湖州）如图，已知在△ABC中，D，E分别是AB，AC上的点，DE∥BC， ADAB=13 ，若DE=2，则BC的长是　 　．

12．（2022·杭州）如图是以点O为圆心，AB为直径的圆形纸片．点C在⊙O上，将该圆形纸片沿直线CO对折，点B落在⊙O上的点D处（不与点A重合），连接CB，CD，AD．设CD与直径AB交于点E．若AD=ED，则∠B=　 　度； BCAD 的值等于　 　．

13．（2022·宁波模拟）如图，在矩形 ABCD中，点E在边AD上，BE⊥AC 于点F，若AD=2，AB=CF，则sin∠ABE 的值为　 　．

14．（2022·江干模拟）如图，在 △ABC 中， AB=AC ， AD 平分 ∠BAC ，点 E 在 AB 上，连结 CE 交 AD 于点 F ，且 AE=AF ，以下命题： ①4∠BCE=∠BAC ； ②AE⋅DF=CF⋅EF ； ③AEAB=EFCF ； ④AD=12(AE+AC). 正确的序号为　 　.

15．（2022·龙湾模拟）如图，岸边堤坝和湖中分别伫立着甲、乙两座电线塔，甲塔底 CD 和堤坝 EF 段均与水平面 MN 平行， B 为 CD 中点， CD=6EF=12 米， DE=5 米．某时刻甲塔顶 A 影子恰好落在斜坡底端 E 处，此时小章测得2米直立杆子的影长为1米．随后小章乘船行驶至湖面点 P 处，发现点 D ， F ， P 三点共线，并在 P 处测得甲塔底 D 和乙塔顶 T 的仰角均为 α=26.7° ，则塔高 AB 的长为　 　米；若小章继续向右行驶10米至点 Q ，且在 Q 处测得甲、乙两塔顶 A ， T 的仰角均为 β=36.8° ．若点 M ， P ， Q ， N 在同一水平线上， TN⊥MN ，则甲、乙两塔顶 A ， T 的距离为　 　米．（参考数据： tan26.7°≈0.5 ， sin26.7°≈0.45 ， tan36.8°≈0.75 ， cos36.8°≈0.8 ）

16．（2022·宁波模拟）如图， 在矩形 ABCD 中 (AD>AB) ， 点 E 为 BC 的中点， 点 F 为边 BC 上的动点， 连结 AF，DE . 将 △ABF 沿着 AF 翻折， 使点 B 的对应点 B' 恰好落在线段 DE 上. 若 A，B'，C 三点共线， 则 cos∠B'FC 的值为　 　；若 AD=4 ， 且这样的点 B' 有且只有一个时， 则 DE 的长为　 　.

17．（2022·余杭模拟）如图，在△ABC中，D为BC上的一点，E为AD上的一点，BE的延长线交AC于点F，已知 BDDC=1a ， AEDE=1b （a，b为不小于2的整数），则 S△ABFS△DFC 的值是　 　

18．（2022·西湖模拟）如图，在矩形ABCD中， AB=2 ， AD=8 ，点E，F在BC上，点G是射线DC与射线AF的交点，若 BE=1 ， ∠EAF=45° ，则AG的长为　 　．

19．（2022·鄞州模拟）如图，正方形 ABCD 的边长为4，正方形 CEFG 的边长为 22 ，将正方形 CEFG 绕点 C 旋转， BG 和 DE 相交于点 K ，则 AK 的最大值是　 　，连结 BE ，当点 C 正好是 △BKE 的内心时， CK 的长是　 　.

20．（2022·淳安模拟）如图是一张矩形纸片ABCD，AB＝3，AD＝4，在BC上任意取一点E，将△DEC沿DE折叠，（1）若点C恰好落在对角线BD上的点C'处，则CE＝　 　；（2）若点C恰好落在对角线AC上的点C'处，则CE＝　 　.

三、综合题
21．（2022·衢州）如图，在菱形ABCD中，AB=5，BD为对角线.点E是边AB延长线上的任意一点，连结DE交BC于点F，BG平分∠CBE交DE于点G．

（1）求证：∠DBG=90°.
（2）若BD=6，DG=2GE．
①求菱形ABCD的面积.
②求tan∠BDE的值.
（3）若BE=AB，当∠DAB的大小发生变化时（0°