



2020-2021学年19.3 矩形 菱形 正方形达标测试
展开2021-2022学年八年级数学下册尖子生同步培优题典【沪科版】
专题19.12菱形的性质与判定大题专练
姓名:__________________ 班级:______________ 得分:_________________
一.解答题(共24小题)
1.(2021春•临沧期末)如图,菱形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,且BE=AC,连接EC.
(1)求证:四边形BECO是矩形;
(2)连接ED交AC于点F,连接BF,若AC=6,AB=5,求BF的长.
【分析】(1)由菱形的性质得∠BOC=90°,OC=AC,推出BE=OC,则四边形BECO是平行四边形,再由∠BOC=90°,即可得出结论;
(2)由勾股定理求出OB=4,则BD=2OB=8,再证△ODF≌△CEF(ASA),得DF=EF,然后由直角三角形斜边上的中线性质即可求解.
【解答】(1)证明:∵四边形ABCD是菱形,
∴∠BOC=90°,OC=OA=AC,
∵BE=AC,
∴BE=OC,
∵BE∥AC,
∴四边形BECO是平行四边形,
∵∠BOC=90°,
∴平行四边形BECO是矩形;
(2)解:∵四边形ABCD是菱形,
∴BC=AB=5,OC=AC=3,OB=OD,AC⊥BD,
在Rt△OBC中,由勾股定理得:OB===4,
∴BD=2OB=8,
由(1)得:四边形BECO是矩形,
∴BE=OC=3,∠OBE=∠ECO=90°,OB=CE,OB∥CE,
∴DE===,∠ODF=∠CEF,OD=CE,
∵∠DOF=∠ECF=90°,
∴△ODF≌△CEF(ASA),
∴DF=EF,
∵∠DBE=90°,
∴BF=DE=.
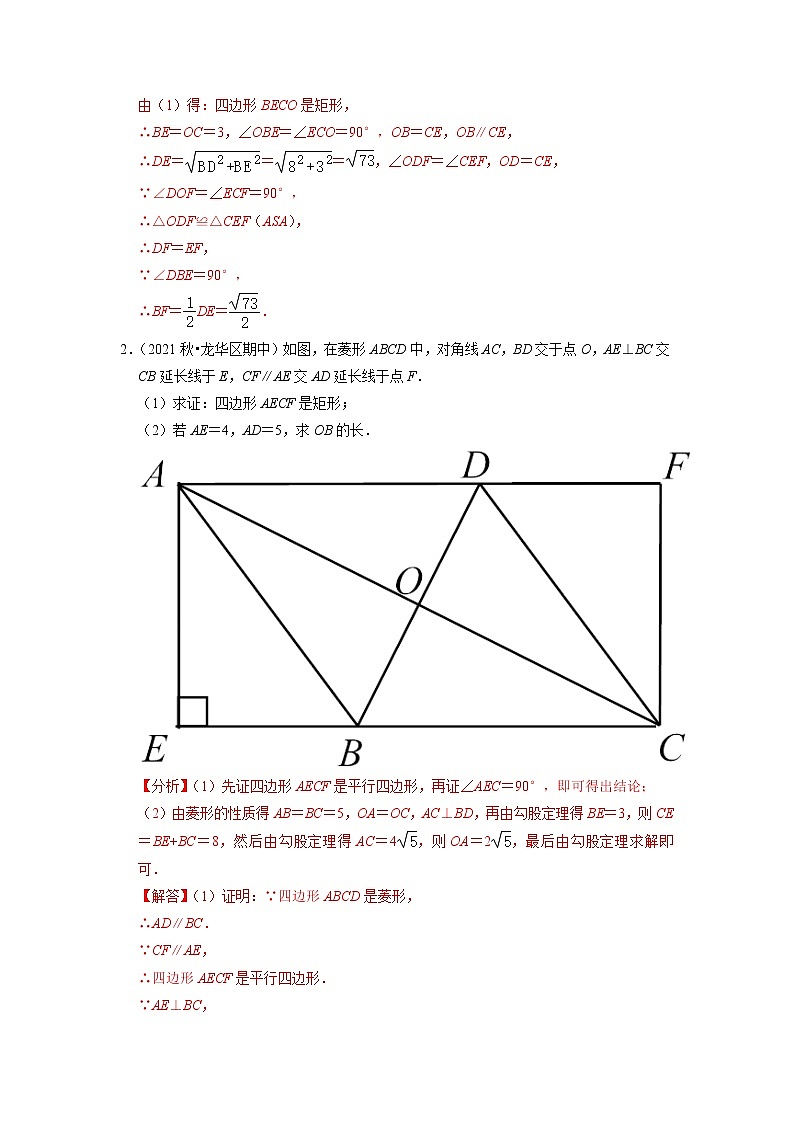
2.(2021秋•龙华区期中)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)若AE=4,AD=5,求OB的长.
【分析】(1)先证四边形AECF是平行四边形,再证∠AEC=90°,即可得出结论;
(2)由菱形的性质得AB=BC=5,OA=OC,AC⊥BD,再由勾股定理得BE=3,则CE=BE+BC=8,然后由勾股定理得AC=4,则OA=2,最后由勾股定理求解即可.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC.
∵CF∥AE,
∴四边形AECF是平行四边形.
∵AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=BC=5,OA=OC,AC⊥BD,
∵AE⊥BC,
∴∠AEB=90°,
∴BE===3,
∴CE=BE+BC=3+5=8,
∴AC===4,
∴OA=AC=2,
在Rt△AOB中,由勾股定理得:OB===.
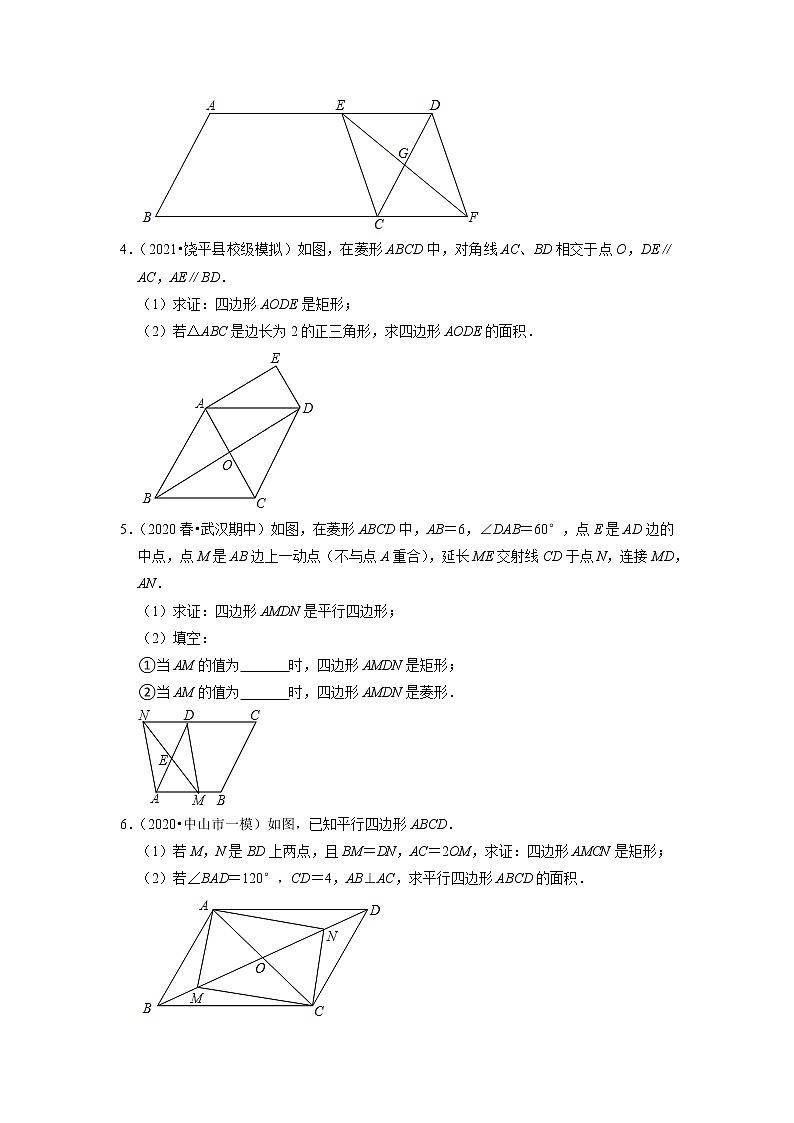
3.(2021春•永城市期末)如图,在▱ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形.
(2)若BC=2AB=8,∠B=60°.填空:
①当AE= 6 时,四边形CEDF是矩形;②当AE= 4 时,四边形CEDF是菱形.
【分析】(1)证△DEG≌△CFG(AAS),得EG=FG,再由DG=CG,即可得出四边形CEDF是平行四边形;
(2)①过A作AM⊥BC于M,证△MBA≌△EDC(SAS),得∠CED=∠AMB=90°,即可得出结论;
②证△CDE是等边三角形,得CE=DE,即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEG=∠CFG,
∵G是CD的中点,
∴DG=CG,
在△DEG和△CFG中,
,
∴△DEG≌△CFG(AAS),
∴EG=FG,
∵DG=CG,
∴四边形CEDF是平行四边形;
(2)解:①当AE=6时,四边形CEDF是矩形,理由如下:
过A作AM⊥BC于M,如图所示:
∵BC=2AB=8,
∴AB=4,
∵∠B=60°,
∴∠BAM=90°﹣60°=30°,
∴BM=2,
∵四边形ABCD是平行四边形,
∴∠CDE=∠B=60°,CD=AB=4,BC=AD=8,
∵AE=6,
∴DE=2=BM,
在△MBA和△EDC中,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:6;
②当AE=4时,四边形CEDF是菱形,理由如下:
∵AD=8,AE=4,
∴DE=4,
∵CD=4,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.
4.(2021•饶平县校级模拟)如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若△ABC是边长为2的正三角形,求四边形AODE的面积.
【分析】(1)根据题意可判断出四边形AODE是平行四边形,再由菱形的性质可得出AC⊥BD,即∠AOD=90°,继而可判断出四边形AODE是矩形;
(2)由菱形的性质和勾股定理求出OB,得出OD,由矩形的面积公式即可得出答案.
【解答】(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)解:∵△ABC是边长为2的正三角形,
∴AB=AC=2,
∠ABC=60°,
∵四边形ABCD为菱形,
∴AO=AC=1,OD=OB,
∵∠AOB=90°,
∴OB===,
∴OD=OB=,
∵四边形AODE是矩形,
∴四边形AODE的面积=×1=.
5.(2020春•武汉期中)如图,在菱形ABCD中,AB=6,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:
①当AM的值为 3 时,四边形AMDN是矩形;
②当AM的值为 6 时,四边形AMDN是菱形.
【分析】(1)由菱形的性质可得∠DNE=∠AME,再由点E是AD边的中点,可得AE=DE,从而可证明△NDE≌△MAE(AAS),则NE=ME,根据对角线互相平分的四边形是平行四边形可得答案;
(2)①当AM的值为3时,四边形AMDN是矩形.根据对角线相等的平行四边形是矩形即可判定;②当AM的值为6时,四边形AMDN是菱形.根据对角线互相垂直的平行四边形是菱形即可判定.
【解答】解:(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠DNE=∠AME,∠NDE=∠MAE,
∵点E是AD边的中点,
∴AE=DE,
∴在△NDE和△MAE中,△NDE≌△MAE(AAS),
∴NE=ME,
∴四边形AMDN是平行四边形;
(2)①当AM的值为3时,四边形AMDN是矩形.理由如下:
∵四边形ABCD为菱形,
∴AB=AD=6,
∵点E是AD边的中点,
∴AE=AD=3,
∴AM=AE=3,
∵∠DAB=60°,
∴△AEM是等边三角形,
∴EM=AE,
∵NE=EM=MN,
∴MN=AD,
∵四边形AMDN是平行四边形,
∴四边形AMDN是矩形.
故答案为:3;
②当AM的值为6时,四边形AMDN是菱形.理由如下:
∵AB=AD=6,AM=6,
∴AD=AM,
∵∠DAB=60°,
∴△AMD是等边三角形,
∴ME⊥AD,
∵四边形AMDN是平行四边形,
∴四边形AMDN是菱形.
故答案为:6.
6.(2020•中山市一模)如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
【分析】(1)由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形;
(2)根据平行四边形的性质得到AD∥BC,AB=CD=4,求得∠ABC=60°,解直角三角形即可得到结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC=AB=4,
∴平行四边形ABCD的面积=AC•AB=44=16.
7.(2020春•濮阳期末)如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,①则当∠ADE= 80 °时,四边形BECD是矩形;
②则当∠ADE= 90 °时,四边形BECD是菱形.
【分析】(1)由AAS证明△BOE≌△COD,得出OE=OD,即可得出结论;
(2)①根据三角形的内角和定理和等腰三角形的性质得到BD⊥AE,根据矩形的判定定理即可得到结论;
②根据三角形的内角和定理得到∠AED=40°,根据平行线的性质得到CBE=∠A=50°,求得∠BOE=90°,根据菱形的判定定理即可得到结论.
【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:①当∠ADE=80°时,四边形BECD是矩形;
理由:∵∠A=50°,∠ADE=80°,
∴∠AED=50°,
∴∠A=∠AED,
∴AD=DE,
∵AB=CD=BE,
∴BD⊥AE,
∴∠DBE=90°,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;
②当∠ADE=90°时,四边形BECD是菱形,
∵∠A=50°,∠ADE=90°,
∴∠AED=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠A=50°,
∴∠BOE=90°,
∴BC⊥DE,
∴四边形BECD是菱形,
故答案为:80,90.
8.(2020秋•福田区月考)如图,点O是菱形ABCD对角线的交点,分别过点B、点C作CO,BO的平行线交于点E,连接AE交BD于点H,交BC于点F.
(1)求证:四边形OCEB是矩形;
(2)若BF=1,求菱形ABCD的周长.
【分析】(1)先证四边形OCEB是平行四边形,再由菱形的性质得∠BOC=90°,即可得出结论;
(2)由菱形的性质得AB=BC=CD=AD,OA=OC,再由矩形的性质得BE=OC=OA,则,然后证△BEF∽△CAF,则,求出BC=3,即可求解.
【解答】(1)证明:∵BE//OC,CE//OB,
∴四边形OCEB是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴平行四边形OCEB是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,OA=OC,
由(1)得,四边形OCEB是矩形,
∴BE=OC=OA,
∴,
∵BE∥AC,
∴△BEF∽△CAF,
∴,
∵BF=1,
∴CF=2,
∴BC=3,
∴菱形ABCD的周长=4BC=4×3=12.
9.(2021•黄冈模拟)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AB=13,OE=,求AE的长.
【分析】(1)先证四边形AEFD是平行四边形,再证出∠AEF=90°,然后由矩形的判定定理即可得到结论;
(2)由菱形的性质得BC=AB=13,AC⊥BD,OA=OC,OB=OD,再由直角三角形斜边上的中线性质得OE=OA=2,AC=2OE=4,然后由勾股定理求出OB=3,则BD=2OB=6,最后由菱形ABCD的面积=BD×AC=BC×AE,即可求解.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AB=13,
∴BC=AB=13,AC⊥BD,OA=OC=AC,OB=OD=BD,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=OA=2,AC=2OE=4,
∴OB===3,
∴BD=2OB=6,
∵菱形ABCD的面积=BD×AC=BC×AE,
即×6×4=13×AE,
解得:AE=12.
10.(2020秋•西城区校级月考)如图,菱形ABCD中,AC与BD交于点O,DE∥AC,DE=AC.
(1)求证:四边形OCED是矩形;
(2)连接AE,交OD于点F,连接CF,若CF=CE=1,求AC长.
【分析】(1)根据菱形的性质得到AC⊥BD,OA=OC,根据矩形的判定定理即可得到结论;
(2)根据直角三角形的性质得到CF=AF=EF,得出AE=2,根据勾股定理即可得到答案.
【解答】(1)证明:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC,
∴∠DOC=90°,
∵DE∥AC,DE=AC,
∴OC=DE,
∴四边形OCED为平行四边形,
又∵∠DOC=90°,
∴四边形OCED是矩形;
(2)解:由(1)得:四边形OCED是矩形,
∴OD∥CE,∠OCE=90°,
∵O是AC中点,
∴F为AE中点,
∴CF=AF=EF,
∵CF=CE=1,
∴EF=1,
∴AE=2,
∴AC===.
11.(2021•兴宁区校级一模)如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若△ABC是边长为4的正三角形,求四边形AODE的面积.
【分析】(1)根据题意可判断出四边形AODE是平行四边形,再由菱形的性质可得出AC⊥BD,即∠AOD=90°,继而可判断出四边形AODE是矩形;
(2)由菱形的性质和勾股定理求出OB,得出OD,由矩形的性质即可得出答案.
【解答】(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=∠AOD=90°,
∴四边形AODE是矩形;
(2)解:∵△ABC是边长为4的正三角形,
∴AB=AC=4,
∠ABC=60°,
∵四边形ABCD为菱形,
∴AO=AC=2,OD=OB,
∵∠AOB=90°,
∴OB==2,
∴OD=OB=2,
∵四边形AODE是矩形,
∴四边形AODE的面积=22=4.
12.(2021•房山区一模)如图,四边形ABCD是平行四边形,过点A作AE⊥BC交CB的延长线于点E,点F在BC上,且CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接BD,若∠ABD=90°,AE=4,CF=2,求BD的长.
【分析】(1)由平行四边形的性质得到AD∥BC且AD=BC,证出BC=EF,推出四边形AEFD是平行四边形,再矩形的判定定理即可得到结论;
(2)由勾股定理得AB=2,再证△ABD∽△BEA,得=,即可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC且AD=BC,
∵CF=BE,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD是矩形;
(2)解:∵CF=BE,CF=2,
∴BE=2,
∵∠AEB=90°,
∴AB===2,
∵AD∥BC,
∴∠BAD=∠EBA,
∵∠AEB=∠ABD=90°,
∴△ABD∽△BEA,
∴=,
即=,
解得:BD=4.
13.(2020春•雨花区校级期末)如图,在▱ABCD中,M、N分别是AD、BC的中点,∠AND=90°,连接CM交DN于点O.
(1)求证:△ABN≌△CDM;
(2)求证:四边形CDMN为菱形;
(3)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求NC的长.
【分析】(1)由四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠B=∠CDM,利用SAS证得△ABN≌△CDM;
(2)利用直角三角形形的性质结合菱形的判定方法证明即可.
(3)易求得∠MND=∠CND=∠2=30°,然后由含30°的直角三角形的性质求解即可求得答案.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,,
∴△ABN≌△CDM(SAS);
(2)证明:∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC∥DM,NC=DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
(3)解:∵M是AD的中点,∠AND=90°,
∴MN=MD=AD,
∴∠1=∠MND,
∵AD∥BC,
∴∠1=∠CND,
∵∠1=∠2,
∴∠MND=∠CND=∠2,
∴PN=PC,
∵CE⊥MN,
∴∠CEN=90°,
∠END+∠CNP+∠2=180°﹣∠CEN=90°,
又∵∠END=∠CNP=∠2,
∴∠2=∠PNE=30°,
∵PE=1,
∴PN=2PE=2,
∴CE=PC+PE=3,
∴NC===2.
14.(2021春•保山期末)如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,OB=OD,点E是BC延长线上一点,连接DE,DE∥AC,DE⊥BD,点D到BE的距离为d.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求d.
【分析】(1)先证四边形ABCD是平行四边形,再证AC⊥BD,即可得出结论;
(2)过点D作DF⊥BE于E,由勾股定理得OB=4,则BD=2OB=8,再证四边形ACED是平行四边形,得DE=AC=6,CE=AD=5,则BE=BC+CE=10,然后由三角形面积即可求解.
【解答】(1)证明:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵DE∥AC,DE⊥BD,
∴AC⊥BD,
∴平行四边形ABCD是菱形;
(2)解:过点D作DF⊥BE于E,如图所示:
由(1)得:OA=AC=3,AC⊥BD,
在Rt△AOB中,由勾股定理得:OB===4,
∴BD=2OB=8,
∵四边形ABCD是菱形,
∴BC=AD=AB=5,AD∥BC,
∵DE∥AC,
∴四边形ACED是平行四边形,
∴DE=AC=6,CE=AD=5,
∴BE=BC+CE=10,
∵DE⊥BD,DF⊥BE,
∴BE×DF=BD×DE,
∴DF===,
即d=.
15.(2021秋•丹东期末)如图,菱形ABCD的对角线AC与BD相交于点O,DE⊥AB于点E交AC于点P,BF⊥CD于点F.
(1)判断四边形DEBF的形状,并说明理由;
(2)如果BE=3,BF=6,求出DP的长.
【分析】(1)根据菱形的性质和矩形的判定解答即可;
(2)根据菱形的性质和矩形的性质得出DE=BF,进而利用勾股定理解答即可.
【解答】(1)解:四边形DEBF是矩形,理由如下:
∵DE⊥AB,BF⊥CD,
∴∠DEB=∠BFD=90°,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠DEB+∠EDF=180°,
∴∠EDF=∠DEB=∠BFD=90°,
∴四边形DEBF是矩形;
(2)解:连接PB,
∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴PB=PD,
由(1)知,四边形DEBF是矩形,
∴DE=FB=6,
设PD=BP=x,则PE=6﹣x,
在Rt△PEB中,由勾股定理得:(6﹣x)2+32=x2,
解得:x=,
∴PD=.
16.(2020•新华区校级一模)如图,在菱形ABCD中,∠ABC=60°,E是CD边上一点,作等边△BEF,连接AF.
(1)求证:CE=AF;
(2)EF与AD交于点P,∠DPE=46°,求∠CBE的度数.
【分析】(1)根据四边形ABCD是菱形,∠ABC=60°和等边△BEF,可以证明△FAB≌△ECB,进而可得CE=AF;
(2)延长FA交BE于点G,结合(1)根据三角形的外角定义可得∠BAD=∠BFE+∠DPE+∠CBE,即可求出∠CBE的度数.
【解答】解:(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
∵△BEF是等边三角形,
∴FB=EB,∠FBE=60°,
∴∠FBE=∠ABC=60°,
∴∠FBA=∠EBC,
∴△FAB≌△ECB(SAS),
∴CE=AF;
(2)∵四边形ABCD是菱形,
∴AD∥BC,
∵∠ABC=60°,
∴∠BAD=120°,
延长FA交BE于点G,
根据三角形的外角定义可知:
∠GAD=∠AFP+∠APF,
∠BAG=∠AFB+∠ABF,
∴∠GAD+∠BAG=∠AFP+∠APF+∠AFB+∠ABF,
∵∠APF=∠DPE=46°,∠ABF=∠CBE,
∴∠BAD=∠BFE+∠DPE+∠CBE,
即120°=60°+46°+∠CBE,
∴∠CBE=14°.
答:∠CBE的度数为14°.
17.(2017秋•莲湖区校级月考)如图,菱形ABCD中,E、F分别是边AD,CD上的两个动点(不与菱形的顶点重合),且满足CF=DE,∠A=60°.
(1)求证:△BEF是等边三角形.
(2)若菱形ABCD的边长为6,当△DEF的面积为时,求DE的长.
【分析】(1)证△BDE≌△BCF(SAS),得∠DBE=∠CBF,BE=BF,证∠EBF=60°,即可得出结论;
(2)作FG作DE于G,由(1)得∠FDG=60°,则∠DFG=30°,由直角三角形的性质得DG=DF,FG=DG=DF,则DF=CD﹣CF=6﹣DE,由△DEF的面积=DE×FG=DE×(6﹣DE)=2,解得DE=2,或DE=4即可.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD=DC=BC=AB,∠A=∠C=60°,
∴△ABD和△BCD都是等边三角形,
∴∠C=∠BDE=60°,BD=BC.
在△BDE和△BCF中,,
∴△BDE≌△BCF(SAS),
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°,
即∠EBF=60°,
∴△BEF是等边三角形;
(2)解:∵菱形ABCD的边长为6,
∴CD=6,
作FG作DE于G,如图2所示:
由(1)得:∠FDG=60°,
∴∠DFG=30°,
∴DG=DF,FG=DG=DF,
∵CF=DE,
∴DF=CD﹣CF=6﹣DE,
∵△DEF的面积=DE×FG=DE×(6﹣DE)=2,
即DE(6﹣DE)=8,
解得:DE=2,或DE=4;
即DE的长为2或4.
18.(2020•渝中区校级二模)如图,四边形ABCD的对角线AC⊥BD于点E,点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.
(1)求证:四边形DBFC是菱形;
(2)若AB=BC,∠F=45°,BD=2,求AC的长.
【分析】(1)证出BD∥CF,CD∥BF,得出四边形DBFC是平行四边形;再证出CD=BD,即可得出结论;
(2)由平行四边形的性质得出CF=BD=2,由等腰三角形的性质得出AE=CE,作CM⊥BF于M,则CE=CM,证出△CFM是等腰直角三角形,得出CM=,则AE=CE=,即可得出AC的长.
【解答】(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴四边形DBFC是菱形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,如图:
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
19.(2020•滦州市二模)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AC=4,AB=5,直接写出菱形ADCF的面积.
【分析】(1)由AAS证明△AEF≌△DEB即可;
(2)由全等三角形的性质得AF=DB,证得四边形ADCF为平行四边形,再利用直角三角形的性质可求得AD=CD,可证得结论;
(3)根据条件可证得S菱形ADCF=S△ABC,再由三角形面积公式可求得答案.
【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
(2)证明:由(1)知,△AFE≌△DBE,
∴AF=DB,
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴,
∴平行四边形ADCF是菱形;
(3)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC=AB•AC=×5×4=10.
20.(2020春•泰兴市校级期末)如图,菱形ABCD中,对角线AC,BD相交于点O,AC=6,BD=18,E,F在对角线BD上.
(1)若BE=DF.
①判断四边形AECF的形状并说明理由;
②若BE=AE,求线段EF的长;
(2)将(1)中的线段EF从当前位置沿射线BD的方向平移,若平移过程中∠EAO=∠EFA,求此时OF的长.
【分析】(1)①证明AC与EF互相垂直平分便可根据菱形的判定定理得出结论;
②设BE=x,在Rt△AOE中,由勾股定理列出x的方程,便可求得结果;
(2)分两种情况:E点在O点左边;E在O点右边.分别通过相似三角形的性质列出OF的方程,进行解答便可.
【解答】解:(1)①四边形AECF是菱形.理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是菱形;
②∵菱形ABCD中,AC=6,BD=18,
∴∠AOC=90°,OA=3,OB=9,
∵BE=AE,
不妨设BE=AE=x,则OE=9﹣x,
在Rt△AOE中,由勾股定理得,32+(9﹣x)2=x2,
解得,x=5,
∴OE=9﹣5=4,
∴EF=2OE=8;
(2)当E点在O点的右边时,如图,
∵∠EAO=∠EFA,∠AOE=∠AOF=90°,
∴△AOE∽△FOA,
∴,
∵OA=3,EF=8,
∴,
解得,OF=4﹣(小于4,不合题意,舍去),或OF=4+,
当点E在O点右边时,如图,
∵∠EAO=∠EFA,∠AOE=∠FOA=90°,
∴△AOE∽△FOA,
∴,即,
解得,OF=﹣1(舍),或OF=9,
综上,OF=9或4+.
21.(2020春•赣州期末)如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;
(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
【分析】(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的周长会随着AE的变化而变化,求出当AE最短时,△CEF的周长即可.
【解答】解:(1)如图,连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠BAC=60°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴BE=CF;
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC=.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+.
22.(2020•衢州模拟)【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是 4 .
【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.
【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连接AD,若AC=3,AD=2,则△ABD的面积是 6 .
【分析】猜想:首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
探究:根据菱形的性质得到AD∥BC,AO=CO=AC=2.5,BO=BD=5,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
应用:延长AC到E使CE=AC=3,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到DE=,即可得到结论.
【解答】解:猜想:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE与△COF中,
,
∴△AEO≌△CFO(AAS),
∴四边形CDEF的面积=S△ACD=▱ABCD的面积=4;
故答案为:4;
探究:∵四边形ABCD是菱形,
∴AD∥BC,AO=CO.
∴∠OAE=∠OCF,∠AEO=∠CFO,
∴在△AOE与△COF中,
,
∴△AOE≌△COF(AAS),
∵由菱形的对称性,得S△ABC=S菱形ABCD,
∴S四边形ABFE=S△ABC=×AC•BD=×5×10=.
应用:延长AC到E使CE=AC=3,
在△ABC与△CDE中,
,
∴△ABC≌△CDE(SAS),
∴∠E=∠BAC=90°,
∴DE=,
∴S△ABD=S△ADE=AE•DE=×6×2=6.
故答案为:6
23.(2020•易门县二模)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数.
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.
【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
24.(2021•西湖区校级三模)如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
【分析】(1)连接BD,由菱形的性质得到AC⊥BD、AB=AD,结合ME⊥AC得到ME∥BD,然后结合点E是AB的中点得到点M时AD的中点,最后得到AM=AE;
(2)①先证明△MAE≌△MDF,然后得到AE=DF=2,进而得到AB的长,最后求得菱形的周长;
②连接CM,记EF与AC交点为点G,先由AM=AE,△MAE≌△MDF得到DF=DM,MF=ME,从而得到∠DMF=∠DFM,进而得到∠ADC=2∠DFM,然后结合∠ADC=2∠MCD得到∠MCD=∠DFM,从而得到MF=MC=ME,∠EMC=2∠FDM=∠MDC,再由ME⊥AC,AM=ME得到∠MGC=90°,ME=2MG,进而得到MC=2MG,即可得到∠MGC=60°,故∠ADC=60°,从而得到△ADC为等边三角形,△DMC为直角三角形,最后求得CM的长即为ME的长.
【解答】(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠FDM=∠MDC,
∵ME⊥AC,AM=AE,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
数学第20章 数据的初步分析综合与测试课后测评: 这是一份数学第20章 数据的初步分析综合与测试课后测评,文件包含专题204数据的初步分析大题专练重难点培优解析版docx、专题204数据的初步分析大题专练重难点培优原卷版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
初中数学沪科版八年级下册19.3 矩形 菱形 正方形课时训练: 这是一份初中数学沪科版八年级下册19.3 矩形 菱形 正方形课时训练,文件包含专题1913正方形的性质与判定大题专练重难点培优解析版docx、专题1913正方形的性质与判定大题专练重难点培优原卷版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
初中数学沪科版八年级下册19.3 矩形 菱形 正方形练习题: 这是一份初中数学沪科版八年级下册19.3 矩形 菱形 正方形练习题,文件包含专题1911矩形的性质与判定大题专练重难点培优解析版docx、专题1911矩形的性质与判定大题专练重难点培优原卷版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。













