人教A版 (2019)3.1 函数的概念及其表示优质第1课时学案及答案

这是一份人教A版 (2019)3.1 函数的概念及其表示优质第1课时学案及答案，共10页。学案主要包含了学习目标，自主学习，小试牛刀，经典例题，跟踪训练，当堂达标，课堂小结，参考答案等内容，欢迎下载使用。
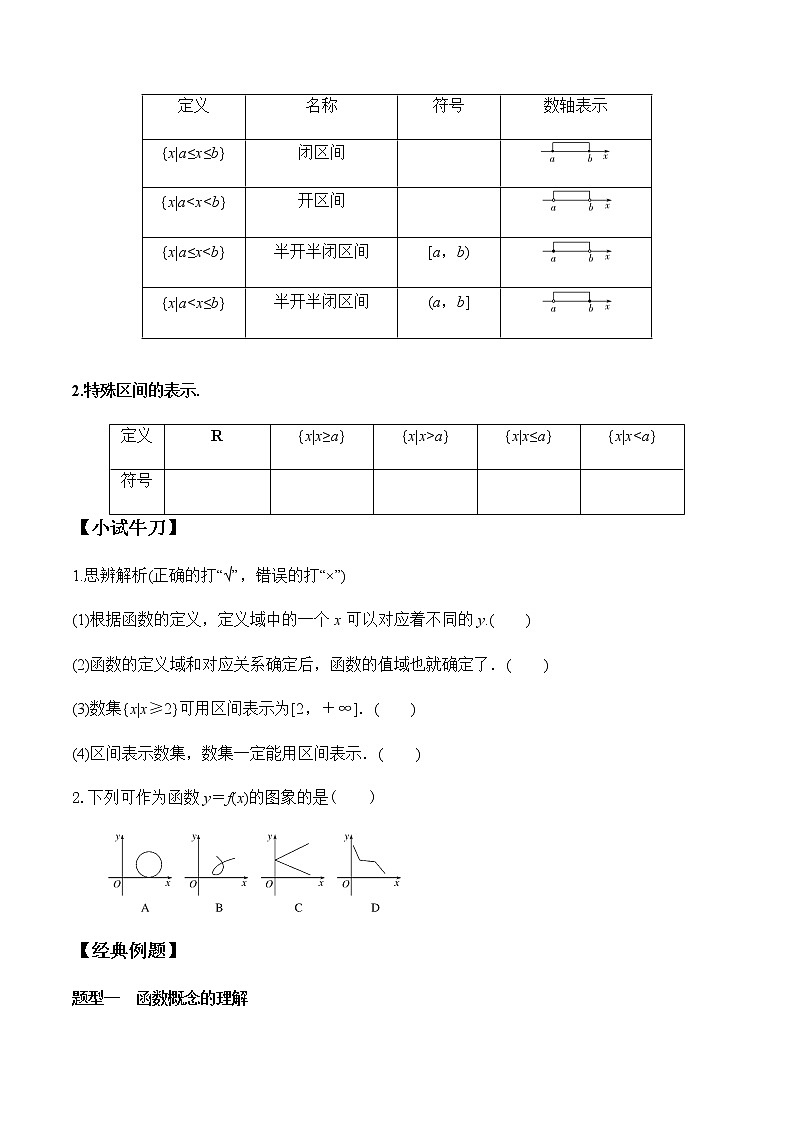
3.1 函数的概念及其表示3.1.1 第1课时 函数的概念（一）【学习目标】课程标准学科素养1.理解函数的概念(重点、难点)；2.会求已知函数的定义域；3.能够正确使用“区间”的符号表示某些集合．1、直观想象2、数学运算3、数学抽象【自主学习】一．    函数的概念概念一般地，设A，B是非空的               ，如果对于集合A中的                         ，按照某种确定的对应关系f，在集合B中都有           确定的数y和它对应，那么就称f：A→B为从集合A到集合B的一个函数三要素对应关系y＝f(x)，x∈A定义域     的取值范围值域与x的值相对应的y的值的集合{f(x)|x∈A}解读：(1)当A，B为非空数集时，符号“f：A→B”表示A到B的一个函数．(2)集合A中的数具有任意性，集合B中的数具有唯一性．(3)符号“f”它表示对应关系，在不同的函数中f的具体含义不一样．二．区间及有关概念1.一般区间的表示.设a，b∈R，且a<b，规定如下：定义名称符号数轴表示{x|a≤x≤b}闭区间 {x|a<x<b}开区间 {x|a≤x<b}半开半闭区间[a，b){x|a<x≤b}半开半闭区间(a，b] 2.特殊区间的表示.定义R{x|x≥a}{x|x>a}{x|x≤a}{x|x<a}符号     【小试牛刀】1.思辨解析(正确的打“√”，错误的打“×”)(1)根据函数的定义，定义域中的一个x可以对应着不同的y.(　　)(2)函数的定义域和对应关系确定后，函数的值域也就确定了．(　　)(3)数集{x|x≥2}可用区间表示为[2，＋∞]．(　　) (4)区间表示数集，数集一定能用区间表示．(    )  2.下列可作为函数y＝f(x)的图象的是(　　)【经典例题】题型一　函数概念的理解点拨：(1)判断对应关系是否为函数的2个条件①A、B必须是非空数集．②A中任意一元素在B中有且只有一个元素与之对应．(2)根据图形判断对应是否为函数的方法①任取一条垂直于x轴的直线l.②在定义域内平行移动直线l.③若l与图形有且只有一个交点，则是函数；若在定义域内没有交点或有两个或两个以上的交点，则不是函数．例1 下列对应为从集合A到集合B的一个函数的是______．(填序号)①A＝R，B＝{x|x>0}，f：x→y＝|x|；②A＝Z，B＝N*，f：x→y＝x2；③A＝Z，B＝Z，f：x→y＝；④A＝[－1,1]，B＝{0}，f：x→y＝0. 【跟踪训练】1  若集合M＝{x|0≤x≤2}，N＝{y|0≤y≤3}，则下列图形给出的对应中能构成从M到N的函数f：M→N的是(　　)    题型二 用区间表示数集 点拨：应用区间时的3个注意点(1)区间是数集，区间的左端点小于右端点．(2)在用区间表示集合时，开和闭不能混淆．(3)用数轴表示区间时，用实心点表示包括在区间内的端点，用空心圈表示不包括在区间内的端点．例2 把下列数集用区间表示：(1){x|x≥－2}； (2){x|x<0}； (3){x|－1<x<1，或2≤x<6}．    【跟踪训练】2 已知区间[－2a,3a＋5]，则a的取值范围为________． 题型三 已知函数的解析式求定义域点拨：求函数定义域的几种类型(1)若f(x)是整式，则函数的定义域是R.(2)若f(x)是分式，则应考虑使分母不为零．(3)若f(x)是偶次根式，则被开方数大于或等于零．(4)若f(x)是由几个式子构成的，则函数的定义域是几个部分定义域的交集．(5)若f(x)是实际情境的解析式，则应符合实际情境，使其有意义．例3求下列函数的定义域．(1)y＝2＋； (2)y＝；  (3)y＝·； (4)y＝(x－1)0＋.  【跟踪训练】3求下列函数的定义域：(1)y＝－.             (2)y＝.   题型四 求抽象函数的定义域点拨：两类抽象函数的定义域的求法(1)已知f(x)的定义域，求f(g(x))的定义域：若f(x)的定义域为[a，b]，则f(g(x))中a≤g(x)≤b，从中解得x的取值集合即为f(g(x))的定义域.(2)已知f(g(x))的定义域，求f(x)的定义域：若f(g(x))的定义域为[a，b]，即a≤x≤b，求得g(x)的取值范围，g(x)的值域即为f(x)的定义域.例4 (1) 已知函数f(x)的定义域为[1,3]，求函数f(2x＋1)的定义域．(2)函数f(2x＋1)的定义域为[1,3]，求函数f(x)的定义域．    【跟踪训练】4 (1)已知函数y＝f(x)的定义域为[－2，3]，求函数y＝f(2x－3)的定义域；(2)已知函数y＝f(2x－3)的定义域是[－2，3]，求函数y＝f(x＋2)的定义域.   【当堂达标】1.（多选）下列图形中， y是x的函数的是(    )2.函数f(x)＝的定义域为(　　)A．{x|－2≤x≤1}   B．{x|－2<x<1}C．{x|－2<x≤1}   D．{x|x≤1}2.已知函数f(x)的定义域是[0,2]，则函数g(x)＝的定义域是(　　)A．[0,1]         B．[0,1)      C．[0,1)∪(1,4]      D．(0,1)3.已知全集U＝R，A＝{x|1<x≤3}，则∁UA用区间表示为________.4.若函数f(x)的定义域是[0,1]，则函数f(2x)＋的定义域为________．6.已知函数y＝的定义域是R，求实数m的取值范围．      【课堂小结】1.函数的本质：两个非空数集间的一种确定的对应关系．由于函数的定义域和对应关系一旦确定，值域随之确定．2.定义域是一个集合，所以需要写成集合的形式，在已知函数解析式又对x没有其他限制时，定义域就是使函数式有意义的x的集合．3.对区间的几点认识(1)区间是集合，是数集，区间的左端点必须小于右端点．(2)用数轴表示区间时，用实心点表示包括在区间内的端点，用空心点表示不包括在区间内的端点．(3)在用区间表示集合时，开和闭不能混淆．(4)“∞”是一个符号，不是一个数，它表示数的变化趋势.          【参考答案】【自主学习】一．实数集   任意一个数x   唯一确定 x 二．1. [a，b]    (a，b)   2.(－∞，＋∞)  [a，＋∞)   (a，＋∞)   (－∞，a]    (－∞，a)【小试牛刀】1.(1)×　 (2)√　　(3)×　(4)×2.D【经典例题】例1 ④ 解析：①中，集合A中的元素0在集合B中没有元素与之对应，②中同样是集合A中的元素0在集合B中没有元素与之对应，对于③，集合A中负整数没有意义．【跟踪训练】1  D 解析：A中的对应不满足函数的存在性，即存在x∈M，但N中无与之对应的y；B、C均不满足函数的唯一性，只有D正确．例2 解：(1){x|x≥－2}用区间表示为[－2，＋∞)；(2){x|x<0}用区间表示为(－∞，0)；(3){x|－1<x<1，或2≤x<6}用区间表示为(－1,1)∪[2,6)．【跟踪训练】2  (－1，＋∞)  解析：由题意可知3a＋5>－2a，解得a>－1.故a的取值范围是(－1，＋∞)．例2 解：(1)当且仅当x－2≠0，即x≠2时，函数y＝2＋有意义，所以这个函数的定义域为{x|x≠2}．(2)要使函数有意义，需x2－2x－3≥0，即(x－3)(x＋1)≥0，所以x≥3或x≤－1，即函数的定义域为{x|x≥3或x≤－1}．(3)函数有意义，当且仅当解得1≤x≤3，所以这个函数的定义域为{x|1≤x≤3}．(4)函数有意义，当且仅当解得x>－1，且x≠1，所以这个函数的定义域为{x|x>－1且x≠1}．【跟踪训练】3  (1)要使函数有意义，自变量x的取值必须满足即即解得－3≤x≤2且x≠－1，即函数定义域为{x|－3≤x≤2且x≠－1}．(2)要使函数有意义，则解得－≤x≤，且x≠±3，即定义域为{x|－≤x≤，且x≠±3}．例4  (1)因为函数f(x)的定义域为[1,3]，即x∈[1,3]，函数f(2x＋1)中2x＋1的范围与函数f(x)中x的范围相同，所以2x＋1∈[1,3]，所以x∈[0,1]，即函数f(2x＋1)的定义域是[0,1]．(2)因为x∈[1,3]，所以2x＋1∈[3,7]，即函数f(x)的定义域是[3,7]．【跟踪训练】4 解：(1)因为函数y＝f(x)的定义域为[－2，3]，即x∈[－2，3]，函数y＝f(2x－3)中2x－3的范围与函数y＝f(x)中x的范围相同，所以－2≤2x－3≤3，解得≤x≤3，所以函数y＝f(2x－3)的定义域为.(2)因为x∈[－2，3]，所以2x－3∈[－7，3]，即函数y＝f(x)的定义域为[－7，3].令－7≤x＋2≤3，解得－9≤x≤1，所以函数y＝f(x＋2)的定义域为[－9，1].【当堂达标】1.ABC 解析：由函数的定义知A，B，C是函数．2.C 解析：要使函数有意义，需解得－2≤x≤1，且x≠－2，所以函数的定义域是{x|－2<x≤1}．3.B 解析：由f(x)的定义域是[0,2]知，，解得0≤x<1，所以g(x)＝的定义域为[0,1)．4.(－∞，1]∪(3，＋∞)解析： ∁UA＝{x|x≤1或x>3}，用区间可表示为(－∞，1]∪(3，＋∞).5. 解析：由得0≤x≤，所以函数f(2x)＋的定义域为.6.解：①当m＝0时，y＝，其定义域是R.②当m≠0时，由定义域为R可知，mx2－6mx＋m＋8≥0对一切实数x均成立，于是有解得0<m≤1.由①②可知，m∈[0,1]．