人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换优秀第2课时学案

这是一份人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换优秀第2课时学案，共16页。学案主要包含了学习目标，自主学习，小试牛刀，经典例题，跟踪训练，当堂达标，参考答案等内容，欢迎下载使用。
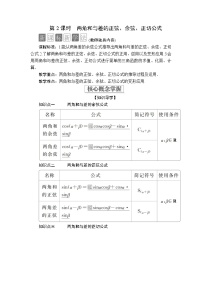
5.5.1 三角恒等变换第2课时  两角和与差的正弦、余弦、正切公式【学习目标】课程标准学科素养1.能根据两角差的余弦公式推导出两角和与差的正弦、正切公式和两角和的余弦公式．2.熟练掌握两角和与差的正弦、余弦、正切公式的特征．3.能灵活运用公式进行化简和求值.1.逻辑推理2.数学运算【自主学习】两角和的余弦公式及两角和与差的正弦、正切公式名称公式简记符号条件两角和的余弦cos(α＋β)＝                    C(α＋β)α，β∈R两角和的正弦sin(α＋β)＝                    S(α＋β)α，β∈R两角差的正弦sin(α－β)＝                    S(α－β)两角和的正切 tan(α＋β)＝                T(α＋β)α，β，α±β≠kπ＋(k∈Z)两角差的正切 tan(α－β)＝                T(α－β)注意：在应用两角和与差的正切公式时，只要tanα，tanβ，tan(α＋β)(或tan(α－β))中任一个的值不存在，就不能使用两角和(或差)的正切公式解决问题，应改用诱导公式或其他方法解题．总结：公式的结构特征和符号规律对于公式 ， ，可记为“余余正正，符号异”.对于公式 ， ，可记为“正余余正，符号同”.对于公式 ， ，可记为“分子同,分母异”.【小试牛刀】1.思考辨析(正确的画“√”，错误的画“×”)(1)把公式cos(α－β)＝cosαcosβ＋sinαsinβ中的β用－β代替，可以得到cos(α＋β)．(　　)(2)两角和与差的正弦、余弦公式中的角α，β是任意的．(　　) (3)对任意的α，β角，都有tan (α±β)＝.(　　) (4)tan能根据公式tan(α＋β)直接展开．(　　)(5)tanα·tanβ，tanα＋tanβ，tan(α＋β)三者知二可表示或求出第三个．(　　)2.cos 75°cos 15°－sin 75°sin 15°的值等于(　　)A.　　    B．－　　　C．0　　　 D．13.若tan α＝3，tan β＝，则tan(α－β)等于(　　)A.         B．－      C．3  D．－34.sin 45°cos 15°－cos 45°sin 15°＝________.【经典例题】题型一  　给角求值　　　　　　　　　　　　　　　　点拨：给角求值问题涉及两角和与差公式的正用和逆用，sin (α＋β) ＝sin αcos β＋cos αsin β即为正用， sin αcos β＋cos αsin β＝sin (α＋β)即为逆用。公式的逆用是三角式变形的重要手段，有时还需把三角函数式的系数0，，，等均可视为某个特殊角的三角函数值，从而将常数换为三角函数使用．例如：cosα－sinα＝sincosα－cossinα＝sin(－α)．注意：在利用两角和差的正切公式时要注意常值代换：如tan＝1，tan＝，tan＝等.还要注意tan＝，tan＝.例1  求下列各式的值： (1) sin 14°cos 16°＋sin 76°cos 74°；(2)sin －cos ；(3).     【跟踪训练】1 求下列各式的值：(1)cos 105°；                   (2)cos75°sin135°＋sin45°cos15°；(3)；              (4).     题型二  给值求值点拨：解题时要注意已知角与所求角之间的关系，恰当地运用拆角、拼角技巧，同时分析角之间的关系，利用角的代换化异角为同角，具体做法是：1.当条件中有两角时，一般把“所求角”表示为已知两角的和或差．角的拆分方式如下：α＝(α＋β)－β＝β－(β－α)，α＝＋，β＝－，2α＝(α＋β)＋(α－β)，2β＝(α＋β)－(α－β)，＋＝＋(α＋β)，＋＝＋(α－β)等.2.当已知角有一个时，可利用诱导公式把所求角转化为已知角．例2 (1) 已知cos α＝，α∈，sin β＝－，β是第三象限角．求sin(α＋β)，sin(α－β)的值；(2)已知sin (＋α)＝，cos (－β)＝，且0<α<<β<，求cos (α＋β)．       【跟踪训练】2 (1)若＝3，tan(α－β)＝2，则tan(β－2α)＝________.(2)已知α∈(0，)，sin (α－)＝，则sinα的值为_________．题型三  给值求角点拨：给值求角的方法一般先求出该角的某个三角函数值，再确定该角的取值范围，最后得出该角的大小．至于求该角的哪一个三角函数值，这要取决于该角的取值范围，然后结合三角函数值在不同象限的符号来确定，一般地，若若角的取值范围是，则选正弦函数、余弦函数均可；若角的取值范围是，则选正弦函数；若角的取值范围是(0，π)，则选余弦函数．例3　(1)已知sinα＝，sinβ＝，且α，β∈(0，)，求角α＋β的大小．(2)若α，β均为锐角，且tanα＝2，tanβ＝3，则α＋β等于(　　)A．       B．      C．        D．【跟踪训练】3 设α，β为钝角，且sinα＝，cosβ＝－，则α＋β的值为(　　)A.         B.         C.         D.或 题型四  正切公式的变形应用点拨：T(α±β)可变形为如下形式：tanα±tanβ＝tan(α±β)(1∓tanαtanβ)；1∓tanαtanβ＝例4  (1)求值：tan 10°＋tan 50°＋tan 10°tan 50°.(2)若锐角α，β满足(1＋tanα)(1＋tanβ)＝4，求α＋β的值．     【跟踪训练】4 在△ABC中，tanA＋tanB＋＝tanAtanB，则C等于(　　)A.           B.          C.         D.【当堂达标】1.已知cosα＝，0＜α＜，则sin (α＋)＝(　　)A．         B．         C．－       D．－2.sin15°－cos15°的值为(　　)A.          B．－       C.           D．－3.在△ABC中，A＝，cosB＝，则sinC等于(　　)A.          B．－      C.         D．－4.已知sinα－cosβ＝，cosα－sinβ＝，则sin(α＋β)＝________.5.计算 (1);(2) tan23°＋tan37°＋tan23°tan37°.  6.已知<α<，0<β<，cos＝－，sin＝，求sin(α＋β)的值．   7.已知：α∈，β∈，且cos(α－β)＝，sinβ＝－，求角α的大小．    8.已知tanα＝2，tanβ＝－，其中0<α<，<β<π.求：(1)tan(α－β)；(2)α＋β的值．                          【参考答案】【自主学习】cosαcosβ－sinαsinβ    sinαcosβ＋cosαsinβ    sinαcosβ－cosαsinβ   【小试牛刀】1. (1)√   (2)√   (3)×   (4)×  (5)√2.C   3.A    4.【经典例题】例1  解：(1)原式＝sin 14°cos 16°＋sin(90°－14°)cos(90°－16°)＝sin 14°cos 16°＋cos 14°sin 16°＝sin(14°＋16°)＝sin 30°＝.(2)原式＝2＝2＝2sin＝－2sin ＝－.(3)原式＝＝tan(45°＋75°)＝tan 120°＝－.【跟踪训练】1  解：(1)原式＝cos(60°＋45°)＝cos 60°cos 45°－sin 60°sin 45°＝×－×＝.(2)原式＝sin15°cos45°＋sin45°cos15°＝sin (15°＋45°)＝sin60°＝.(3)原式＝＝＝＝＝. (4)原式＝＝＝sin 30°＝.例2解：(1)∵cos α＝，α∈，∴sin α＝＝.∵sin β＝－，β是第三象限角，∴cos β＝－＝－.∴sin(α＋β)＝sin αcos β＋cos αsin β＝×＋×＝－.sin(α－β)＝sin αcos β－cos αsin β＝×－×＝.(2)∵0<α<<β<，∴<＋α<π，－<－β<0.又∵sin (＋α)＝，cos (－β)＝，∴cos (＋α)＝－，sin (－β)＝－.∴cos (α＋β)＝sin [＋(α＋β)]＝sin [(＋α)－(－β)]＝sin (＋α)cos (－β)－cos (＋α)sin (－β)＝－(－)×(－)＝－.【跟踪训练】2 (1)  解析：∵＝＝3，∴tanα＝2.又tan(α－β)＝2，∴tan(β－2α)＝tan[(β－α)－α]＝－tan[(α－β)＋α]＝－＝. (2)   解析：由题意可知，因为α∈(0，)，所以α－∈(－)，所以cos (α－)＝＝，则sinα＝sin (α－)＝sin (α－)cos＋cos (α－)sin＝＝.例3　解： (1)∵sinα＝，sinβ＝，且α，β∈(0，)，∴cosα＝＝，cosβ＝＝，∴cos(α＋β)＝cosαcosβ－sinαsinβ＝＝＝＝，又由已知可得α＋β∈(0，π)，∴α＋β＝.(2) B　解析：tan (α＋β)＝＝＝－1.因为α∈(0，)，β∈(0，)，则α＋β∈(0，π)，故α＋β＝.【跟踪训练】3  C解析：∵α，β为钝角，sinα＝，∴cosα＝－＝－＝－，由cosβ＝－，得sinβ＝＝ ＝，∴cos(α＋β)＝cosαcosβ－sinαsinβ＝×－×＝.又∵π<α＋β<2π，∴α＋β＝.故选C.例4 解： (1)∵tan 60°＝tan(10°＋50°)＝，∴tan 10°＋tan 50°＝tan 60°(1－tan 10°tan 50°)，∴原式＝tan 60°(1－tan 10°tan 50°)＋tan 10°tan 50°＝－tan 10°tan 50°＋tan 10°tan 50°＝. (2)∵(1＋tanα)(1＋tanβ)＝1＋(tanα＋tanβ)＋3tanαtanβ＝4，∴tanα＋tanβ＝(1－tanαtanβ)，∴tan(α＋β)＝＝.又∵α，β均为锐角，∴0°<α＋β<180°，∴α＋β＝60°.【跟踪训练】4  A 解析：根据题意可知，tanA＋tanB＝tanAtanB－，所以tan(A＋B)＝＝－因为C＝π－A－B，故tan(A＋B)＝－tanC，所以tanC＝，因为在三角形中0<C<π，故C＝.故选A.【当堂达标】1.B 解析：由cosα＝，0＜α＜，得sinα＝，所以sin (α＋)＝sinα＋cosα＝＝.2.B 解析：原式＝sin30°·sin15°－cos30°·cos15°＝－(cos30°·cos15°－sin30°·sin15°)＝－cos(30°＋15°)＝－cos45°＝－.3.A解析：∵cosB＝，∴B为锐角∴sinB＝＝.又∵sinC＝sin[π－(A＋B)]＝sin(A＋B)＝sincosB＋cossinB＝×＋×＝＝4.   解析：由sinα－cosβ＝两边平方得sin2α－2sinαcosβ＋cos2β＝，①由cosα－sinβ＝两边平方得cos2α－2cosαsinβ＋sin2β＝，②①＋②得：(sin2α＋cos2α)－2(sinαcosβ＋cosαsinβ)＋(cos2β＋sin2β)＝＋.∴1－2sin(α＋β)＋1＝.∴sin(α＋β)＝.5. 解：(1)原式＝＝tan(60°－15°)＝tan45°＝1.(2)∵tan(23°＋37°)＝，∴＝，∴－tan23°tan37°＝tan23°＋tan37°，∴tan23°＋tan37°＋tan23°tan37°＝.6.解：∵<α<，<＋α<π，∴sin＝＝.∵0<β<，<＋β<π，∴cos＝－＝－，∴sin(α＋β)＝－sin(π＋α＋β)＝－sin＝－＝－＝.7.解：因为α∈，β∈，所以α－β∈(0，π)．由cos(α－β)＝，知sin(α－β)＝.由sinβ＝－，知cosβ＝.所以sinα＝sin[(α－β)＋β]＝sin(α－β)cosβ＋cos(α－β)sinβ＝×＋×＝.又α∈，所以α＝.8.解：(1)因为tanα＝2，tanβ＝－，所以tan(α－β)＝＝＝7.(2)因为tan(α＋β)＝＝＝1，又因为0<α<，<β<π，所以<α＋β<，所以α＋β＝.