中考数学复习第18课时全等三角形课堂教学课件

这是一份中考数学复习第18课时全等三角形课堂教学课件，共39页。PPT课件主要包含了要点知识，2已知一边和一角，3已知两角，题串考点，考点2常见模型，平移型，BC＝CE，BC＝EF，轴对称型，公共边BC等内容，欢迎下载使用。

· 考点1 全等三角形基础知识
· 考点2 常见模型
考点1 全等三角形基础知识
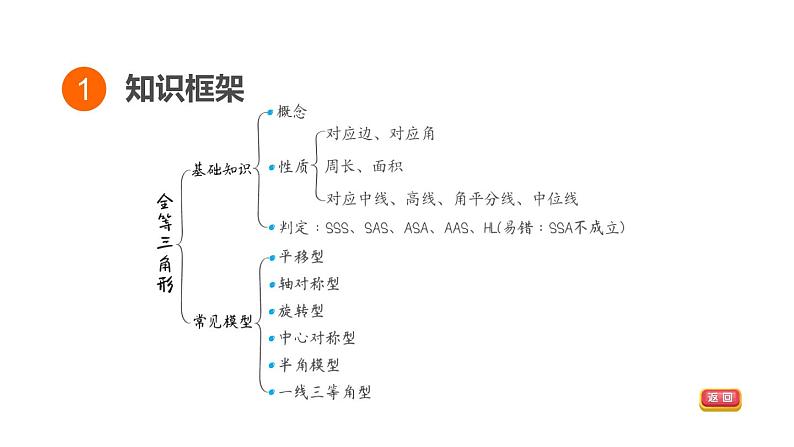
1．全等三角形的性质：(1)对应边相等，对应角相等；(2)周长相等，面积相等；(3)对应的中线、高线、角平分线、中位线都相等．
2．全等三角形的判定思路：
如图，四边形ABCD的对角线AC，BD相交于点O.(1)若AD＝BC，AC＝BD.①求证：∠ADB＝∠BCA；
②求证：△ADO≌△BCO；
(2)若OA＝OB，OC＝OD，求证：△ABC≌△BAD；
(3)若∠ADB＝∠BCA＝90°，AC＝BD，求证：△ABD≌△BAC.
AD＋DC＝DC＋CF
BF＋FC＝FC＋CE
FB＋BE＝BE＋EC
【2017福建8分】如图1，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF.求证：∠A＝∠D.
∠AOC＝∠BOD(对顶角相等)
【2021福建8分】如图2，在△ABC中，D是边BC上的点，DE⊥AC，DF⊥AB，垂足分别为E，F，且DE＝DF，CE＝BF.求证：∠B＝∠C.
【2020福建8分】如图3，点E，F分别在菱形ABCD的边BC，CD上，且BE＝DF.求证：∠BAE＝∠DAF.
如图4，点D是线段CE上一点，且AB＝AC，AD＝AE，∠BAC＝∠DAE.
(1)求证：BD＝CE；
(2)若∠B＝40°，∠E＝80°，求∠CAD的度数．
解：∵△ABD≌△ACE，∴∠B＝∠C＝40°.∵∠E＝80°，∴∠CAE＝180°－∠C－∠E＝60°.∵AD＝AE，∴∠ADE＝∠E，∴∠DAE＝180°－2∠E＝20°，∴∠CAD＝∠CAE－∠DAE＝40°.
【2022福建8分】如图5，点B，F，C，E在同一条直线上，BF＝EC，AB＝DE，∠B＝∠E.求证：∠A＝∠D.
【2018福建8分】如图6，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F.求证：OE＝OF.
【2019福建8分】如图7，点E，F分别是矩形ABCD的边AB，CD上的一点，且DF＝BE.求证：AF＝CE.
如图8，已知△ABC是等边三角形，点D是△ABC外一点，DB＝DC且∠BDC＝120°，∠EDF＝60°，DE，DF分别交AB，AC于点E，F.求证：EF＝BE＋CF.
证明：如图，延长EB至点F′，使得BF′＝CF，连接DF′，∵BD＝DC，∠BDC＝120°，∴∠DBC＝∠DCB＝30°.
∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∴∠ABD＝∠ACD＝90°，∴∠DBF′＝90°＝∠DCF.又∵DB＝DC，BF′＝CF，∴△DBF′≌△DCF(SAS)，∴DF′＝DF，∠BDF′＝∠CDF，∴易得∠EDF′＝∠EDF＝60°，∴△EDF′≌EDF(SAS)，∴EF′＝EF.∵EF′＝BE＋BF′＝BE＋CF，∴EF＝BE＋CF.
证明：∵四边形ABCD为矩形，∴∠B＝∠C＝90°，∴∠BAE＋∠AEB＝90°.∵AE⊥BF，∴∠AEB＋∠CEF＝90°，∴∠BAE＝∠CEF.
如图9，已知矩形ABCD，点E，F分别在BC，CD上，AE⊥EF，且AE＝EF，求证：BE＝CF.
1．如图，点D，E在BC上，△ABE≌△ACD，BC＝10，DE＝4，则BD的长是(　　)A．6 B．5 C．4 D．3
2．如图，△ABC≌△DCB，∠DBC＝35°，则∠AOB的度数为(　　)A．60° B．70° C．80° D．90°
3．【2022成都】如图，在△ABC和△DEF中，点A，E，B，D在同一直线上，AC∥DF，AC＝DF，只添加一个条件，能判定△ABC≌△DEF的是(　　)A．BC＝DE B．AE＝DBC．∠A＝∠DEF D．∠ABC＝∠D
4．如图，△ABC为任意三角形，以AB，AC为边分别向外作等边三角形ABD和等边三角形ACE，连接CD，BE交于点P.求证：(1)CD＝BE；