中考数学复习第28课时对称、折叠课堂教学课件

这是一份中考数学复习第28课时对称、折叠课堂教学课件，共27页。PPT课件主要包含了要点知识，福建6年中考聚焦等内容，欢迎下载使用。

· 考点1 轴对称图形和成轴对称、中心对称图形和成中心对称的识别和性质
· 考点2 最短路径问题
· 考点3 图形的折叠
考点1 轴对称图形和成轴对称、中心对称图形和成中心对称的识别和性质
1．成轴对称的性质：(1)成轴对称的两个图形全等；(2)成轴对称的两个图形中，对应点的连线被对称轴垂直平分．
2．成中心对称的性质：(1)成中心对称的两个图形是全等形；(2)成中心对称的两个图形中，对应点的连线经过对称中心，且被对称中心平分．3．常见的既是轴对称图形又是中心对称图形的有：线段、矩形、菱形、正方形、正六边形、圆等．
1．【2022福建4分】美术老师让同学们设计窗花，下列作品为轴对称图形的是(　　)
福建6年中考聚焦[6年4考]
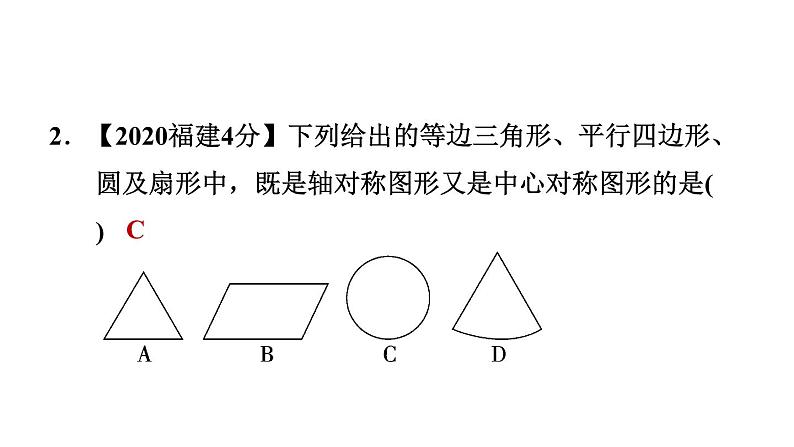
2．【2020福建4分】下列给出的等边三角形、平行四边形、圆及扇形中，既是轴对称图形又是中心对称图形的是(　　)
3．【2019福建4分】下列图形中，既是轴对称图形又是中心对称图形的是(　　)A．等边三角形 B．直角三角形C．平行四边形 D．正方形
4．【2017福建4分】下列关于图形对称性的命题中，正确的是(　　)A．圆既是轴对称图形，又是中心对称图形B．正三角形既是轴对称图形，又是中心对称图形C．线段是轴对称图形，但不是中心对称图形D．菱形是中心对称图形，但不是轴对称图形
考点2 最短路径问题
1．思想方法：利用轴对称将最短路径问题转化为“两点之间，线段最短”问题．
2．最短路径问题的基本图形：
1．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC＋PQ的最小值是(　　)A. B．4 C. D．5
2．如图，四边形ABCD是菱形，对角线AC，BD相交于点O，AC＝6 ，BD＝6，点P是AC上一动点，点E是AB的中点，则PD＋PE的最小值为________．
考点3 图形的折叠
折叠的性质：(1)位于折痕两侧的图形关于折痕对称；(2)折叠前后的两部分图形全等，对应边、角、线段、周长、面积均相等；(3)折叠前后，对应点的连线被对称轴垂直平分．
1．【2022宁德一模4分】如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE＝3，则sin∠BFD的值为(　　)
福建6年中考聚焦[6年2考]
2．【2022宁德一模4分】如图，在四边形纸片ABCD中，AD∥BC，AB＝10，∠B＝60°，将纸片折叠，使点B落在AD边上的点G处，折痕为EF，若∠BFE＝45°，则BF的长为________．
1．【2022龙岩质检4分】下列标志中，既是轴对称图形又是中心对称图形的是(　　)
2．已知点P为∠O内一定点，分别在∠O的两边上找点A，B，使△PAB的周长最小的是(　　)
3．如图，△ABC和△A′B′C′关于直线l对称，下列结论：(1)△ABC≌△A′B′C′；(2)∠BAC＝∠B′A′C′；(3)若连接CC′，则直线l垂直平分CC′；(4)直线l平分∠CAC′.其中正确的有(　　)A．1个 B．2个 C．3个 D．4个
4．【2022大庆】如图，将平行四边形ABCD沿对角线BD折叠，使点A落在E处．若∠1＝56°，∠2＝42°，则∠A的度数为(　　)A．108° B．109° C．110° D．111°
5．如图，△ABC和△DEC关于点C成中心对称，若AC＝ ，AB＝1，∠BAC＝90°，则AE的长是________．
6．如图所示，在正方形网格中，每个小正方形的边长为1个单位．(1)以直线m为对称轴作四边形ABCD的对称图形；