中考数学复习第41课时二次函数与其他几何图形的综合应用课后练课件

这是一份中考数学复习第41课时二次函数与其他几何图形的综合应用课后练课件，共32页。PPT课件主要包含了思路导航等内容，欢迎下载使用。

1．【2022厦门模拟14分】在平面直角坐标系中，已知抛物线y＝ax2＋bx＋6(a≠0)过点A(－2，0)，B(3，0)，与y轴的交点为C.(1)求抛物线的解析式；
解：由题意可设抛物线的解析式为y＝a(x－3)(x＋2)，即y＝a(x2－x－6)＝ax2－ax－6a，∴－6a＝6，解得a＝－1.∴抛物线的解析式为y＝－x2＋x＋6.
1．【2022厦门模拟14分】在平面直角坐标系中，已知抛物线y＝ax2＋bx＋6(a≠0)过点A(－2，0)，B(3，0)，与y轴的交点为C.(2)若点C关于x轴的对称点为D，该抛物线上是否存在点P，使得以点A，B，D，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；
解：存在．对于y＝－x2＋x＋6，令x＝0，则y＝6，故C(0，6)．∵点C关于x轴的对称点为D，∴D(0，－6)，以点A，B，D，P为顶点的四边形是平行四边形，分以下两种情况：①当AB是边时，则DP∥AB且DP＝AB＝5，∴点P的坐标为(5，－6)或(－5，－6)，当x＝5时，y＝－x2＋x＋6＝－14≠－6，
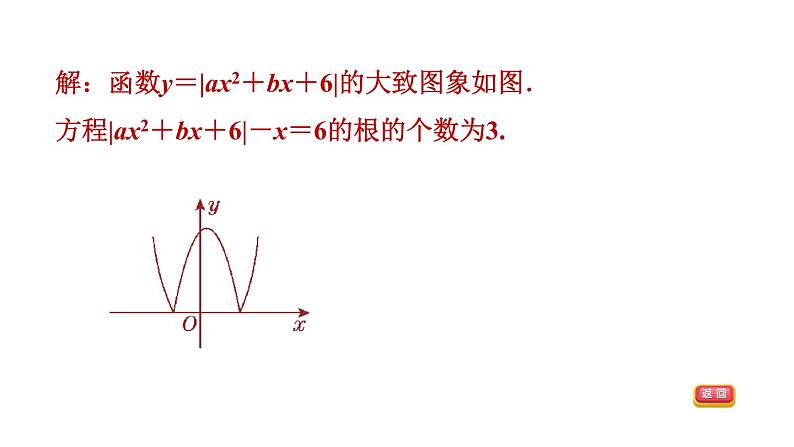
1．【2022厦门模拟14分】在平面直角坐标系中，已知抛物线y＝ax2＋bx＋6(a≠0)过点A(－2，0)，B(3，0)，与y轴的交点为C.(3)试画出函数y＝|ax2＋bx＋6|的大致图象，并直接写出方程|ax2＋bx＋6|－x＝6的根的个数．
解：函数y＝|ax2＋bx＋6|的大致图象如图．方程|ax2＋bx＋6|－x＝6的根的个数为3.
2. 已知抛物线y＝x2＋bx＋c与x轴交于A(x1，0)，B(x2，0)两点(x1＜x2)．(1)若b＝2，c＝－5，求AB的长；
2. 已知抛物线y＝x2＋bx＋c与x轴交于A(x1，0)，B(x2，0)两点(x1＜x2)．(2)点C(m，n)在点A，B间的抛物线上(不含点A，B)，若∠ACB＝90°.①求n的值；
解：对于y＝x2＋bx＋c，当y＝0时，x2＋bx＋c＝0，则易得x1＋x2＝－b，x1x2＝c，∵点C在抛物线y＝x2＋bx＋c上，∴n＝m2＋bm＋c.如图，过点C作CE⊥x轴于点E，则∠ECB＋∠EBC＝90°.∵∠ACB＝90°，∴∠ACE＋∠ECB＝90°，∴∠ACE＝∠EBC，
2. 已知抛物线y＝x2＋bx＋c与x轴交于A(x1，0)，B(x2，0)两点(x1＜x2)．(2)点C(m，n)在点A，B间的抛物线上(不含点A，B)，若∠ACB＝90°.②以AC，BC为边作矩形ACBD，当点D落在直线x＝2上，且矩形ACBD的面积最小时，求抛物线的解析式．
∴(x2－x1)2＝(x2＋x1)2－4x1x2＝b2－4c＝b2－4(－2b－5)＝b2＋8b＋20＝(b＋4)2＋4.∵1＞0，∴当b＝－4时，(x2－x1)2的值最小，即此时矩形ACBD的面积最小，c＝－2b－5＝3，∴此时抛物线的解析式为y＝x2－4x＋3.
3.如图，已知直线y＝ x＋4与x轴交于点A，与y轴交于点C.抛物线y＝ax2＋bx＋c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝－1.(1)求抛物线的解析式；
3.如图，已知直线y＝ x＋4与x轴交于点A，与y轴交于点C.抛物线y＝ax2＋bx＋c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝－1.(2)D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时点D的坐标；
3.如图，已知直线y＝ x＋4与x轴交于点A，与y轴交于点C.抛物线y＝ax2＋bx＋c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝－1.(3)若点P在抛物线对称轴上，是否存在点P，Q，使以A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
4. 抛物线y＝－ x2＋ x－1与x轴交于点A，B(点A在点B的左侧)，与y轴交于点C，其顶点为D.将抛物线位于直线l：y＝t(t＜ )上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．
(1)点A，B，D的坐标分别为_______，________，________；
(2)如图①，抛物线翻折后，点D落在点E处，连接AC，BC.当点E在△ABC内(含边界)时，求t的取值范围；
(3)如图②，当t＝0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．