2020-2021学年5.3.2 事件之间的关系与运算教课ppt课件

这是一份2020-2021学年5.3.2 事件之间的关系与运算教课ppt课件，共36页。PPT课件主要包含了学习目标，一定发生，图5-3-2，和或并，图5-3-3，公共样本点，互斥事件，图5-3-4，对立事件，图5-3-5等内容，欢迎下载使用。

1.了解事件间的包含关系和相等关系, 理解互斥事件与对立事件的概念与关系；
2.会用互斥事件与对立事件的概率公式求概率, 了解并事件与交事件的概念,会进行事件的运算.
◆ 知识点一 事件的包含与相等
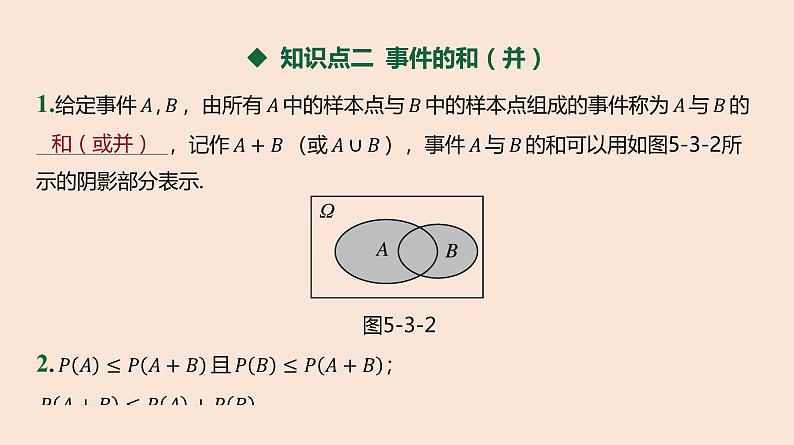
◆ 知识点二 事件的和（并）
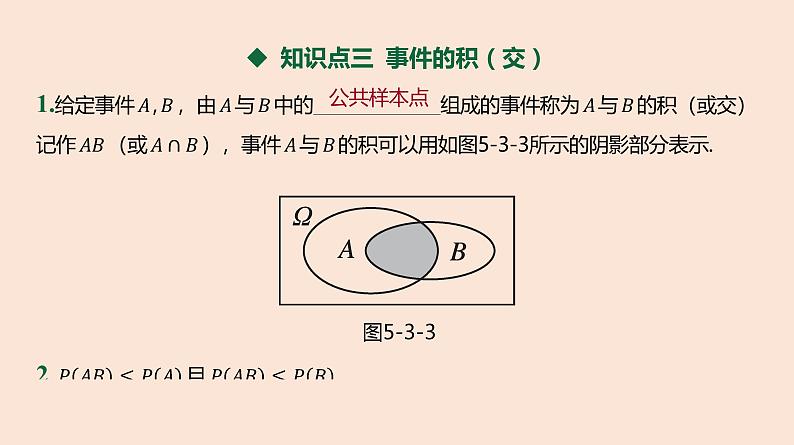
◆ 知识点三 事件的积（交）
◆ 知识点四 事件的互斥与对立
3.概率的几个基本性质
（1） 概率的取值范围：_______.
（2） 必然事件发生的概率为____，不可能事件发生的概率为____.
【诊断分析】 判断正误.（请在括号中打“√”或“×”）
（1） 对立事件一定互斥.( )
（2） 互斥事件是指两个事件在一次试验中不会同时发生，但可以同时不发生. ( )
◆ 知识点五 事件的混合运算
同数的加、减、乘、除混合运算一样，事件的混合运算也有优先级，我们规定：求积运算的优先级高于求和运算.
◆ 探究点一 事件的包含与相等
◆ 探究点二 交事件与并事件
[素养小结]进行事件的运算时，一是要紧扣运算的定义，二是要全面考虑同一条件下的试验可能出现的全部结果，必要时可列出全部的试验结果进行分析，也可类比集合的关系和运算用维恩图分析事件.
◆ 探究点三 互斥事件与对立事件
解：不能.因为甲命中目标与乙命中目标两事件不互斥.
[答案] 能.因为命中靶的内圈和命中靶的其余部分是互斥事件.
[答案] 不对.因为“不出现正面向上”与“同时出现正面向上”不是对立事件，故其概率之和不为1.
变式.某服务电话，打进的电话响第1声时被接的概率是0.1；响第2声时被接的概率是0.2；响第3声时被接的概率是0.3；响第4声时被接的概率是0.35．
（1） 打进的电话在响5声之前被接的概率是多少？
（2） 打进的电话响4声而不被接的概率是多少？
（1）判断两个事件是否互斥,主要看它们在一次试验中能否同时发生,若不能同时发生,则这两个事件互斥,否则不互斥.
（2）判断两个事件是否对立,主要看在一次试验中这两个事件是否同时满足两个条件:一是不能同时发生;二是必有一个发生.
◆ 探究点四 事件的混合运算
（1） 求“取出1个球为红球或黑球”的概率；
（2） 求“取出1个球为红球或黑球或白球”的概率．
（1） 2次都抽到红球；
（2） 第1次抽到红球，第2次抽到白球；
（3） 至少有1次抽到红球.
[素养小结]事件混合运算的关键是搞清楚事件之间的关系,正确地选择计算事件概率的公式.
1.互斥事件与对立事件辨析
例1 判断下列各对事件是否为互斥事件,是否为对立事件.并说明理由.某小组有3名男生和2名女生,从中任选2名学生去参加演讲比赛,其中:
（1） 恰有1名男生和恰有2名男生;
解：是互斥事件,不是对立事件.理由:在所选的2名学生中,“恰有1名男生”实质是“1名男生和1名女生”,它与“恰有2名男生”不可能同时发生,所以是一对互斥事件,但其并事件不是必然事件,所以不是对立事件.
[分析]根据互斥事件、对立事件的定义判断.
（2） 至少有1名男生和至少有1名女生;
[答案] 不是互斥事件,也不是对立事件.理由:“至少有1名男生”包括“1名男生、1名女生”和“2名男生”两种结果,“至少有1名女生”包括“1名女生、1名男生”和“2名女生”两种结果,它们可同时发生.
（3） 至少有1名男生和全是男生;
[答案] 不是互斥事件,也不是对立事件.理由:“至少有1名男生”包括“1名男生、1名女生”和“2名男生”,这与“全是男生”可同时发生.
（4） 至少有1名男生和全是女生.
[答案] 是互斥事件,也是对立事件.理由:“至少有1名男生”包括“1名男生、1名女生”和“2名男生”两种结果,它与“全是女生”不可能同时发生,且其并事件是必然事件,所以是对立事件.对立事件一定是互斥事件,也就是说不互斥的两个事件一定不是对立事件,在确定了两个事件互斥的情况下,就要看这两个事件的和是否为必然事件,这是判断两个事件对立的基本方法.
（1）运用互斥事件的概率加法公式解题的步骤:①确定题中哪些事件彼此互斥;②将待求事件拆分为几个互斥事件之和;③先求各互斥事件分别发生的概率,再求和.
（1） 求他乘火车或乘飞机去的概率.
（2） 求他不乘轮船去的概率.
（3） 如果他选择某种出行方式的概率为0.5,那么这种出行方式可以是什么?