浙教版九年级下册2.2 切线长定理课时作业

这是一份浙教版九年级下册2.2 切线长定理课时作业，共13页。试卷主要包含了2切线长定理，5B．2C．2D．3等内容，欢迎下载使用。
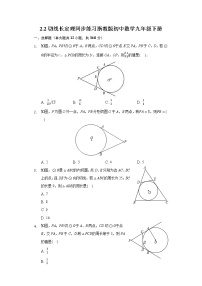
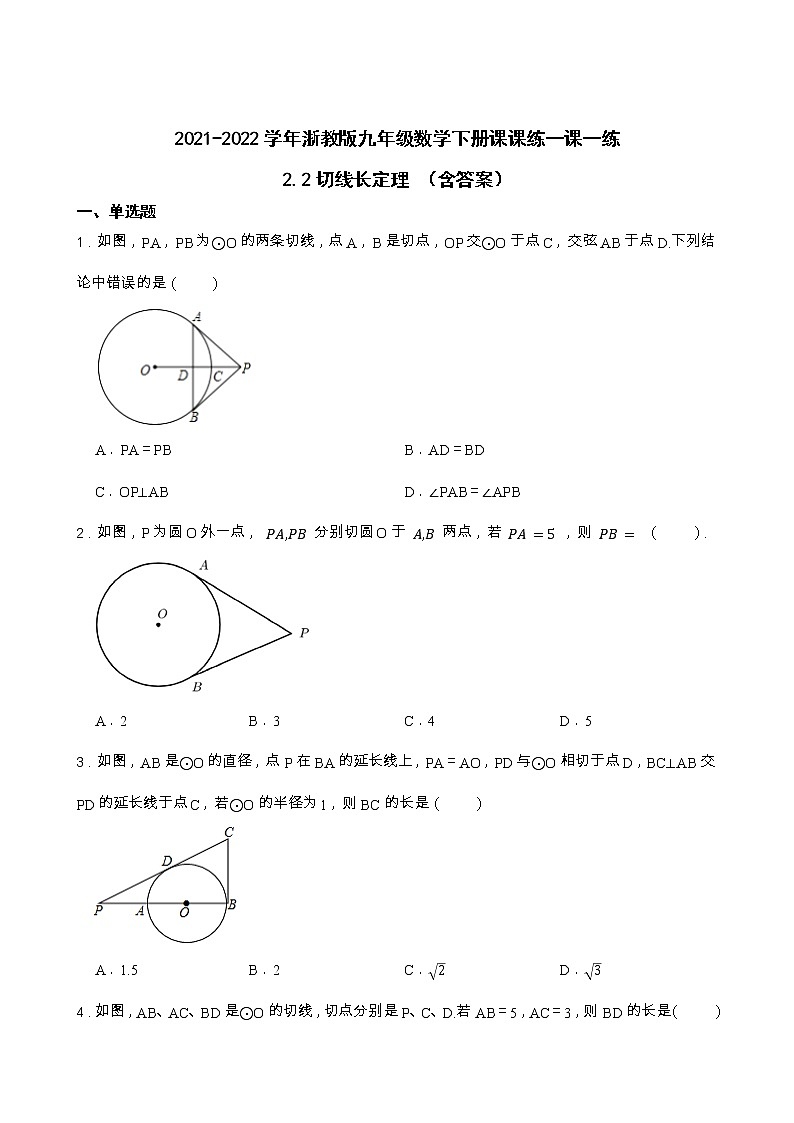
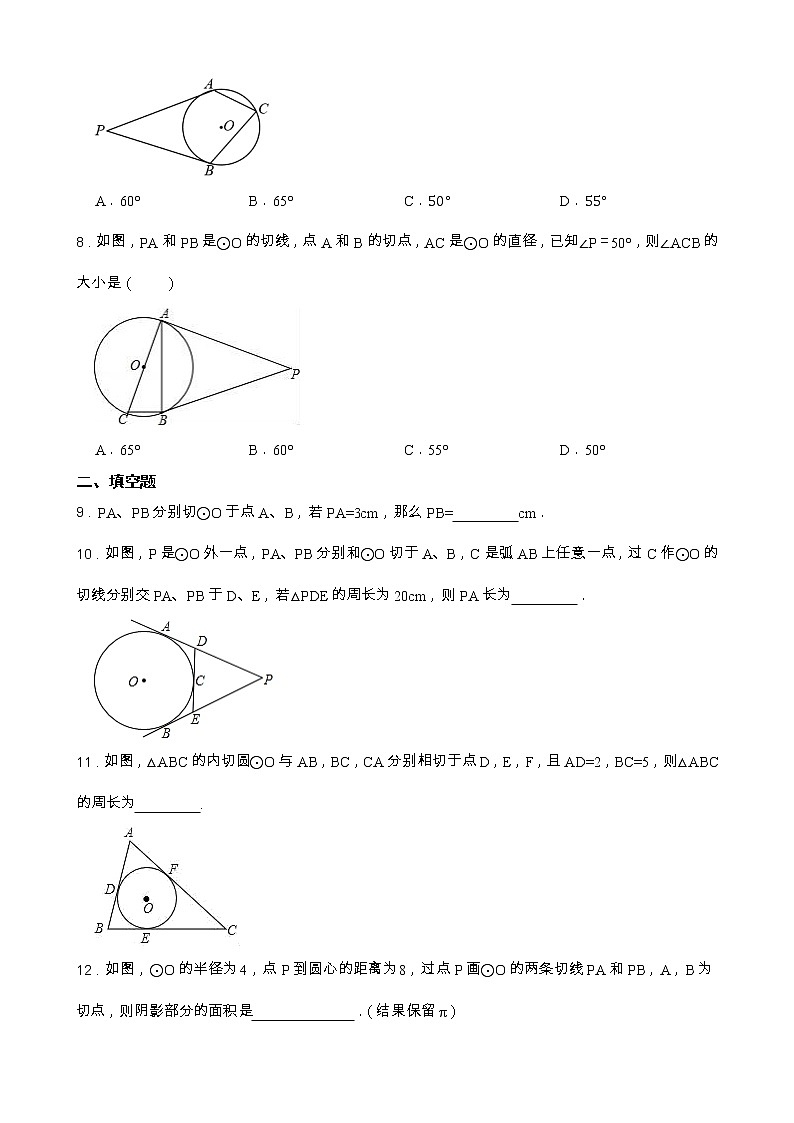
 2021-2022学年浙教版九年级数学下册课课练一课一练2.2切线长定理 （含答案）一、单选题1．如图，PA，PB为⊙O的两条切线，点A，B是切点，OP交⊙O于点C，交弦AB于点D.下列结论中错误的是（　　）  A．PA＝PB B．AD＝BDC．OP⊥AB D．∠PAB＝∠APB2．如图，P为圆O外一点， 分别切圆O于 两点，若 ，则 （　　）.  A．2 B．3 C．4 D．53．如图，AB是⊙O的直径，点P在BA的延长线上，PA＝AO，PD与⊙O相切于点D，BC⊥AB交PD的延长线于点C，若⊙O的半径为1，则BC的长是（　　）A．1.5 B．2 C． D．4．如图，AB、AC、BD是⊙O的切线，切点分别是P、C、D.若AB＝5，AC＝3，则BD的长是（　　）  A．4 B．3 C．2 D．15．下列命题中，正确有（　　）  ①平分弦的直径垂直于弦；②三角形的三个顶点确定一个圆；③圆内接四边形的对角相等；④圆的切线垂直于过切点的半径；⑤过圆外一点所画的圆的两条切线长相等．A．1个 B．2个 C．3个 D．4个6．如图，△ABC是一张周长为18cm的三角形纸片，BC=5cm，⊙O是它的内切圆，小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为(　　)
 A．13cm B．8cmC．6．5cm D．随直线MN的变化而变化7．如图PA、PB分别与⊙O相切于A．B两点，点C为⊙O上一点，连接AC．BC，若∠ACB=60°，则 的度数为（　　）A．60° B．65° C． D．8．如图，PA和PB是⊙O的切线，点A和B的切点，AC是⊙O的直径，已知∠P＝50°，则∠ACB的大小是（　　）  A．65° B．60° C．55° D．50°二、填空题9．PA、PB分别切⊙O于点A、B，若PA=3cm，那么PB=　     　cm．10．如图，P是⊙O外一点，PA、PB分别和⊙O切于A、B，C是弧AB上任意一点，过C作⊙O的切线分别交PA、PB于D、E，若△PDE的周长为20cm，则PA长为　     　．11．如图，△ABC的内切圆⊙O与AB，BC，CA分别相切于点D，E，F，且AD=2，BC=5，则△ABC的周长为　     　.12．如图，⊙O的半径为4，点P到圆心的距离为8，过点P画⊙O的两条切线PA和PB，A，B为切点，则阴影部分的面积是　          　．（结果保留π）13．如图，AB、AC、BD是⊙O的切线，P、C、D为切点，如果AB＝5，AC＝3，则BD的长为　     　．14．如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=60°，则∠P=　     　度． 15．如图，PA，PB分别切⊙O于A，B，并与⊙O的切线，分别相交于C，D，已知△PCD的周长等于10cm，则PA=　     　cm．三、解答题16．如图， 和 是⊙ 的两条切线，A，B是切点．C是 上任意一点，过点C画⊙ 的切线，分别交 和 于D，E两点，已知 ，求 的周长．    17．如图， ， 分别与 相切于 两点，若 ，求 的度数．   18．如图所示， 分别切 的三边 、 、 于点 、 、 ，若 ， ， ．  （1）求 的长；   （2）求 的半径长．      19．已知：如图， 分别切 于点 点．  （1）若 ，求 ；   （2）若 ，求 的周长．          四、综合题20．如图，△ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．（1）求证：∠ACD= ∠B；  （2）若BC＝6，AC＝8，求AD和CD的长． 21．如图，AB，BC，CD分别与⊙O相切于E，F，G，且AB CD，BO＝6cm．CO＝8cm，  （1）求证：BO⊥CO；（2）求⊙O的半径．
答案解析部分1．D2．D3．D4．C5．C6．B7．A8．A9．310．10cm11．1412．13．214．6015．516．解：∵DA、DC是圆O的切线， ∴DA=DC，同理可得EC=EB，∴C△PDE=PD+PE+DE=PD+PE+DC+CE=PD+PE+DA+EB=PA+PB=10cm．17．解： 、 是 切线，  ， ， ， ， ， ， ， ．18．（1）解：设  ，     分别切    的三边  、 、   于点  、 、 ， ， ， ， ， ， ， ，即  ，得  ，  的长为  （2）解：如图，连接OD、OE、OF、OA、OB、OC，  则OD⊥AB,OE⊥BC,OF⊥AC,且OD=OE=OF=2，∵ ， ， ,∴AB2+BC2=AC2，∴△ABC是直角三角形，且∠B是直角，∴△ABC的面积= ,∴ ,∴OD=2,即 的半径长为2.19．（1）解：连接OA、OB和OE  ∵点A和点B均为圆O的切点∴∠PAO=∠PBO =90°∴∠AOB=360°-∠P-∠PAO-∠PBO=140°又CA和CE均为圆的切线∴∠ACO=∠ECO，∠OAC=∠OEC=90°∴∠AOC=∠EOC= 同理可得∠EOD= ∠EOB∴∠COD=∠EOC+∠EOD= =70°（2）解：∵PA、PB和CD分别切圆O于点A、B和E点  ∴CE=CA，DE=DB，PA=PB∴△PCD的周长=PC+PD+CD=PC+AC+PD+DB=PA+PB=2PA=20cm20．（1）证明：如图，连接OD. ∵AB为切线，∴OD⊥AB，∴∠ODB＝90°.∵∠ACB＝90°，∴∠ABC+∠COD＝180°.∵∠AOD+∠COD＝180°，∴∠AOD＝∠ABC.∵∠AOD＝2∠ACD，∴∠ACD= ∠ABC.（2）解：在Rt△ABC中，AB= ∵OC⊥CB，∴BC为切线，∴BD＝BC＝6，∴AD＝4.设⊙O的半径为r，则OD＝OC＝r，OA＝8﹣r，在Rt△AOD中，r2+42＝（8﹣r）2，解得r＝3，∴OC＝3.如图，连接OB交CD于H.∵OC＝OD，BC＝BD，∴OB垂直平分CD.在Rt△OCB中，OB= ∴CD＝2CH= 21．（1）证明：连接OF；根据切线长定理得：BE＝BF，CF＝CG，∠OBF＝∠OBE，∠OCF＝∠OCG； ∵AB CD，∴∠ABC+∠BCD＝180°，∴∠OBE+∠OCF＝90°，∴∠BOC＝90°，∴BO⊥CO；（2）解：由（1）知，∠BOC＝90°． ∵OB＝6cm，OC＝8cm，∴由勾股定理得到：BC＝ ＝10cm，∵OF⊥BC，∴OF＝ ＝4.8cm．