初中数学第6章 图形的相似6.7用相似三角形解决问题教学ppt课件

这是一份初中数学第6章 图形的相似6.7用相似三角形解决问题教学ppt课件，共33页。PPT课件主要包含了情景导入，平行投影及应用，中心投影及应用，∴CD16m等内容，欢迎下载使用。

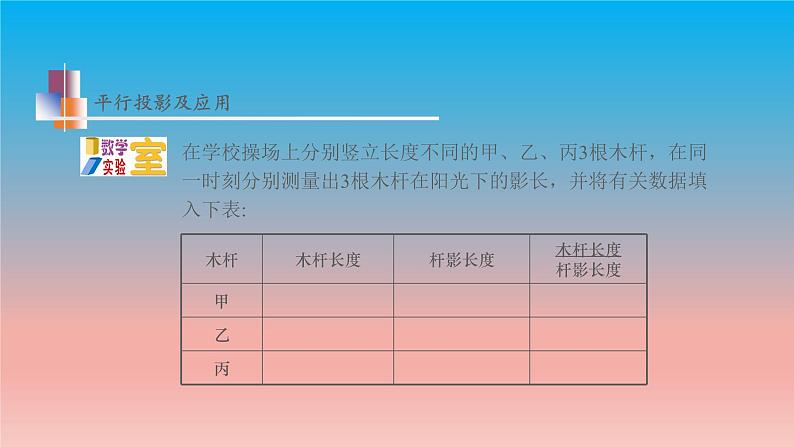
怎样才能测出金字塔的高度？
埃及金字塔始建于公元前2600年以前，目前有96座金字塔. 大部分位于开罗西南部的吉萨高原的沙漠中，是世界公认的“古代世界八大奇迹”之一. 塔内有甬道、石阶、墓室、木乃伊也就是法老的尸体等。最大、最有名的是祖孙三代金字塔——胡夫金字塔、哈夫拉金字塔和门卡乌拉金字塔（孟卡拉金字塔)，其中以胡夫金字塔最为出名.埃及金字塔成为了古埃及文明最具有影响力和持久力的象征.
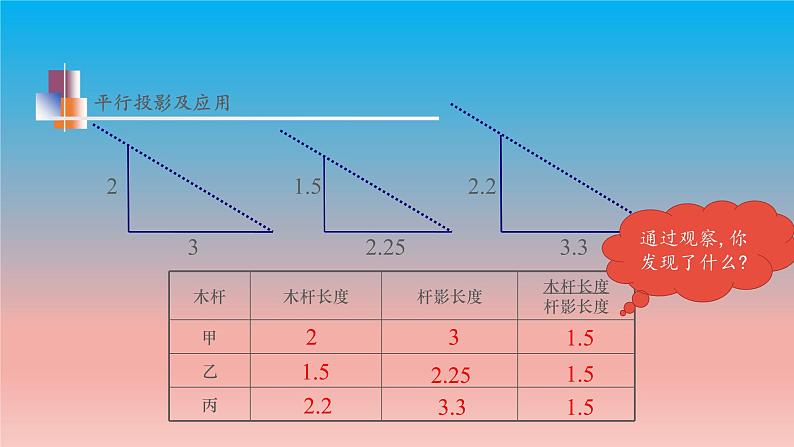
通过观察,你发现了什么?
你能说出其中的缘由吗？
如图，AC是金字塔的高，如果此时测得金字塔的影DB的长为32 m，金字塔底部正方形的边长为230 m，你能计算这座金字塔的高度吗？
你能用这种方法测量出学校附近某一物体的高度吗？
在点光源的照射下，物高与影长一般不成比例.
【分析】由△ABF∽△CDF，CD、DF是已知量，可以得到AB与BF(BD)之间的一个关系式；△ABG∽△EFG，且EF，FG是已知量，可以得到AB与BG(BD)之间的又一个关系式. 这样，根据这两个关系式可以求得BD和AB.
用相似三角形测量高度或者宽度
解：由题意，得∠APB=∠CPD.
∵AB⊥BD，CD⊥BD，
∴∠ABP=∠CDP=90°，
∴△ABP∽△CDP，
答：CD的高度为16 m.
解：∵∠PQR =∠PST =90°，∠P=∠P，
∴△PQR∽△PST.
∴PQ×90 = (PQ+45)×60.
因此，河宽大约为 90 m.
解得 PQ = 90.
1.在下面的图形中，表示两棵小树在同一时刻阳光下的影子的是 ( )
2.兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为l米的竹竿的影长为0.4 m，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得该影子的长为0.2 m，一级台阶高为0.3 m，如图所示，若此时落在地面上的影长为4.4 m，则树高为 ( )A．11.5 m B．11.75 m C．11.8 m D．12.25 m
3.如图，小强晚上在路灯下散步，在由A处走到B处这一过程中，他在地上的影子( )A．逐渐变短 B．逐渐变长 C．先变短后变长 D．先变长后变短
4.小华同学自制了一个简易的幻灯机，其工作情况如图所示，幻灯片与屏幕平行，光源到幻灯片的距离是30 cm，幻灯片到屏幕的距离是1.5 m，幻灯片上小树的高度是10 cm，则屏幕上小树的高度是 ( ) A．50m B．500 cm C．60 cm D．600 cm
5.墨子是春秋战国时期墨家学派的创始人，著名思想家、教育家、科学家、军事家.墨子曾和他的学生做过小孔成像的实验．他的做法是，在一间黑暗的屋子里，一面墙上开一个小孔，小孔对面的墙上就会出现外面景物的倒像．小华在学习了小孔成像的原理后，利用如图所示的装置来验证小孔成像的现象．已知一根点燃的蜡烛距小孔20 cm，光屏在距小孔30 cm处，小华测量了蜡烛的火焰高度为2 cm，则光屏上火焰所成像的高度为________cm.
6.如图，阳光通过窗口照到教室内，竖直窗框在地面上留下2.1 m长的影子如图所示，已知窗框的影子DE到窗下墙脚的距离CE=3.9 m，窗口底边离地面的距离BC=1.2 m，试求窗口的高度．（即AB的值）
解：∵阳光是平行光线，即AE∥BD ，
∴△AEC∽△BDC.
又∵AC=AB+BC，DC=EC-ED，EC=3.9， ED=2.1，BC=1.2，
解得AB= 1.4(m).