北京景山学校2022_2023学年七年级上学期 期中数学试卷

这是一份北京景山学校2022_2023学年七年级上学期 期中数学试卷，共9页。
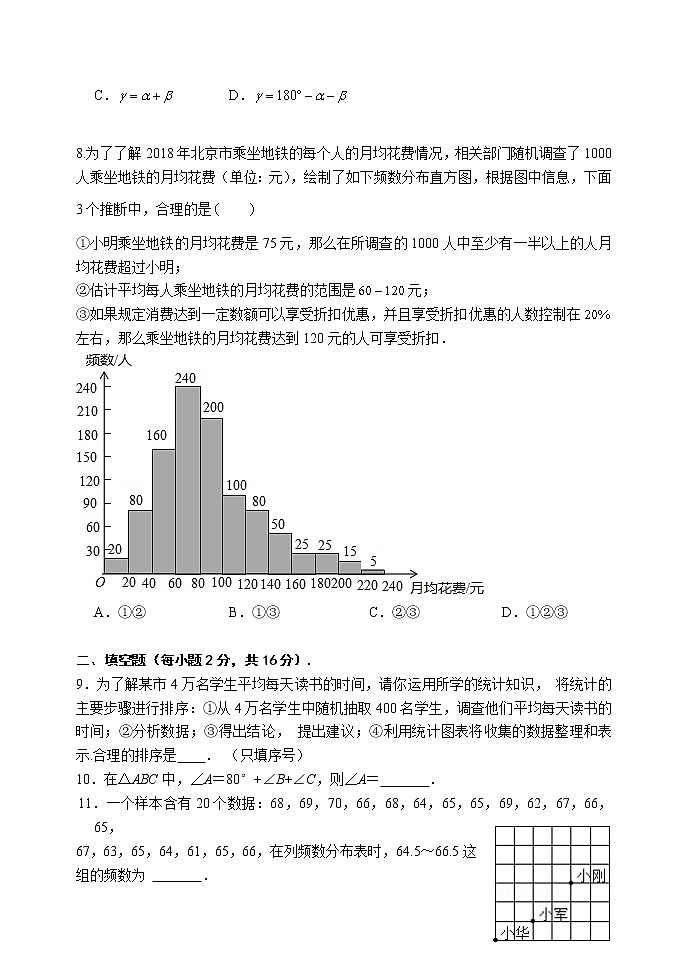
北京景山学校2022～2023学年度第一学期七 年 级 数 学 期 中 试 卷班级______  姓名           学号           成绩            注 意事 项（1）请用黑色钢笔或签字笔答题，不得使用铅笔或红笔答卷。（2）认真审题，字迹工整，卷面整洁。（3）本试卷共8页，共有三道大题，28道小题，考试时间100分钟。（4）请将选择题的答案填涂在机读卡上，其余试题答案填写在答题纸上。一、选择题（每题只有一个选项符合题意，每小题2分，共16分）.1.只有一条高在三角形内部的三角形是（　　）A．锐角三角形                  B．直角三角形 C．钝角三角形                      D．直角三角形或钝角三角形2. 若点P（x,y）的坐标满足=0，则点P 的位置是（    ）A. 在x轴上                       B．在y轴上 C．是坐标原点                     D．在x轴上或在y轴上3. 2021年某市有5.6万学生参加联招考试，为了了解他们的数学成绩，从中抽取2000名考生的数学成绩进行统计分析，下列说法错误的是（　　）A．这种调查方式是抽样调查      B．5.6万学生是总体 C．2000是样本容量              D．2000名考生的数学成绩是总体的一个样本4.如图AB∥CD，AD平分∠BAC，且∠C＝80°，则∠D的度数是（　　）A．60°      B．50°           C．45°            D．40° 5.点P（2﹣a，2a﹣1）在第四象限，且到y轴的距离为3，则a的值为（　　）A．﹣1 B．﹣2 C．1 D．26.内角和等于外角和2倍的多边形是（　　）A．五边形 B．六边形 C．七边形 D．八边形7.如图，将一张三角形纸片的一角折叠，使点落在外的处，折痕为．如果，，，那么下列式子中正确的是　　A． B． C． D． 8.为了了解2018年北京市乘坐地铁的每个人的月均花费情况，相关部门随机调查了1000人乘坐地铁的月均花费（单位：元），绘制了如下频数分布直方图，根据图中信息，下面3个推断中，合理的是　　①小明乘坐地铁的月均花费是75元，那么在所调查的1000人中至少有一半以上的人月均花费超过小明；②估计平均每人乘坐地铁的月均花费的范围是元；③如果规定消费达到一定数额可以享受折扣优惠，并且享受折扣优惠的人数控制在左右，那么乘坐地铁的月均花费达到120元的人可享受折扣．A．①② B．①③ C．②③ D．①②③ 二、填空题（每小题2分，共16分）.9．为了解某市4万名学生平均每天读书的时间，请你运用所学的统计知识， 将统计的主要步骤进行排序：①从4万名学生中随机抽取400名学生，调查他们平均每天读书的时间；②分析数据；③得出结论， 提出建议；④利用统计图表将收集的数据整理和表示.合理的排序是　　． （只填序号）10．在△ABC中，∠A＝80°+∠B+∠C，则∠A＝　   　．11．一个样本含有20个数据：68，69，70，66，68，64，65，65，69，62，67，66，65，67，63，65，64，61，65，66，在列频数分布表时，64.5～66.5这组的频数为 　   　．12．课间操时，小华、小军和小刚的位置如图所示，如果小华的位置用表示，小军的位置用表示，那么小刚的位置可以表示为 　　．13．如图，中，分别是的高和角平分线，若，，则　　．  14.如图，线段，垂足为点，线段分别交、于点，，连结，．则的度数为 　　．  15. 如图，在平面直角坐标系中，直线与轴在正半轴、轴正半轴分别交、两点，点在的延长线上，平分，平分，则的度数是　　．  16.在平面直角坐标系中，对于点，我们把点叫做点的伴随点．知点的伴随点为，点的伴随点为，点的伴随点为，，这样依次得到点，，，，，．若点的坐标为，则点的坐标为　　；若点的坐标为，对于任意的正整数，点均在轴上方，则，应满足的条件为　　． 三、解答题（本题共68分，第17-20题每题5分，第21-23题，每题6分，第24-25题，每题5分，第26题6分，第27-28题，每题7分)解答应写出文字说明、演算步骤或证明过程）.17．已知等腰三角形的周长为18cm，其中两边之差为3cm，求三角形的各边长．   18．如图，AE∥BD，∠1＝115°，∠2＝35°，求∠C的度数．   19.如图，在中，，，的外角的平分线交的延长线于点．（1）补全图形；（2）求的度数；（3）已知为延长线上一点，连接，若，请判断与的位置关系为： 　　．   20．已知点，试分别根据下列条件，求出点的坐标:（1）点在轴上；（2）点在过点，且与轴平行的直线上．   21. 如图，已知△ABC中，∠ABC和∠ACB的平分线BD、CE相交于点O，且∠A＝60°，求∠BOC的度数．                        22．对有序数对定义“运算”： ，，，其中，为常数，运算的结果也是一个有序数对，在此基础上，可对平面直角坐标系中的任意一点规定“变换”；点在的变换下的对应点即为坐标是的点．（1）当，时，　　．（2）若点在变换下的对应点是它本身，求的值．    23．如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．（1）画出三角形ABC，并求其面积；（2）如图，△A′B′C′是由△ABC经过 　   　平移得到的．（3）已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标是（ 　   　，　   　）．   24．如图1所示，在△ABC中，AE是∠BAC的平分线，∠B＜∠C，F为AE上一点，且FD⊥BC于D．（1）试推导∠EFD与∠B、∠C的大小关系．（2）如图2所示，当点F在AE的延长线上时，其余条件不变，在（1）中推导的结论还成立吗？请说明理由．           25.为庆祝中国共产党建党100周年，使学生进一步了解中国共产党的历史，某学校组织了“党史百年天天读”活动，并进行了一次全校2000名学生都参加的书面测试，阅卷后，教学处随机抽取了100份答卷进行分析统计，发现考试成绩（分的最低分为50分，最高分为满分100分，且分数都为整数，并绘制了尚不完整的统计图表：分数段分）频数频率40.040.20300.3026150.1550.05请根据统计图表提供的信息，解答下列问题：（1）在频数分布表中，　　；　　；（2）请将频数分布直方图补充完整，并在图中标明相应数据；（3）该校对成绩为的学生进行奖励，按成绩从高分到低分设一，二，三等奖，各奖项的人数占比如扇形统计图所示．①在扇形图中，二等奖所在扇形的圆心角度数为 　　；②请你估算全校获得一等奖的学生人数约为 　　人．   26.阅读与理解：三角形的中线的性质：三角形的中线等分三角形的面积，即如图1，是中边上的中线，则．理由：，，即：等底同高的三角形面积相等．操作与探索在如图2至图4中，的面积为．（1）如图2，延长的边到点，使，连接．若的面积为，则　　（用含的代数式表示）；（2）如图3，延长的边到点，延长边到点，使，，连接．若的面积为，则　　（用含的代数式表示），并写出理由；     （3）在图3的基础上延长到点，使，连接，，得到（如图．若阴影部分的面积为，则　　（用含的代数式表示）．拓展与应用:如图5，已知四边形的面积是，、、、分别是、、、的中点，连接FH，EG交于点O，求图中阴影部分的面积？     27.在△ABC中，∠ACB=90°，∠ABC=40°，P是射线BC上一动点（与B，C点不重合）．连接AP，过点C作CD⊥AP于点D，交直线AB于点E，设∠APC =．（1）若点P在线段BC上，且60°，如图1，直接写出∠PAB的大小；（2）若点P在线段BC上运动，如图2，求∠AED的大小（用含的式子表示）；（3）若点P在线段BC的延长线上运动，且≠50°，直接写出∠AED 的大小（用含 的式子表示）．           28.在平面直角坐标系中，对于任意两点，，，，定义为点和点的“阶距离”，其中．例如：点，的阶距离”为．已知点．（1）若点，求点和点的“阶距离”；（2）若点在轴上，且点和点的“阶距离”为4，求点的坐标；（3）若点，且点和点的“阶距离”为1，直接写出的取值范围．