
山西省吕梁市汾阳市海洪初级中学校2022-2023学年九年级上学期期中考试数学试题(含答案)
展开
这是一份山西省吕梁市汾阳市海洪初级中学校2022-2023学年九年级上学期期中考试数学试题(含答案),共25页。试卷主要包含了填空题等内容,欢迎下载使用。
九年级(上)期中数学试卷
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题列出的四个选项中,只有一项是最符合题目要求的,请将正确选项的字母标号在答题卡相应位置涂黑。
1.疫情防控期间,无数医护人员坚守在抗疫防疫第一线,下列有关医护的图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.将一元二次方程3x2﹣1=2x化成一般形式后(二次项系数为正数),二次项系数和一次项系数分别是( )
A.3、﹣2 B.3、2 C.3、﹣1 D.3、1
3.若关于x的方程x2﹣5x+2k=0没有实数根,则k的值可能是( )
A.﹣2 B.0 C.2 D.4
4.如图,在正方形网格中,线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点,A的对应点是点C),若点A的坐标为(﹣1,5),点B的坐标为(3,3),则旋转中心O点的坐标为( )
A.(1,1) B.(4,4)
C.(2,1) D.(1,1)或(4,4)
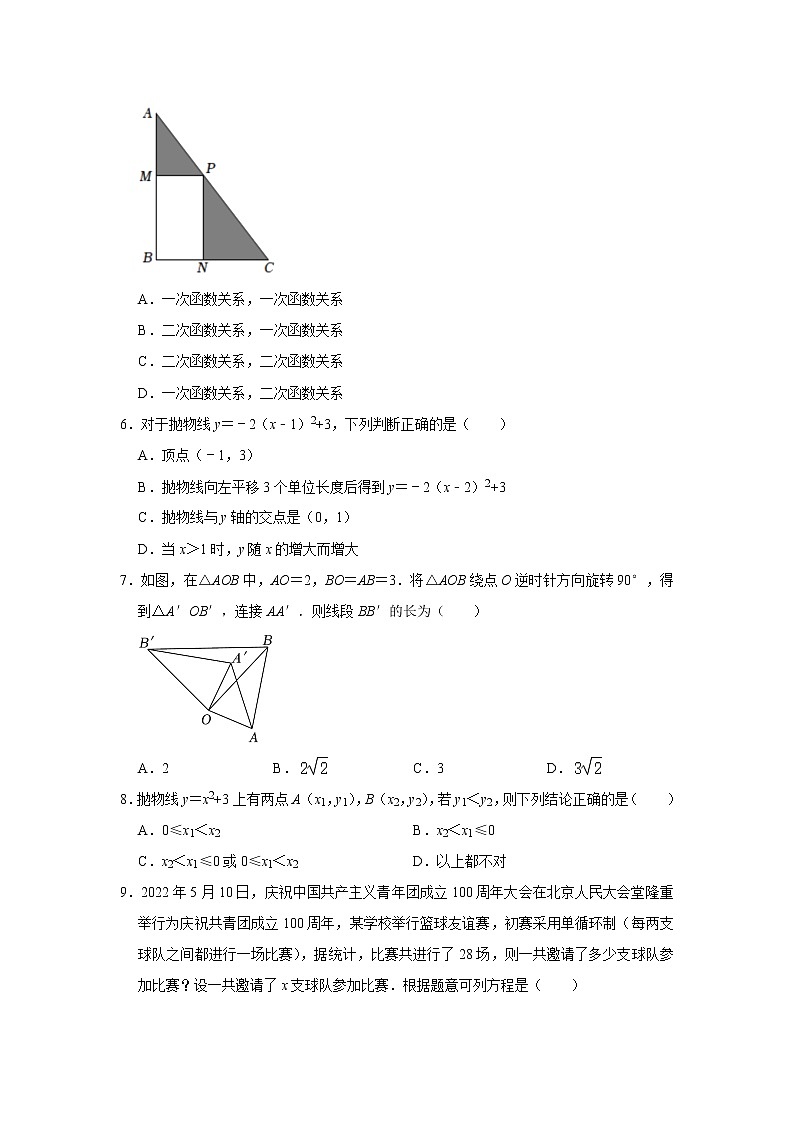
5.如图,某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN,其中点P在AC上点N,M分别在BC,AB上,记PM=x,PN=y,图中阴影部分的面积为S,若NP在一定范围内变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,一次函数关系
B.二次函数关系,一次函数关系
C.二次函数关系,二次函数关系
D.一次函数关系,二次函数关系
6.对于抛物线y=﹣2(x﹣1)2+3,下列判断正确的是( )
A.顶点(﹣1,3)
B.抛物线向左平移3个单位长度后得到y=﹣2(x﹣2)2+3
C.抛物线与y轴的交点是(0,1)
D.当x>1时,y随x的增大而增大
7.如图,在△AOB中,AO=2,BO=AB=3.将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,连接AA′.则线段BB′的长为( )
A.2 B. C.3 D.
8.抛物线y=x2+3上有两点A(x1,y1),B(x2,y2),若y1<y2,则下列结论正确的是( )
A.0≤x1<x2 B.x2<x1≤0
C.x2<x1≤0或0≤x1<x2 D.以上都不对
9.2022年5月10日,庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行为庆祝共青团成立100周年,某学校举行篮球友谊赛,初赛采用单循环制(每两支球队之间都进行一场比赛),据统计,比赛共进行了28场,则一共邀请了多少支球队参加比赛?设一共邀请了x支球队参加比赛.根据题意可列方程是( )
A.=28 B.=28 C.x(x﹣1)=28 D.x(x+1)=28
10.已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( )
A.a﹣b+c>0 B.abc>0 C.4a﹣2b+c<0 D.2a﹣b=0
二、填空题(本大题共5个小题,每小题3分,共15分)
11.在平面直角坐标系中,若点P(m,m﹣n)与点Q(2,1)关于原点对称,则点M(m,n)在第 象限.
12.在平面直角坐标系中,抛物线y=x2﹣2x+2的顶点坐标为 .
13.利用配方法解一元二次方程x2﹣6x+7=0时,将方程配方为(x﹣m)2=n,则mn= .
14.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣3,6),B(1,3),则方程ax2﹣bx﹣c=0的解是 .
15.如图,在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(1,1)、(1,3)、(3,3).若抛物线y=ax2的图象与正方形ABCD有公共点,则a的取值范围是 .
三、解答题(本大题共8个小题,共75分)解答应写出文字说明,正明过程或演算步骤。
16.(8分)用适当的方法解下列方程:
(1)(2x﹣1)2=3x(2x﹣1);
(2)3x2﹣5x+5=7.
17.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣4,2),C(﹣3,4).
(1)请画出△ABC绕着原点O顺时针旋转90°的△A1B1C1;
(2)若△ABC的对应点分别为A1、B1、C1;请写出点A1、B1、C1的坐标,观察对应点之间的坐标特征,若点P(a,b)在△ABC上,写出点P的对应点P1的坐标.
(3)若△A2B2C2与△ABC关于原点O成中心对称,写出点A的对应点A2的坐标.
18.(8分)如图,抛物线y=﹣+与x轴交于A、B两点,与y轴交于C点.
(1)求A、B、C三点的坐标;
(2)证明△ABC为直角三角形.
19.(9分)2022年4月8日,CCTV﹣13新闻频道《朝闻天下》,报道了山东新泰《香椿进入收获期,“椿”意盎然助增收》,我市香椿畅销全国各地.当地某电商对一款成本价为30元的香椿商品进行直播销售,如果按每件40元销售,平均每月可卖出600件.通过市场调查发现,每件香椿商品售价每上涨1元,其月销售量就将减少10件.为了实现平均每月12000元的销售利润,
(1)这种商品的售价应定为多少?
(2)这时商家每月能售出该香椿商品多少件?
20.(9分)问题提出
在学完乘法公式(a±b)2=a2±2ab+b2后,王老师向同学们提出了这样一个问题:你能求代数式﹣x2+2x+3的最大值吗?
初步思考
同学们经过交流、讨论,总结出如下方法:
解:﹣x2+2x+3=﹣(x2﹣2x)+3=﹣(x2﹣2x+1﹣1)+3=﹣(x2﹣2x+1)+1+3=﹣(x2﹣2x+1)+4=﹣(x﹣1)2+4
因为(x﹣1)2≥0,
所以﹣(x﹣1)2≤0.
所以当x=1时,﹣(x﹣1)2的值最大,最大值是0.
所以当﹣(x﹣1)2=0时,﹣(x﹣1)2+4的值最大,最大值是4.
所以﹣x2+2x+3的最大值是4.
尝试应用
(1)求代数式﹣x2+14x+10的最大值,并写出相应的x的值.
拓展提高
(2)将一根长24cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,那么这两个正方形面积之和有最小值吗?若有,求此时这根铁丝剪成两段后的长度及这两个正方形面积的和;若没有,请说明理由.
21.(9分)如图,二次函数y=x2﹣3x+c的图象与x轴的一个交点为A(4,0),另一个交点为B,且与y轴交于点C.
(1)求二次函数的解析式;
(2)求△ABC的面积;
(3)该二次函数图象上是否存在点D,使△ABD与△ABC的面积相等?若存在,请求出D点的坐标;若不存在,请说明理由.
22.(11分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,∠ACD=30°,以D为顶点作∠MDN,交边AC,BC于点M,N,∠MDN=60°,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图1,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,∠ACD=45°,以D为顶点作∠MDN,交边AC,BC于点M,N,∠MDN=∠ADB,连接MN.
(1)先猜想AM,MN,BN三条线段之间的数量关系,再证明.
(2)∠MDN绕点D旋转,当M,N分别在CA,BC的延长线上,完成图2,其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请对慧慧同学所编制的问题进行解答.
23.(13分)第二十四届冬奥会在北京成功举办,我国选手在跳台滑雪项目中夺得金牌.在该项目中,运动员首先沿着跳台助滑道飞速下滑,然后在起跳点腾空,身体在空中飞行至着陆坡着陆,再滑行到停止区终止.本项目主要考核运动员的飞行距离和动作姿态,某数学兴趣小组对该项目中的数学问题进行了深入研究:
如图为该兴趣小组绘制的赛道截面图,以停止区CD所在水平线为x轴,过起跳点A与x轴垂直的直线为y轴,O为坐标原点,建立平面直角坐标系.着陆坡AC的坡角为30°,OA=65m,某运动员在A处起跳腾空后,飞行至着陆坡的B处着陆,AB=100m.在空中飞行过程中,运动员到x轴的距离y(m)与水平方向移动的距离x(m)具备二次函数关系,其解析式为y=﹣x2+bx+c.
(1)求b,c的值;
(2)进一步研究发现,运动员在飞行过程中,其水平方向移动的距离x(m)与飞行时间t(s)具备一次函数关系,当运动员在起跳点腾空时,t=0,x=0;空中飞行5s后着陆.
①求x关于t的函数解析式;
②当t为何值时,运动员离着陆坡的竖直距离h最大,最大值是多少?
九年级(上)期中数学试卷
(参考答案与详解)
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题列出的四个选项中,只有一项是最符合题目要求的,请将正确选项的字母标号在答题卡相应位置涂黑。
1.疫情防控期间,无数医护人员坚守在抗疫防疫第一线,下列有关医护的图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形和轴对称图形的定义进行判断.
【解答】解:A.是轴对称图形,不是中心对称图形,故本选项不合题意;
B.既是轴对称图形又是中心对称图形,,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.不是是轴对称图形,也不是中心对称图形,故本选项不合题意;
故选:B.
2.将一元二次方程3x2﹣1=2x化成一般形式后(二次项系数为正数),二次项系数和一次项系数分别是( )
A.3、﹣2 B.3、2 C.3、﹣1 D.3、1
【分析】先化成一元二次方程的一般形式,再找出二次项系数和一次项系数即可.
【解答】解:∵3x2﹣1=2x,
∴3x2﹣2x﹣1=0,
∴二次项系数和一次项系数分别是3和﹣2,
故选:A.
3.若关于x的方程x2﹣5x+2k=0没有实数根,则k的值可能是( )
A.﹣2 B.0 C.2 D.4
【分析】先根据判别式的意义得到Δ=(﹣5)2﹣4×2k<0,从而得到k的取值范围,然后对各选项进行判断.
【解答】解:根据题意得Δ=(﹣5)2﹣4×2k<0,
解得k>,
所以k可以取4.
故选:D.
4.如图,在正方形网格中,线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点,A的对应点是点C),若点A的坐标为(﹣1,5),点B的坐标为(3,3),则旋转中心O点的坐标为( )
A.(1,1) B.(4,4)
C.(2,1) D.(1,1)或(4,4)
【分析】先按点A、点B的坐标确定坐标原点,画出平面直角坐标系,对应点A与C、B与D连线的垂直平分线的交点即为旋转中心.
【解答】解:作AC、BD的垂直平分线交于点E,
点E即为旋转中心,E(1,1),
故选:A.
5.如图,某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN,其中点P在AC上点N,M分别在BC,AB上,记PM=x,PN=y,图中阴影部分的面积为S,若NP在一定范围内变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,一次函数关系
B.二次函数关系,一次函数关系
C.二次函数关系,二次函数关系
D.一次函数关系,二次函数关系
【分析】设AB=m(m为常数),根据等腰直角三角形的性质得到AM=PM,根据矩形的性质得到PN=BM,得到y=﹣x+m,根据三角形和矩形的面积得到结论.
【解答】解:设AB=m(m为常数),
在△AMP中,∠A=45°,AM⊥PM,
∴△AMP为等腰直角三角形,
∴AM=PM,
∵四边形PMBN是矩形,
∴PN=BM,
∴x+y=PM+PN=AM+BM=AB=m,
即y=﹣x+m,
∴y与x成一次函数关系,
∵S=S△ABC﹣S矩形PMBN=m2﹣xy=m2﹣x(﹣x+m)=x 2﹣mx+m2,
∴S与x成二次函数关系.
故选:D.
6.对于抛物线y=﹣2(x﹣1)2+3,下列判断正确的是( )
A.顶点(﹣1,3)
B.抛物线向左平移3个单位长度后得到y=﹣2(x﹣2)2+3
C.抛物线与y轴的交点是(0,1)
D.当x>1时,y随x的增大而增大
【分析】根据二次函数解析式结合二次函数的性质以及平移的规律,即可得出结论.
【解答】解:A、∵y=﹣2(x﹣1)2+3,
∴抛物线的顶点(1,3),故错误,本选项不符合题意,
B、抛物线向左平移3个单位长度后得到y=﹣2(x﹣1+3)2+3,y=﹣2(x+2)2+3,故错误,即本选项不符合题意,
C、当x=0时,y=1,抛物线与y轴的交点是(0,1),故正确,本选项符合题意,
D、∵y=﹣2(x﹣1)2+3,
∴开口向下,对称轴为直线x=1,
∴当x>1时,y随x的增大而减小,故错误,本选项不符合题意,
故选:C.
7.如图,在△AOB中,AO=2,BO=AB=3.将△AOB绕点O逆时针方向旋转90°,得到△A′OB′,连接AA′.则线段BB′的长为( )
A.2 B. C.3 D.
【分析】由旋转的性质可得BO=B'O=3,∠BOB'=90°,由勾股定理可求解.
【解答】解:∵将△AOB绕点O逆时针方向旋转90°,
∴BO=B'O=3,∠BOB'=90°,
∴BB'===3,
故选:D.
8.抛物线y=x2+3上有两点A(x1,y1),B(x2,y2),若y1<y2,则下列结论正确的是( )
A.0≤x1<x2 B.x2<x1≤0
C.x2<x1≤0或0≤x1<x2 D.以上都不对
【分析】根据二次函数的性质判断即可.
【解答】解:∵抛物线y=x2+3上有两点A(x1,y1),B(x2,y2),且y1<y2,
∴|x1|<|x2|,
∴0≤x1<x2或x2<x1≤0或0<﹣x1<x2或0<x1<﹣x2,
故选:D.
9.2022年5月10日,庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行为庆祝共青团成立100周年,某学校举行篮球友谊赛,初赛采用单循环制(每两支球队之间都进行一场比赛),据统计,比赛共进行了28场,则一共邀请了多少支球队参加比赛?设一共邀请了x支球队参加比赛.根据题意可列方程是( )
A.=28 B.=28 C.x(x﹣1)=28 D.x(x+1)=28
【分析】设一共邀请了x支球队参加比赛,赛制为单循环形式(每两支球队之间都进行一场比赛),则每个队参加(x﹣1)场比赛,则共有场比赛,可以列出一元二次方程.
【解答】解:由题意得,=28.
故选:B.
10.已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( )
A.a﹣b+c>0 B.abc>0 C.4a﹣2b+c<0 D.2a﹣b=0
【分析】根据二次函数图象判断出a,b,c的正负关系,对称轴,顶点坐标等,再进行判断即可.
【解答】解:由图象可知,当x=﹣1时,y=a﹣b+c>1,故A项正确,不符合题意;
∵抛物线开口向下,﹣=﹣1,与y轴的交点为(0,1),
∴a<0,b=2a<0,c=1>0,
∴2a﹣b=0,abc>0,故B、D项正确,不符合题意;
∵抛物线的对称轴为直线x=﹣1,与x轴的一个交点在原点和点(1,0)之间,
∴另一个交点在(﹣2,0)与(﹣3,0)之间,
∴当x=﹣2时,y=4a﹣2b+c>0,故C项错误,符合题意,
故选:C.
二、填空题(本大题共5个小题,每小题3分,共15分)
11.在平面直角坐标系中,若点P(m,m﹣n)与点Q(2,1)关于原点对称,则点M(m,n)在第 三 象限.
【分析】直接利用关于原点对称点的性质得出m,n的值,再利用各象限内点的坐标特点得出答案.
【解答】解:∵点P(m,m﹣n)与点Q(2,1)关于原点对称,
∴,
解得:,
∴点M(m,n)即(﹣2,﹣1)在第三象限.
故答案为:三.
12.在平面直角坐标系中,抛物线y=x2﹣2x+2的顶点坐标为 (1,1) .
【分析】首先配方得出二次函数顶点式进而得出答案.
【解答】解:∵y=x2﹣2x+2=(x﹣1)2+1,
∴抛物线y=x2﹣2x+2的顶点坐标为(1,1).
故答案为:(1,1).
13.利用配方法解一元二次方程x2﹣6x+7=0时,将方程配方为(x﹣m)2=n,则mn= 6 .
【分析】方程移项后,两边加上一次项一半的平方,利用完全平方公式配方得到结果,求出m与n的值,即可求出mn的值.
【解答】解:方程x2﹣6x+7=0,
移项得:x2﹣6x=﹣7,
配方得:x2﹣6x+9=2,即(x﹣3)2=2,
∵方程配方为(x﹣m)2=n,
∴m=3,n=2,
则mn=3×2=6.
故答案为:6.
14.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣3,6),B(1,3),则方程ax2﹣bx﹣c=0的解是 x1=﹣3,x2=1 .
【分析】利用图象法即可解决问题,方程的解就是两个函数图象的交点的横坐标.
【解答】解:由图象可知,关于x的方程ax2﹣bx﹣c=0的解,就是抛物线y=ax2(a≠0)与直线y=bx+c(b≠0)的两个交点坐标分别为A(﹣3,6),B(1,3)的横坐标,
即x1=﹣3,x2=1.
故答案为:x1=﹣3,x2=1.
15.如图,在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(1,1)、(1,3)、(3,3).若抛物线y=ax2的图象与正方形ABCD有公共点,则a的取值范围是 ≤a≤3 .
【分析】求出抛物线经过两个特殊点时的a的值即可解决问题.
【解答】解:∵正方形ABCD的顶点A、B、C的坐标分别为(1,1)、(1,3)、(3,3).
∴D(3,1),
当抛物线经过点B(1,3)时,则a=3,
当抛物线经过D(3,1)时,a=,
观察图象可知≤a≤3,
故答案为:≤a≤3.
三、解答题(本大题共8个小题,共75分)解答应写出文字说明,正明过程或演算步骤。
16.(8分)用适当的方法解下列方程:
(1)(2x﹣1)2=3x(2x﹣1);
(2)3x2﹣5x+5=7.
【分析】(1)根据因式分解法解一元二次方程即可;
(2)根据公式法解一元二次方程即可.
【解答】解:(1)(2x﹣1)2=3x(2x﹣1),
∴(2x﹣1)(2x﹣1﹣3x)=0,
∴2x﹣1=0或﹣x﹣1=0,
解得,x2=﹣1;
(2)3x2﹣5x+5=7,
∴3x2﹣5x﹣2=0,
∵Δ=(﹣5)2﹣4×3×(﹣2)=49>0,
∴x=,
∴x1=2,.
17.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣4,2),C(﹣3,4).
(1)请画出△ABC绕着原点O顺时针旋转90°的△A1B1C1;
(2)若△ABC的对应点分别为A1、B1、C1;请写出点A1、B1、C1的坐标,观察对应点之间的坐标特征,若点P(a,b)在△ABC上,写出点P的对应点P1的坐标.
(3)若△A2B2C2与△ABC关于原点O成中心对称,写出点A的对应点A2的坐标.
【分析】(1)根据旋转的性质即可画出△ABC绕着原点O顺时针旋转90°的△A1B1C1;
(2)根据旋转的性质,结合(1)即可解决问题;
(3)根据△A2B2C2与△ABC关于原点O成中心对称,进而可以写出点A的对应点A2的坐标.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)A1(1,1),B1(2,4),C1(4,3),点P1的坐标(b,﹣a);
(3)点A2的坐标为(1,﹣1).
18.(8分)如图,抛物线y=﹣+与x轴交于A、B两点,与y轴交于C点.
(1)求A、B、C三点的坐标;
(2)证明△ABC为直角三角形.
【分析】(1)令y=0,则﹣+=0,解方程求出x的值即得到点A、B的坐标;令x=0,求出y的值,即得到点C的坐标;
(2)先由点A、B、C的坐标分别求出OA、OB、OC的长,再根据勾股定理分别求出AC2、BC2、AB2,可得AC2+BC2=AB2,即可根据勾股定理的逆定理证明△ABC是直角三角形.
【解答】(1)解:对于抛物线y=﹣+,当y=0时,则﹣+=0,
解得x1=﹣,x2=2;
当x=0时,y=2,
∴A(﹣,0),B(2,0),C(0,2).
(2)证明:连接AC,BC,
∵OA=,OB=2,∠AOC=∠BOC=90°,
∴AC2=()2+22=6,BC2=(2)2+22=12,
∴AC2+BC2=6+12=18;
∵AB=2﹣(﹣)=3,
∴AB2=(3)2=18,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
19.(9分)2022年4月8日,CCTV﹣13新闻频道《朝闻天下》,报道了山东新泰《香椿进入收获期,“椿”意盎然助增收》,我市香椿畅销全国各地.当地某电商对一款成本价为30元的香椿商品进行直播销售,如果按每件40元销售,平均每月可卖出600件.通过市场调查发现,每件香椿商品售价每上涨1元,其月销售量就将减少10件.为了实现平均每月12000元的销售利润,
(1)这种商品的售价应定为多少?
(2)这时商家每月能售出该香椿商品多少件?
【分析】(1)设这种商品的涨价x元,根据题意得方程解方程即可得到结论;
(2)根据题意列式计算即可得到结论.
【解答】解:(1)设这种商品的涨价x元,根据题意得,
(40+x﹣30)(600﹣10x)=12000,
解得,x1=20,x2=30,
40+20=60,40+30=70,
答:这种商品的售价应定为60元或70元;
(2)600﹣20×10=400,600﹣30×10=300,
答:这时商家每月能售出该香椿商品400件或300件.
20.(9分)问题提出
在学完乘法公式(a±b)2=a2±2ab+b2后,王老师向同学们提出了这样一个问题:你能求代数式﹣x2+2x+3的最大值吗?
初步思考
同学们经过交流、讨论,总结出如下方法:
解:﹣x2+2x+3=﹣(x2﹣2x)+3=﹣(x2﹣2x+1﹣1)+3=﹣(x2﹣2x+1)+1+3=﹣(x2﹣2x+1)+4=﹣(x﹣1)2+4
因为(x﹣1)2≥0,
所以﹣(x﹣1)2≤0.
所以当x=1时,﹣(x﹣1)2的值最大,最大值是0.
所以当﹣(x﹣1)2=0时,﹣(x﹣1)2+4的值最大,最大值是4.
所以﹣x2+2x+3的最大值是4.
尝试应用
(1)求代数式﹣x2+14x+10的最大值,并写出相应的x的值.
拓展提高
(2)将一根长24cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,那么这两个正方形面积之和有最小值吗?若有,求此时这根铁丝剪成两段后的长度及这两个正方形面积的和;若没有,请说明理由.
【分析】(1)原式利用完全平方公式配方后,利用非负数的性质求出最大值,以及此时x的值即可;
(2)设一段为x,则另一段为24﹣x,表示出两个正方形的面积之和S,利用完全平方公式配方后,根据非负数的性质求出最小值,以及此时x的值即可.
【解答】解:(1)﹣x2+14x+10
=﹣(x2﹣14x+49)+59
=﹣(x﹣7)2+59,
当x=7时,原式有最大值,最大值为59;
(2)设一段为x,则另一段为24﹣x,
根据题意得:
S=()2+(6﹣)2
=x2﹣3x+36
=(x﹣12)2+18,
当x=12时,S有最小值,最小值为18,
则两个正方形面积之和有最小值,此时这根铁丝剪成两段后的长度12cm,12cm,这两个正方形面积的和为18cm2.
21.(9分)如图,二次函数y=x2﹣3x+c的图象与x轴的一个交点为A(4,0),另一个交点为B,且与y轴交于点C.
(1)求二次函数的解析式;
(2)求△ABC的面积;
(3)该二次函数图象上是否存在点D,使△ABD与△ABC的面积相等?若存在,请求出D点的坐标;若不存在,请说明理由.
【分析】(1)把A点代入=x2﹣3x+c中求出c的值,从而得到抛物线解析式;
(2)先解方程x2﹣3x﹣4=0得到B(﹣1,0),再确定C(0,﹣4),然后利用三角形面积公式计算;
(3)设D(t,t2﹣3t﹣4),根据三角形面积公式得到×5×|t2﹣3t﹣4|=10,然后解方程得到D点坐标.
【解答】解:(1)把A(4,0)代入y=x2﹣3x+c得16﹣12+c=0,
解得c=﹣4,
∴抛物线解析式为y=x2﹣3x﹣4;
(2)当y=0时,x2﹣3x﹣4=0,
解得x1=﹣1,x2=4,
∴B(﹣1,0),
当x=0时,y=x2﹣3x﹣4=﹣4,
∴C(0,﹣4),
∴△ABC的面积=×(4+1)×4=10;
(3)存在.
设D(t,t2﹣3t﹣4),
∵△ABD与△ABC的面积相等,
∴×5×|t2﹣3t﹣4|=10,
即|t2﹣3t﹣4|=4,
解方程t2﹣3t﹣4=4得t1=,t2=,
此时D点坐标为(,4)或(,4);
解方程t2﹣3t﹣4=﹣4得t1=0,t2=3,
此时D点坐标为(3,﹣4);
综上所述,D点坐标为(,4)或(,4)或(3,﹣4).
22.(11分)在练习课上,慧慧同学遇到了这样一道数学题:如图,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,∠ACD=30°,以D为顶点作∠MDN,交边AC,BC于点M,N,∠MDN=60°,连接MN.
探究AM,MN,BN三条线段之间的数量关系.
慧慧分析:可先利用旋转,把其中的两条线段“接起来”,再通过证明两三角形全等,从而探究出AM,MN,BN三条线段之间的数量关系.
慧慧编题:在编题演练环节,慧慧编题如下:
如图1,把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,∠ACD=45°,以D为顶点作∠MDN,交边AC,BC于点M,N,∠MDN=∠ADB,连接MN.
(1)先猜想AM,MN,BN三条线段之间的数量关系,再证明.
(2)∠MDN绕点D旋转,当M,N分别在CA,BC的延长线上,完成图2,其余条件不变,直接写出AM,MN,BN三条线段之间的数量关系.
请对慧慧同学所编制的问题进行解答.
【分析】(1)先证四边形ACBD是正方形,可得∠ADM+∠BDN=45°=∠MDN,由旋转的性质可得∠B=∠DAE=90°,AE=BN,DN=DE,∠BDN=∠ADE,由“SAS”可证△MDE≌△MDN,可得MN=ME,可得结论;
(2)方法同(1),由“SAS”可证△MDE≌△MDN,可得MN=ME,可得结论;
【解答】解:(1)MN=AM+BN,理由如下:
∵把两个全等的直角三角板的斜边重合,组成一个四边形ACBD,∠ACD=45°,
∴∠A=∠B=90°,∠ACD=∠BCD=45°,AC=BC,AD=BD,
∴∠A=∠B=∠ACB=90°,
∴四边形ACBD是矩形,
∵AC=BC,
∴四边形ACBD是正方形,
∴∠ADB=90°,
∵∠MDN=∠ADB,
∴∠MDN=45°,
∴∠ADM+∠BDN=45°=∠MDN,
如图,将△BDN绕点D逆时针旋转90°得到△ADE,
∴∠B=∠DAE=90°,AE=BN,DN=DE,∠BDN=∠ADE,
∴∠DAE+∠DAC=180°,∠MDE=∠ADM+∠ADE=∠ADM+∠BDN=∠MDN=45°,
∴点E,点A,点M三点共线,
在△MDE和△MDN中,
,
∴△MDE≌△MDN(SAS),
∴MN=ME,
∴MN=ME=AE+AM=AM+BN;
(2)如图,将△BDN绕点D逆时针旋转90°得到△ADE,
同理可证△MDE≌△MDN(SAS),
∴MN=ME,
∴BN﹣AM=MN.
23.(13分)第二十四届冬奥会在北京成功举办,我国选手在跳台滑雪项目中夺得金牌.在该项目中,运动员首先沿着跳台助滑道飞速下滑,然后在起跳点腾空,身体在空中飞行至着陆坡着陆,再滑行到停止区终止.本项目主要考核运动员的飞行距离和动作姿态,某数学兴趣小组对该项目中的数学问题进行了深入研究:
如图为该兴趣小组绘制的赛道截面图,以停止区CD所在水平线为x轴,过起跳点A与x轴垂直的直线为y轴,O为坐标原点,建立平面直角坐标系.着陆坡AC的坡角为30°,OA=65m,某运动员在A处起跳腾空后,飞行至着陆坡的B处着陆,AB=100m.在空中飞行过程中,运动员到x轴的距离y(m)与水平方向移动的距离x(m)具备二次函数关系,其解析式为y=﹣x2+bx+c.
(1)求b,c的值;
(2)进一步研究发现,运动员在飞行过程中,其水平方向移动的距离x(m)与飞行时间t(s)具备一次函数关系,当运动员在起跳点腾空时,t=0,x=0;空中飞行5s后着陆.
①求x关于t的函数解析式;
②当t为何值时,运动员离着陆坡的竖直距离h最大,最大值是多少?
【分析】(1)根据题意,可以求得点A和点B的坐标,然后代入二次函数解析式,即可得到b、c的值;
(2)①根据题意,可以得到x关于t的函数图象经过的两个点,然后根据待定系数法,即可得到x关于t的函数的解析式;
②先求出直线AB的解析式,再根据题意,可以表示出h,然后根据二次函数的性质,可以求得当h为何值时,运动员离着陆坡的竖直距离h最大,并求出这个最大值.
【解答】解:(1)作BE⊥y轴于点E,
∵OA=65m,着陆坡AC的坡角为30°,AB=100m,
∴点A的坐标为(0,65),AE=50m,BE=50m,
∴OE=OA﹣AE=65﹣50=15(m),
∴点B的坐标为(50,15),
∵点A(0,65),点B(50,15)在二次函数y=﹣x2+bx+c的图象上,
∴,
解得,
即b的值是,c的值是65;
(2)①设x关于t的函数解析式是x=kt+m,
因为点(0,0),(5,50)在该函数图象上,
∴,
解得,
即x关于t的函数解析式是x=10t;
②设直线AB的解析式为y=px+q,
∵点A(0,65),点B(50,15)在该直线上,
∴,
解得,
即直线AB的解析式为y=﹣x+65,
则h=(﹣x2+x+65)﹣(﹣x+65)=﹣x2+x,
∴当x=﹣=25时,h取得最值,此时h=,
∵25<50,
∴x=25时,h取得最值,符合题意,
将x=25代入x=10t,得:25=10t,
解得t=2.5,
即当t为2.5时,运动员离着陆坡的竖直距离h最大,最大值是m.
相关试卷
这是一份山西省吕梁市汾阳市2023-2024学年八年级上学期1月期末数学试题,共7页。
这是一份山西省吕梁市汾阳市2023-2024学年八年级上学期1月期末数学试题,共7页。
这是一份2021-2022学年山西省吕梁市汾阳市海洪中学九年级(上)期末数学试卷(含答案解析),共24页。试卷主要包含了【答案】D,【答案】A,【答案】B,【答案】C等内容,欢迎下载使用。









