上海市闵行区2022-2023学年九年级上期中学期数学试卷 （含答案）

这是一份上海市闵行区2022-2023学年九年级上期中学期数学试卷 （含答案），共20页。试卷主要包含了0分，0分），0分)，【答案】A，【答案】B，【答案】12，【答案】5e等内容，欢迎下载使用。
2022-2023学年上海市闵行区九年级（上）期中数学试卷副标题考试范围：xxx；考试时间：100分钟；命题人：xxx题号一二三总分得分    注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。  第I卷（选择题） 一、选择题（本大题共6小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）下列各组图形中一定是相似形的是(    )A. 两个长方形 B. 两个菱形 C. 两个正方形 D. 两个平行四边形已知中，、分别是边、上的点，下列各式中，不能判断的是(    )A.  B.  C.  D. 如果两个相似三角形对应边的比为：，那么它们的周长比是(    )A. ： B. ： C. ： D. ：若是锐角，，那么锐角等于(    )A.  B.  C.  D. 已知，下列说法中不正确的是(    )A.  B. 与方向相同
C.  D. 如图，一艘船从处向北偏东的方向行驶千米到处，再从处向正西方向行驶千米到处，这时这艘船与的距离(    )
A. 千米 B. 千米 C. 千米 D. 千米第II卷（非选择题） 二、填空题（本大题共12小题，共48.0分）如果：：，那么______．设点是线段的黄金分割点，厘米，那么线段的长是______厘米．已知与单位向量的方向相同，且长度为，那么用表示______．已知在中，，，，那么的值是______．如图，、是边、上的两点，且，：：，那么：______．
已知∽，顶点、、分别与顶点、、对应，、分别是、边上的中线，如果，，，那么的长是______．如图，在平面直角坐标系内有一点，那么与轴正半轴的夹角的余切值______．
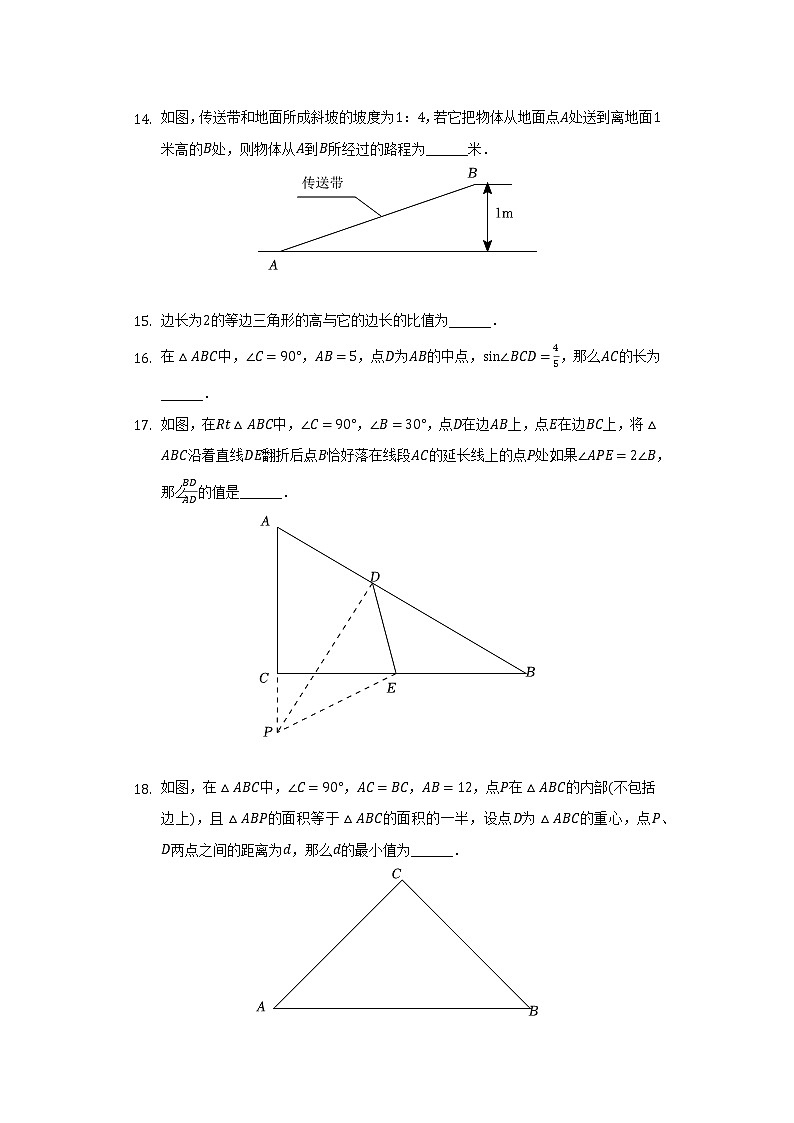
 如图，传送带和地面所成斜坡的坡度为：，若它把物体从地面点处送到离地面米高的处，则物体从到所经过的路程为______米．
边长为的等边三角形的高与它的边长的比值为______．在中，，，点为的中点，，那么的长为______．如图，在中，，，点在边上，点在边上，将沿着直线翻折后，点恰好落在线段的延长线上的点处，如果，那么的值是______．
如图，在中，，，，点在的内部不包括边上，且的面积等于的面积的一半，设点为的重心，点、两点之间的距离为，那么的最小值为______．
  三、解答题（本大题共7小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）本小题分
计算：．本小题分
如图，已知两个不平行的向量、先化简，再求作：．
不要求写作法，但要指出图中表示结论的向量
本小题分
如图，已知在正方形中，，点为边延长线上一点，，联结，线段交于点．
求的值；
求的值．
本小题分
如图，在电线杆上的处引拉线和固定电线杆．在离电线杆米的处安置测角仪点、、在同一直线上，在点处测得电线杆上处的仰角为已知测角仪的高为米，拉线的长为米，求测角仪底端点与拉线固定点之间的距离．
 本小题分
已知：如图，在中，，点、分别在边上，．
求证：；
如果点在边上，且，，求证：∽．
本小题分
已知在平面直角坐标系中如图，直线，与轴、轴分别交于、两点，且点的坐标为，联结，与轴交于点．
求线段的长度；
求点的坐标；
联结，求证：．
本小题分
已知，在中，，，，点、分别在边、上，且均不与顶点重合，如图所示，设，．
当点与点重合时如图所示，求线段的长；
在图中当点不与点重合时，求关于的函数解析式及其定义域；
我们把有一组相邻内角相等的凸四边形叫做等邻角四边形．请阅读理解以上定义，完成问题探究：如图，设点在边上，，如果四边形是等邻角四边形，求线段的长．

答案和解析 1.【答案】 【解析】解：两个正方形的对应角相等，对应边的比相等，
两个正方形一定是相似形，
又两个菱形的对应角不一定相等，两个矩形的边不一定对应成比例，两个平行四边形的对应边不一定对应成比例、对应角不一定相等，
两个菱形、两个矩形、两个平行四边形都不一定是相似形，
故选：．
如果两个多边形的对应角相等，对应边成比例，则这两个多边形是相似多边形．
本题主要考查了相似多边形的性质，相似多边形的性质为：对应角相等；对应边的比相等．
 2.【答案】 【解析】解：如图：

若使线段，则其对应边必成比例，
即，，故选项B、D正确；
，即，故选项C正确；
故A选项答案错误．
故选：．
若使线段，则其对应边必成比例，进而依据对应边成比例即可判定．
本题主要考查了由平行线分线段成比例判定线段平行的问题，能够掌握其性质，并能够通过其性质判定两直线平行．
 3.【答案】 【解析】解：两个相似三角形对应边的比为：，
它们的周长比是：．
故选B．
直接利用相似三角形的性质得出答案．
本题主要考查相似三角形的性质，正确掌握相关性质是解题关键．
 4.【答案】 【解析】解：，
，
，
故选：．
根据特殊锐角三角函数值先得出，再求出即可．
本题考查特殊锐角三角函数值，掌握特殊锐角三角函数值是正确解答的前提．
 5.【答案】 【解析】解：、由知：，原说法不正确，符合题意；
B、由知：与的方向相同，原说法正确，不符合题意；
C、由知：与的方向相同，则，原说法正确，不符合题意；
D、由知：，原说法正确，不符合题意．
故选：．
根据已知条件可知：与的方向相同，其模是倍关系．
本题主要考查了平面向量，注意：平面向量既有方向，又有大小．
 6.【答案】 【解析】解：如图：

，
，
，千米，
千米，千米，
千米，
千米，
故选：．
根据直角三角形的三角函数得出，，进而得出，利用勾股定理得出即可．
此题考查了方向角、解直角三角形的应用，解题的关键是根据直角三角形的三角函数得出，解答．
 7.【答案】 【解析】解：因为：：，
所以，
所以．
故答案为：．
根据：：可得，代入计算即可．
本题考查了比例的性质，掌握比例的性质：内项之积等于外项之积是解题的关键．
 8.【答案】 【解析】解：点是线段的黄金分割点，厘米，
，
厘米，
故答案为：．
根据黄金比值为计算即可．
本题考查的是黄金分割，掌握黄金比值是解题的关键．
 9.【答案】 【解析】解：与单位向量的方向相同，长度为，
．
故答案为：．
根据平行向量的性质求解即可．
本题考查平面向量，解题的关键是理解题意，灵活运用所学知识解决问题．
 10.【答案】 【解析】解：在中，，，，
．
故答案为：．
根据余弦的定义即可求解．
本题主要考查了余弦函数的定义，正确记忆定义是解题的关键．
 11.【答案】 【解析】解：，
∽，
，
故答案为：．
通过证明∽，可求解．
本题考查了相似三角形的判定和性质，证明三角形相似是解题的关键．
 12.【答案】 【解析】解：∽，和是它们的对应中线，，，，
：：，
：：，
的长是，
故答案为：．
利用“相似三角形的周长比等于对应的中线的比”求解即可．
本题考查相似三角形的性质，解题的关键是记住相似三角形的性质，灵活运用所学知识解决问题．
 13.【答案】 【解析】解：过点作轴于点，如图：

由于点，
，，
．
故答案为：．
过点作轴于点，由点的坐标得、的长，根据余切函数的定义得结论．
本题考查了点在平面直角坐标系里的意义及解直角三角形．解决本题的关键是构造直角三角形．
 14.【答案】 【解析】解：过作地面于，如图所示：

：：，
即：：，
米，
米，
即物体从到所经过的路程为米，
故答案为：．
过作地面于，先根据坡比求出的长，再根据勾股定理求出的长即可．
本题考查了解直角三角形的应用坡度坡角问题，熟练掌握坡度的定义，根据题意求出的长是解题的关键．
 15.【答案】 【解析】解：等边三角形的边长是，根据等腰三角形的三线合一，得底边上的高也是底边上的中线，
底边的一半是．
根据勾股定理，得底边上的高是．
所以高与边长的比的比值是，
故答案为：．
根据等边三角形的性质即可得出．
此题考查了比例线段以及等边三角形的性质，熟悉掌握等边三角形的性质以及灵活运用勾股定理．
 16.【答案】 【解析】解：连接，过点作垂直于点，如图：

，点为的中点，
，
，，
，，
，
，
，
，
是的中位线，
．
故答案为：．
连接，过点作于点，根据正弦的定义求出，根据三角形中位线定理求出即可．
本题主要考查了锐角三角函数、直角三角形斜边上的中线等知识，正确记忆相关定义和定理是解题的关键．
 17.【答案】 【解析】解：在中，，
，
，
，
由翻折可知：，，
，
，
，
．
故答案为：．
根据直角三角形的性质可得，由翻折可知：，，然后利用含度角的直角三角形即可解决问题．
本题考查了翻折变换，含度角的直角三角形，解决本题的关键是掌握翻折的性质．
 18.【答案】 【解析】解：过作于点，设、的中点分别为、，连接、，与交于点，则与的交点便是的重心点，如下图，

，，，
，
点为的重心，
，
、分别是、的中点，
，
，
点在的内部不包括边上，且的面积等于的面积的一半，
点在线段上不与、重合，
当与重合时，、之间的距离为最小，其值为，
故答案为：．
过作于点，设、的中点分别为、，连接、，与交于点，则与的交点便是的重心点，点在线段上不与、重合当与重合时，、两点距离最短为，求得的值便可．
本题主要考查了等腰直角三角形的性质，三角形的重心性质，三角形的中位线定理，三角形的面积，关键在于确定点、两点的距离的最小值为．
 19.【答案】解：



． 【解析】把特殊角的三角函数值代入进行计算，即可解答．
本题考查了实数的运算，特殊角的三角函数值，熟练掌握特殊角的三角函数值是解题的关键．
 20.【答案】解：．
如图，即为所求．
 【解析】去括号合并同类向量，再利用三角形法则画出图形即可．
本题考查平面向量，三角形法则，解题的关键是掌握平面向量的加减混合运算，属于中考常考题型．
 21.【答案】解：四边形是正方形，
，，
∽，
，
；
，
∽，
，
，
∽，
，
，
． 【解析】通过证明∽，可求解；
通过证明∽，可求，即可求解．
本题考查了相似三角形的判定和性质，正方形的性质，证明三角形相似是解题的关键．
 22.【答案】解：如图：

过作垂直于，垂足为点，
则米，米，，
，
，
米，

米，
米，
利用勾股定理得米，
米．
答：测角仪底端点与拉线固定点之间的距离是米． 【解析】过作垂直于，垂足为，根据正切的定义求出，得到的长，根据勾股定理计算即可．
本题考查的是解直角三角形的应用仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．
 23.【答案】证明：，
，
，
，
∽，
，
，
；
如图，

，
∽，
，
又，
，
，
，
，
又，
，
∽． 【解析】通过证明∽，可得，可得结论；
通过证明∽，可证，由等腰三角形的性质和平行线的性质可得，可得结论．
本题考查了相似三角形的判定和性质，等腰三角形的性质，证明三角形相似是解题的关键．
 24.【答案】解：令，则，
，
，
令，则，
，
，
；
解：设直线的解析式为，
，
解得，
，
令，则，
；
证明：，，
轴，，
，
，
，
，，
，
． 【解析】分别求出、点坐标，再求的长即可；
用待定系数法求出直线的解析式，直线与轴的交点即为点；
根据、点的坐标特点，可判断轴，再分别求出与，即可证明．
本题考查一次函数的图象及性质，熟练掌握一次函数的图象及性质，平面中点的坐标特点，直角三角形三角函数值的求法是解题的关键．
 25.【答案】解：过点作于，

在中，，，，
，
，
，
，
，
，
，
；
过点作于，

，
，
∽，
，
，
，，
，，
∽，
，
，
，
，
，
；
：当时，如图，

，
，
，，，
，
，
当时，

，，
，
，
，
，
，
；
当时，即点与点重合，
由得，
，
；
综上所述，如果四边形是等邻角四边形，线段的长为或或． 【解析】过点作于，利用勾股定理求出，利用面积法可得，利用等角对等边得，根据勾股定理求出，再由等腰三角形的性质得，即可求解；
过点作于，证明∽，∽，根据相似三角形的性质求出、，，即可求解；
分三种情况：当时，当时，当时，分别求解即可．
本题是四边形综合题，考查了相似三角形的判定与性质，直角三角形的性质，勾股定理，等邻角四边形等知识，解题的关键是掌握相似三角形的判定与性质，理解等邻角四边形的定义，要注意数形结合以及分类思想的应用．