
重庆市綦江区古南中学2021-2022学年九年级上学期期中数学试卷 (含答案)
展开重庆市綦江区古南中学2021-2022学年九年级上学期期中数学试卷(解析版)
一.选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.
1.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )
A.戴口罩讲卫生 B.勤洗手勤通风
C.有症状早就医 D.少出门少聚集
2.下列方程是关于x的一元二次方程的是( )
A.x2﹣3x= B.x(x+2)=x2 C.x2=3(x﹣2) D.ax2+bx+c=0
3.如图,点A、B、C在⊙O上,若∠AOB的度数为80°,则∠ACB的度数是( )
A.80° B.40° C.160° D.20°
4.将二次函数y=2x2+2的图象先向左平移3个单位长度,再向下平移1个单位长度后所得新函数图象的表达式为( )
A.y=2(x﹣1)2+3 B.y=﹣2(x+3)2+1
C.y=2(x﹣3)2﹣1 D.y=2(x+3)2+1
5.某型号的手机连续两次降价,每个售价由原来的1188元降到了680元,设平均每次降价的百分率为x,列出方程正确的是( )
A.680(1+x)2=1188 B.1188(1+x)2=680
C.680(1﹣x)2=1188 D.1188(1﹣x)2=680
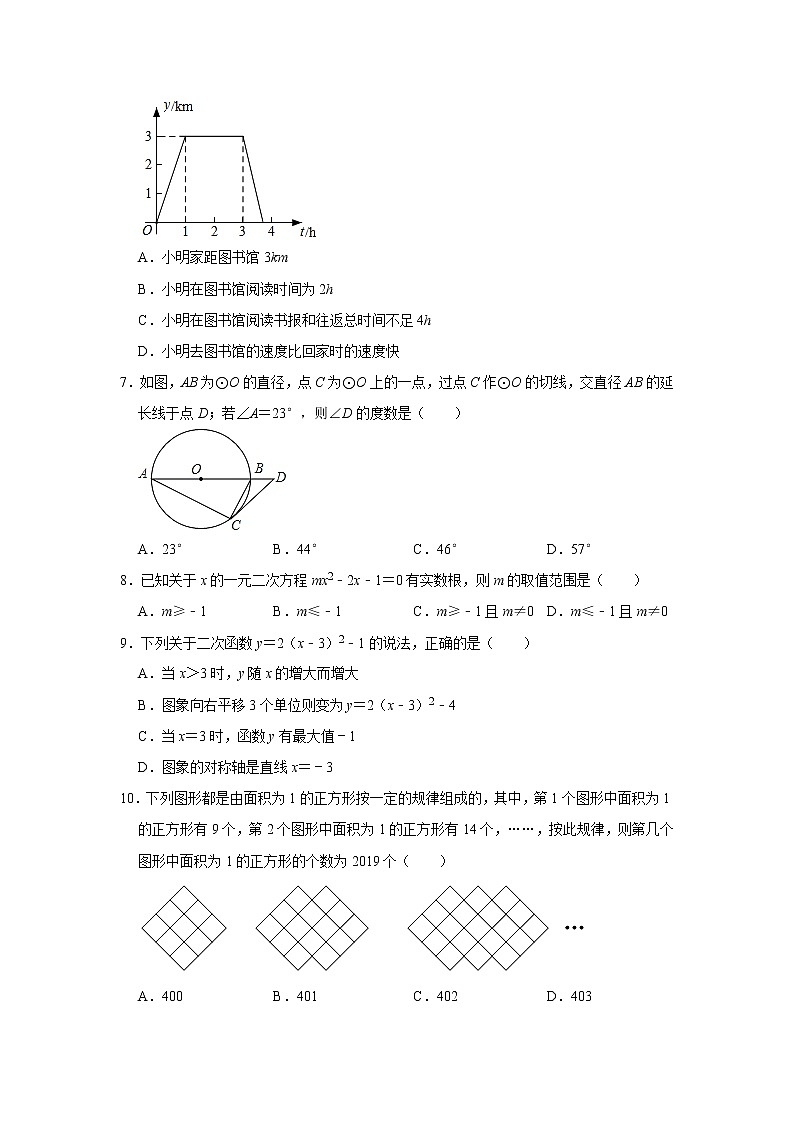
6.小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离y(单位:km)与时间t(单位:h)之间的对应关系.下列描述错误的是( )
A.小明家距图书馆3km
B.小明在图书馆阅读时间为2h
C.小明在图书馆阅读书报和往返总时间不足4h
D.小明去图书馆的速度比回家时的速度快
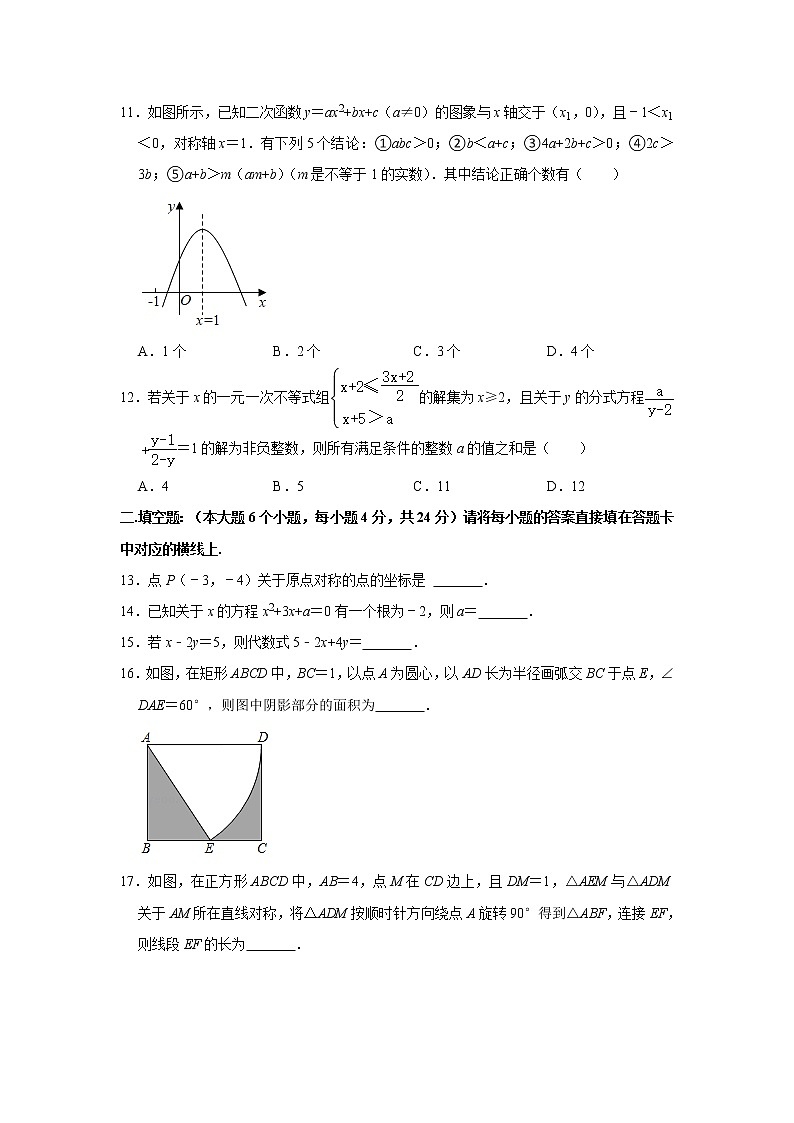
7.如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D;若∠A=23°,则∠D的度数是( )
A.23° B.44° C.46° D.57°
8.已知关于x的一元二次方程mx2﹣2x﹣1=0有实数根,则m的取值范围是( )
A.m≥﹣1 B.m≤﹣1 C.m≥﹣1且m≠0 D.m≤﹣1且m≠0
9.下列关于二次函数y=2(x﹣3)2﹣1的说法,正确的是( )
A.当x>3时,y随x的增大而增大
B.图象向右平移3个单位则变为y=2(x﹣3)2﹣4
C.当x=3时,函数y有最大值﹣1
D.图象的对称轴是直线x=﹣3
10.下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( )
A.400 B.401 C.402 D.403
11.如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(x1,0),且﹣1<x1<0,对称轴x=1.有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c>3b;⑤a+b>m(am+b)(m是不等于1的实数).其中结论正确个数有( )
A.1个 B.2个 C.3个 D.4个
12.若关于x的一元一次不等式组的解集为x≥2,且关于y的分式方程=1的解为非负整数,则所有满足条件的整数a的值之和是( )
A.4 B.5 C.11 D.12
二.填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.
13.点P(﹣3,﹣4)关于原点对称的点的坐标是 .
14.已知关于x的方程x2+3x+a=0有一个根为﹣2,则a= .
15.若x﹣2y=5,则代数式5﹣2x+4y= .
16.如图,在矩形ABCD中,BC=1,以点A为圆心,以AD长为半径画弧交BC于点E,∠DAE=60°,则图中阴影部分的面积为 .
17.如图,在正方形ABCD中,AB=4,点M在CD边上,且DM=1,△AEM与△ADM关于AM所在直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为 .
18.为了践行“金山银山,不如绿水青山”的环保理念.重外环保小组的孩子们参与社区公益活动﹣收集废旧电池.活动开展一个月后,经过统计发现,全组成员平均每人收集了36颗废旧电池.其中,收集数量低于30颗的同学平均每人收集了28颗,收集数量不低于30颗的同学平均每人收集了42颗.数学王老师发现,若每人再多收集5颗,则收集数量低于30颗的同学平均每人收集了29颗,收集数量不低于30颗的同学平均每人收集了45颗并且该环保小组的人数介于40至60人.则该环保小组有 人.
三.解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
19.(10分)(1)解方程:2x2﹣3x+1=0;
(2)化简:÷(+m﹣1).
20.(10分)如图,在直角坐标系中,点A,B,C的坐标分别为(3,3),(4,0),(0,2),将△ABC绕着点C顺时针旋转90°得△A1B1C,其中点A的对应点为点A1.
(1)请画出旋转后的△A1B1C,并写出A1的坐标;
(2)求出在旋转过程中点A所走过的路径长.(结果保留π)
21.(10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连接AC,若CA=CP,∠A=30°.
(1)求证:CP是⊙O的切线;
(2)若OA=1,求弦AC的长.
22.(10分)借鉴我们已有研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象与性质,研究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣2
﹣1
0
1
2
3
4
5
…
y
…
10
m
﹣2
1
n
1
﹣2
3
10
…
其中,m= ,n= ;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①写出函数的一条图象性质: ;
②当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出b的取值范围为 .
23.(10分)为了创建国家级卫生城区,某社区在九月份购买了甲、乙两种绿色植物共1100盆,共花费了27000元.已知甲种绿色植物每盆20元,乙种绿色植物每盆30元.
(1)该社区九月份购买甲、乙两种绿色植物各多少盆?
(2)十月份,该社区决定再次购买甲、乙两种绿色植物.已知十月份甲种绿色植物每盆的价格比九月份的价格优惠元(a>0),十月份乙种绿色植物每盆的价格比九月份的价格优惠a%.因创卫需要,该社区十月份购买甲种绿色植物的数量比九月份的数量增加了a%,十月份购买乙种绿色植物的数量比九月份的数量增加a%.若该社区十月份的总花费与九月份的总花费恰好相同,求a的值.
24.(10分)若在一个三位自然数中,十位上的数字恰好等于百位与个位上的数字之和,则称这个三位数为“奇异数”.例如,在自然数132中,3=1+2,则132是“奇异数”;在自然数462中,6=4+2,则462是“奇异数”.
(1)请你写出最大的“奇异数”,并证明:任意一个“奇异数”一定能被11整除.
(2)若有“奇异数”能同时被3和7整除,求出这样的“奇异数”.
25.(10分)综合与探究
在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交点C.
(1)求抛物线与直线AC的函数解析式;
(2)若点P是直线AC上方抛物线上的一动点,过点P作PF⊥x轴于点F,交直线AC于点D,求线段PD的最大值.
(3)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.(8分)如图,在边长为6的等边△ABC中,点E为边BC上任意一点,连接AE将线段AE绕点A逆时针旋转60°,点E的对应点是点D,连接ED、CD.
(1)如图1,求证:EC+CD=AB;
(2)如图2,在旋转过程中,取AE、CD的中点F、G,连接FG和FC,当AE⊥BC时,试猜想FG与FC的大小关系,写出你猜想的关系式,并证明;
(3)如图2,在整个旋转过程中,FG的长度是否发生变化,若不变化,直接写出FG的值,若变化,请直接写出FG的取值范围.
参考答案与试题解析
一.选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.
1.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )
A.戴口罩讲卫生 B.勤洗手勤通风
C.有症状早就医 D.少出门少聚集
【分析】直接利用轴对称图形和中心对称图形的概念求解.
【解答】解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C、既是中心对称图形也是轴对称图形,故此选项符合题意;
D、不是轴对称图形,也不是中心对称图形,故此选项不合题意;
故选:C.
【点评】本题考查中心对称图形和轴对称图形的知识,关键是掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.
2.下列方程是关于x的一元二次方程的是( )
A.x2﹣3x= B.x(x+2)=x2 C.x2=3(x﹣2) D.ax2+bx+c=0
【分析】利用一元二次方程定义进行解答即可.
【解答】解:A、含有分式,不是一元二次方程,故此选项不符合题意;
B、由已知方程化简得到:2x=0,未知数的最高次数为1次,不是一元二次方程,故此选项不符合题意;
C、是一元二次方程,故此选项符合题意;
D、当a=0时,它不是一元二次方程,故此选项不符合题意;
故选:C.
【点评】此题主要考查了一元二次方程定义,关键是掌握判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.
3.如图,点A、B、C在⊙O上,若∠AOB的度数为80°,则∠ACB的度数是( )
A.80° B.40° C.160° D.20°
【分析】直接根据圆周角定理求解.
【解答】解:∵∠AOB的度数为80°,
∴∠ACB=∠AOB=40°.
故选:B.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
4.将二次函数y=2x2+2的图象先向左平移3个单位长度,再向下平移1个单位长度后所得新函数图象的表达式为( )
A.y=2(x﹣1)2+3 B.y=﹣2(x+3)2+1
C.y=2(x﹣3)2﹣1 D.y=2(x+3)2+1
【分析】直接根据“上加下减,左加右减”的原则进行解答即可.
【解答】解:由“上加下减,左加右减”的原则可知,将二次函数y=2x2+2的图象先向左平移3个单位长度,再向下平移1个单位长度后所得新函数图象的表达式为y=2(x+3)2+2﹣1,即y=2(x+3)2+1.
故选:D.
【点评】本题考查的是二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
5.某型号的手机连续两次降价,每个售价由原来的1188元降到了680元,设平均每次降价的百分率为x,列出方程正确的是( )
A.680(1+x)2=1188 B.1188(1+x)2=680
C.680(1﹣x)2=1188 D.1188(1﹣x)2=680
【分析】根据降价后的价格=原价(1﹣降低的百分率),本题可先用x表示第一次降价后商品的售价,再根据题意表示第二次降价后的售价,即可列出方程.
【解答】解:设平均每次降价的百分率为x,
由题意得出方程为:1188(1﹣x)2=680.
故选:D.
【点评】本题考查由实际问题抽象出一元二次方程,解决此类两次变化问题,可利用公式a(1﹣x)2=c,其中a是变化前的原始量,c是两次变化后的量,x表示平均每次的降低率.
6.小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离y(单位:km)与时间t(单位:h)之间的对应关系.下列描述错误的是( )
A.小明家距图书馆3km
B.小明在图书馆阅读时间为2h
C.小明在图书馆阅读书报和往返总时间不足4h
D.小明去图书馆的速度比回家时的速度快
【分析】根据题意和函数图象中的数据可以判断各个选项的说法是否正确.
【解答】解:由图象知:
A.小明家距图书馆3km,描述正确,故此选项不符合题意;
B.小明在图书馆阅读时间为3﹣1=2小时,描述正确,故此选项不符合题意;
C.小明在图书馆阅读书报和往返总时间不足4h,描述正确,故此选项不符合题意;
D.因为小明去图书馆需要1小时,回来不足1小时,所以小明去图书馆的速度比回家时的速度慢,描述错误,故此选项符合题意.
故选:D.
【点评】本题考查函数的图象,解答本题的关键是明确题意,利用图象来解答.
7.如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D;若∠A=23°,则∠D的度数是( )
A.23° B.44° C.46° D.57°
【分析】连接OC,如图,利用切线的性质得∠OCD=90°,再根据圆周角定理得到∠COD=2∠A=46°,然后利用互余计算∠D的度数.
【解答】解:连接OC,如图,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠COD=2∠A=46°,
∴∠D=90°﹣46°=44°.
故选:B.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理.
8.已知关于x的一元二次方程mx2﹣2x﹣1=0有实数根,则m的取值范围是( )
A.m≥﹣1 B.m≤﹣1 C.m≥﹣1且m≠0 D.m≤﹣1且m≠0
【分析】根据二次项系数非零结合根的判别式△≥0即可得出关于m的一元一次不等式组,解之即可得出结论.
【解答】解:∵关于x的一元二次方程mx2﹣2x﹣1=0有实数根,
∴,
解得:m≥﹣1且m≠0.
故选:C.
【点评】本题考查了根的判别式以及一元二次方程的定义,根据二次项系数非零结合根的判别式△≥0列出关于m的一元一次不等式组是解题的关键.
9.下列关于二次函数y=2(x﹣3)2﹣1的说法,正确的是( )
A.当x>3时,y随x的增大而增大
B.图象向右平移3个单位则变为y=2(x﹣3)2﹣4
C.当x=3时,函数y有最大值﹣1
D.图象的对称轴是直线x=﹣3
【分析】根据二次函数的性质和平移的规律对各选项分析判断后利用排除法求解.
【解答】解:由二次函数y=2(x﹣3)2﹣1可知:开口向上,对称轴为x=3,当x=3时有最小值是﹣1;当x>3时,y随x的增大而增大,
把二次函数y=2(x﹣3)2﹣1的图象向右平移3个单位得到函数为y=2(x﹣3﹣3)2﹣1,即y=2(x﹣6)2﹣1,
故B、C、D错误,A正确,
故选:A.
【点评】本题考查了二次函数的性质以及二次函数的图象与几何变换,主要利用了开口方向,顶点坐标,对称轴以及二次函数的增减性.
10.下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( )
A.400 B.401 C.402 D.403
【分析】由第1个图形有9个面积为1的小正方形,第2个图形有9+5=14个面积为1的小正方形,第3个图形有9+5×2=19个面积为1的小正方形,…由此得出第n个图形有9+5×(n﹣1)=5n+4个面积为1的小正方形,由此求得答案即可.
【解答】解:第1个图形面积为1的小正方形有9个,
第2个图形面积为1的小正方形有9+5=14个,
第3个图形面积为1的小正方形有9+5×2=19个,
…
第n个图形面积为1的小正方形有9+5×(n﹣1)=5n+4个,
根据题意得:5n+4=2019,
解得:n=403.
故选:D.
【点评】此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.
11.如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(x1,0),且﹣1<x1<0,对称轴x=1.有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c>3b;⑤a+b>m(am+b)(m是不等于1的实数).其中结论正确个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据函数图象和二次函数的性质可以判断题目中各个小题的结论是否成立,从而可以解答本题.
【解答】解:①由图象可知:a<0,b>0,c>0,abc<0,故此选项错误;
②当x=﹣1时,y=a﹣b+c<0,即b>a+c,故此选项错误;
③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故此选项正确;
④当x=3时函数值小于0,y=9a+3b+c<0,且x=﹣=1,
即a=﹣,代入得9×(﹣)+3b+c<0,得2c<3b,故此选项错误;
⑤当x=1时,y的值最大.
所以a+b+c>am2+bm+c(m是不等于1的实数),
故a+b>am2+bm,即a+b>m(am+b),故此选项正确.
故③⑤正确.
故选:B.
【点评】本题考查了图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定.
12.若关于x的一元一次不等式组的解集为x≥2,且关于y的分式方程=1的解为非负整数,则所有满足条件的整数a的值之和是( )
A.4 B.5 C.11 D.12
【分析】由关于x的一元一次不等式组的解集为x≥2可得a<7,关于y的分式方程=1的解为y=,关于y的分式方程=1的解为非负数,可得a≥﹣3,由于分式方程有可能产生增根,所以,a≠1,综上,a的取值范围为﹣3≤a<7且a≠1,由于为整数,可得a=﹣3或﹣1或3或5,所有满足条件的整数a的值之和可求.
【解答】解:∵关于x的一元一次不等式组的解集为x≥2,
∴a﹣5<2.
∴a<7.
∵关于y的分式方程=1的解为y=,
又关于y的分式方程=1的解为非负数,
∴.
∴a≥﹣3.
∵由于分式方程=1有可能产生增根,
∴,
∴a≠1.
综上,a的取值范围为:﹣3≤a<7且a≠1.
∵为整数,
∴a=﹣3或﹣1或3或5.
∴所有满足条件的整数a的值之和为:﹣3﹣1+3+5=4.
故选:A.
【点评】本题主要考查了分式方程的解,一元一次不等式组的解集,有理数的混合运算.考虑解分式方程可能产生增根是解题的关键.
二.填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.
13.点P(﹣3,﹣4)关于原点对称的点的坐标是 (3,4) .
【分析】根据两个点关于原点对称时,它们的坐标符号相反,可以直接得到答案.
【解答】解:点P(﹣3,﹣4)关于原点对称的点的坐标是(3,4),
故答案为:(3,4).
【点评】本题主要考查了关于原点对称的点的坐标特点,两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y).
14.已知关于x的方程x2+3x+a=0有一个根为﹣2,则a= 2 .
【分析】把x=﹣2代入x2+3x+a=0中得到关于a的方程,然后解此方程即可.
【解答】解:把x=﹣2代入x2+3x+a=0得4﹣6+a=0,解得a=2.
故答案为2.
【点评】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.
15.若x﹣2y=5,则代数式5﹣2x+4y= ﹣5 .
【分析】将x﹣2y=5代入原式=5﹣2(x﹣2y)计算可得.
【解答】解:当x﹣2y=5时,原式=5﹣2(x﹣2y)=5﹣2×5=﹣5,
故答案为:﹣5.
【点评】本题主要考查代数式求值,解题的关键是熟练掌握整体代入思想的运用.
16.如图,在矩形ABCD中,BC=1,以点A为圆心,以AD长为半径画弧交BC于点E,∠DAE=60°,则图中阴影部分的面积为 ﹣ .
【分析】根据S阴=S矩形ABCD﹣S扇形ADE求解即可.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=1,AD∥BC,
∴∠AEB=∠DAE=60°,
∵∠B=90°,AE=AD=1,
∴AB=AE•sin60°=,
∴S阴=S矩形ABCD﹣S扇形ADE=﹣=﹣,
故答案为﹣.
【点评】本题考查了矩形的性质、扇形的面积公式和直角三角形的性质等知识点,能求出AB长和∠AEB的度数是解此题的关键.
17.如图,在正方形ABCD中,AB=4,点M在CD边上,且DM=1,△AEM与△ADM关于AM所在直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为 5 .
【分析】连接BM.先判定△FAE≌△MAB(SAS),即可得到EF=BM.再根据BC=CD=AB=4,CM=3,利用勾股定理即可得到,Rt△BCM中,BM=5,进而得出EF的长.
【解答】解:如图,连接BM.
∵△AEM与△ADM关于AM所在的直线对称,
∴AE=AD,∠MAD=∠MAE.
∵△ADM按照顺时针方向绕点A旋转90°得到△ABF,
∴AF=AM,∠FAB=∠MAD.
∴∠FAB=∠MAE,
∴∠FAB+∠BAE=∠BAE+∠MAE.
∴∠FAE=∠MAB.
∴△FAE≌△MAB(SAS).
∴EF=BM.
∵四边形ABCD是正方形,
∴BC=CD=AB=4.
∵DM=1,
∴CM=3.
∴在Rt△BCM中,BM==5,
∴EF=5,
故答案为:5.
【点评】本题考查了正方形的性质,勾股定理,全等三角形的判定与性质以及旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
18.为了践行“金山银山,不如绿水青山”的环保理念.重外环保小组的孩子们参与社区公益活动﹣收集废旧电池.活动开展一个月后,经过统计发现,全组成员平均每人收集了36颗废旧电池.其中,收集数量低于30颗的同学平均每人收集了28颗,收集数量不低于30颗的同学平均每人收集了42颗.数学王老师发现,若每人再多收集5颗,则收集数量低于30颗的同学平均每人收集了29颗,收集数量不低于30颗的同学平均每人收集了45颗并且该环保小组的人数介于40至60人.则该环保小组有 56 人.
【分析】设收集数量低于30颗的有x人,收集数量不低于30颗的有y人,根据收集的废旧电池数不变,即可得出关于x,y的二元一次方程,解之可得出x=y,进而可得出x+y=y,结合x,y均为正整数可得出(x+y)为7的倍数,设每人再多收集5颗时,收集数量低于30颗的有m人,则收集数量不低于30颗的有(x+y﹣m)人,根据收集的废旧电池数不变,即可得出关于(x+y),m的二元一次方程(将x+y当成整体),解之可得出x+y=4m,结合m为正整数可得出(x+y)为4的倍数,进而可得出(x+y)为28的倍数,再结合该环保小组的人数介于40至60人,即可求出(x+y)的值.
【解答】解:设收集数量低于30颗的有x人,收集数量不低于30颗的有y人,
依题意,得:28x+42y=36(x+y),
∴x=y,
∴x+y=y.
∵x,y均为正整数,
∴(x+y)为7的倍数,y为4的倍数.
设每人再多收集5颗时,收集数量低于30颗的有m人,则收集数量不低于30颗的有(x+y﹣m)人,
依题意,得:29m+45(x+y﹣m)=(36+5)(x+y),
∴x+y=4m.
∵m为正整数,
∴(x+y)为4的倍数,
∴(x+y)为28的倍数.
又∵该环保小组的人数介于40至60人,
∴x+y=28×2=56.
故答案为:56.
【点评】本题考查了二元一次不定方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
三.解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
19.(10分)(1)解方程:2x2﹣3x+1=0;
(2)化简:÷(+m﹣1).
【分析】(1)直接用十字相乘法分解求值即可;
(2)除式先通分再化简,最后再算除法.
【解答】解:(1)(2x﹣1)(x﹣1)=0,
2x﹣1=0或x﹣1=0,
解得x1=,x2=1;
(2)原式=:÷[+]
=÷
=÷
=1.
【点评】本题考查了一元二次方程的因式分解法、分式的混合运算等知识点,掌握因式分解的十字相乘法和分式的混合运算是解决本题的关键.
20.(10分)如图,在直角坐标系中,点A,B,C的坐标分别为(3,3),(4,0),(0,2),将△ABC绕着点C顺时针旋转90°得△A1B1C,其中点A的对应点为点A1.
(1)请画出旋转后的△A1B1C,并写出A1的坐标;
(2)求出在旋转过程中点A所走过的路径长.(结果保留π)
【分析】(1)利用旋转变换的性质分别作出A,B的对应点A1,B1即可;
(2)利用弧长公式求解.
【解答】解:(1)如图,△A1B1C即为所求,A1(1,﹣1);
(2)∵CA==,
∴点A所走过的路径长==π.
【点评】本题考查作图﹣旋转变换,轨迹等知识,解题的关键是掌握旋转变换的性质,属于中考常考题型.
21.(10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连接AC,若CA=CP,∠A=30°.
(1)求证:CP是⊙O的切线;
(2)若OA=1,求弦AC的长.
【分析】(1)连接OC,由等腰三角形的性质得出∠A=∠ACO=30°,∠P=30°,求出∠ACP的度数,则可求出答案;
(2)连接BC,由勾股定理可求出答案.
【解答】(1)证明:连接OC,如图,
∵OA=OC,∠A=30°,
∴∠A=∠ACO=30°,
∵CA=CP,
∴∠A=∠P=30°,
∴∠ACP=180°﹣∠A﹣∠P=180°﹣30°﹣30°=120°,
∴∠OCP=∠ACP﹣∠ACO=120°﹣30°=90°,
∴OC⊥CP,
∴CP是⊙O的切线;
(2)解:如图,连接BC,
∵OA=OB=1,
∴AB=2,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=30°,
∴BC=AB=1,
∴AC==.
【点评】本题考查了切线的判定,等腰三角形的性质,勾股定理,圆周角定理,直角三角形的性质,熟练掌握切线的判定是解题的关键.
22.(10分)借鉴我们已有研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象与性质,研究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣2
﹣1
0
1
2
3
4
5
…
y
…
10
m
﹣2
1
n
1
﹣2
3
10
…
其中,m= 3 ,n= 2 ;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①写出函数的一条图象性质: 图象具有对称性,对称轴是直线x=1 ;
②当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出b的取值范围为 b=﹣2或b>2 .
【分析】(1)把x=﹣2和x=1分别代入y=|x2﹣2x﹣3|﹣2,即可求得;
(2)描点、连线画出图形;
(3)①根据图象即可求得;
②根据图象即可求得.
【解答】解:(1)把x=﹣2代入y=|x2﹣2x﹣3|﹣2,得y=3,
∴m=3,
把x=1代入y=|x2﹣2x﹣3|﹣2,得y=2,
∴n=2,
故答案为:3,2;
(2)如图所示;
(3)①函数的性质:图象具有对称性,对称轴是直线x=1;
故答案为图象具有对称性,对称轴是直线x=1:
②由图象可知,当b=﹣2或b>2时,函数y=|x2﹣2x﹣3|﹣2图象与直线y=b有两个交点,
∵当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根时,b=﹣2或b>2,
故答案为b=﹣2或b>2.
【点评】本题考查了二次函数与x轴的交点问题和一元二次方程的根的情况,注意利用数形结合的思想,理解一元二次方程与抛物线的关系是解此题的关键.
23.(10分)为了创建国家级卫生城区,某社区在九月份购买了甲、乙两种绿色植物共1100盆,共花费了27000元.已知甲种绿色植物每盆20元,乙种绿色植物每盆30元.
(1)该社区九月份购买甲、乙两种绿色植物各多少盆?
(2)十月份,该社区决定再次购买甲、乙两种绿色植物.已知十月份甲种绿色植物每盆的价格比九月份的价格优惠元(a>0),十月份乙种绿色植物每盆的价格比九月份的价格优惠a%.因创卫需要,该社区十月份购买甲种绿色植物的数量比九月份的数量增加了a%,十月份购买乙种绿色植物的数量比九月份的数量增加a%.若该社区十月份的总花费与九月份的总花费恰好相同,求a的值.
【分析】(1)设该社区九月份购买甲种绿色植物x盆,购买乙种绿色植物y盆,根据“该社区在九月份购买了甲、乙两种绿色植物共1100盆,共花费了27000元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据总价=单价×数量结合该社区十月份的总花费与九月份的总花费恰好相同,即可得出关于a的一元二次方程,解之取其正值即可得出结论.
【解答】解:(1)设该社区九月份购买甲种绿色植物x盆,购买乙种绿色植物y盆,
依题意,得:,
解得:.
答:该社区九月份购买甲种绿色植物600盆,购买乙种绿色植物500盆.
(2)依题意,得:(20﹣)×600(1+a%)+30(1﹣a%)×500(1+a%)=27000,
整理,得:1.2a2﹣30a=0,
解得:a1=25,a2=0(不合题意,舍去).
答:a的值为25.
【点评】本题考查了二元一次方程组的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
24.(10分)若在一个三位自然数中,十位上的数字恰好等于百位与个位上的数字之和,则称这个三位数为“奇异数”.例如,在自然数132中,3=1+2,则132是“奇异数”;在自然数462中,6=4+2,则462是“奇异数”.
(1)请你写出最大的“奇异数”,并证明:任意一个“奇异数”一定能被11整除.
(2)若有“奇异数”能同时被3和7整除,求出这样的“奇异数”.
【分析】(1)依据“奇异数”的定义可写出最大的“奇异数”;用代数式表示出“奇异数”,利用因式分解法进行证明;
(2)利用“奇异数”的定义和已知,结合数位的数字特征解答.
【解答】解:(1)∵作为数位上的数字,9最大,
∴把9放在百位.
∵“奇异数”的十位上的数字恰好等于百位与个位上的数字之和,
∴个位只能是0.
∴最大的“奇异数”是990.
证明:设一个“奇异数”的百位数字是a,个位数字是b,则十位数字为a+b,
其中a,b为整数,1≤a≤9,0≤b≤9,a+b≤9,
∴这个“奇异数”为:100a+10(a+b)+b.
∵100a+10(a+b)+b
=100a+10a+10b+b
=110a+11b
=11(10a+b),
∴任意一个“奇异数”一定能被11整除.
(2)由(1)可知,任意的一个“奇异数”都可以表示成11(10a+b)的形式.
∵若“奇异数”能同时被3和7整除,
∴10a+b是21的倍数.
∵a,b为整数,1≤a≤9,0≤b≤9,a+b≤9,
∴a=2,b=1或a=4,b=2或a=6,b=3.
∴能同时被3和7整除的“奇异数”有:231,462,693.
【点评】本题主要考查了因式分解的应用,本题是阅读型题目,准确理解题干中的定义并熟练应用是解题的关键.
25.(10分)综合与探究
在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交点C.
(1)求抛物线与直线AC的函数解析式;
(2)若点P是直线AC上方抛物线上的一动点,过点P作PF⊥x轴于点F,交直线AC于点D,求线段PD的最大值.
(3)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
【分析】(1)应用待定系数法即可求出抛物线解析式,再求出点C的坐标,设直线AC的解析式为y=kx+2,将点C的坐标代入即可求得答案;
(2)如图1,设点,则,则==,应用二次函数最值即可求得答案;
(3)分两种情况:①若CM平行于x轴,如图2,有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.②若CM不平行于x轴,如图所示,过点M作MG⊥x轴于G,易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=﹣2,设M(x,﹣2),建立方程求解即可.
【解答】解:(1)∵二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,
∴,
解得:,
∴这个二次函数的解析式为;
∵二次函数与y轴交于点C,
∴点C的坐标为(0,2),
设直线AC的解析式为y=kx+2,
∵直线AC经过点A(﹣3,0),
∴0=﹣3k+2,
解得:,
∴直线AC的解析式为;
(2)由(1)得,
如图1,设点,则,
∴==,
∴当时,PD最大,最大值是.
(3)存在.假设存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形.
①若CM平行于x轴,如图2,有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.
∵CM∥x轴,
∴点M、点C(0,2)关于对称轴x=﹣1对称,
∴M(﹣2,2),
∴CM=2,
由Q1A=Q2A=CM=2,得到Q1(﹣5,0),Q2(﹣1,0);
②若CM不平行于x轴,如图所示,过点M作MG⊥x轴于G,
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=﹣2,
设M(x,﹣2),则有,
解得:,
又QG=3,
∴,
∴,.
综上所述,存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形.Q点坐标为:Q1(﹣5,0),Q2(﹣1,0),,.
【点评】本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、二次函数最值应用等,其中(3),要注意分类求解,避免遗漏.
四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.(8分)如图,在边长为6的等边△ABC中,点E为边BC上任意一点,连接AE将线段AE绕点A逆时针旋转60°,点E的对应点是点D,连接ED、CD.
(1)如图1,求证:EC+CD=AB;
(2)如图2,在旋转过程中,取AE、CD的中点F、G,连接FG和FC,当AE⊥BC时,试猜想FG与FC的大小关系,写出你猜想的关系式,并证明;
(3)如图2,在整个旋转过程中,FG的长度是否发生变化,若不变化,直接写出FG的值,若变化,请直接写出FG的取值范围.
【分析】(1)根据SAS证△ABE≌△ACD,即可得证CD=BE,又AB=BC,即可得证结论;
(2)取AD的中点H,连接HF,HG,BF,根据三角形的中位线定理得HG=AC,FH=ED,根据SAS证△BEF≌△GHF,得出FB=FG,又FB=FC,故FG=FC;
(3)先判断当E点与B点重合时FG有最大值,当E点与C点重合时FG有最小值求出FG的取值范围即可.
【解答】解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC=BC,
由旋转可知,AE=AD,∠EAD=60°,
∴∠BAC=∠EAD,
∴∠BAE+∠EAC=∠EAC+∠CAD,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD,
∴BC=BE+EC=CD+EC,
∴AB=EC+CD;
(2)FG=FC,
理由:取AD的中点H,连接HF,HG,BF,
∵等边三角形ABC,AE⊥BC,点E是BC的中点,
∴∠CAE=∠BAC=30°,∠FEB=90°,FB=FC,
∵∠EAD=60°,AD=AE,
∴∠CAD=30°,△ADE是等边三角形,
∴DE=AE,∠ADE=60°,
∵点H是AD的中点,点F是AE的中点,点G是CD的中点,
∴FG∥AC,HG=AC,FH∥ED,FH=ED,
∴∠DHG=∠DAC=30°,∠AHF=∠ADE=60°,FH=EF,GH=BE,
∴∠FHG=∠BEF=90°,
在△BEF和△GHF中,
,
∴△BEF≌△GHF(SAS),
∴FB=FG,
∵AE⊥BC,点E是BC的中点,
∴FB=FC,
∴FG=FC;
(3)FG长度发生变化,3≤FG≤3,
理由:当点E与点B重合时,则点G与点C重合,此时FG最长,如下图,
∵△ABC是等边三角形,点F是AE的中点,
∴AF=AB=×6=3,
∴FG===3,
当点E与点C重合时,此时FG最短,如下图,
∵点F是AE的中点,点G是CD的中点,
∴FG=AD=AC=×6=3,
∴3≤FG≤3.
【点评】本题主要考查图形的旋转变换,涉及全等三角形的判定和性质,三角形的中位线,等边三角形的性质等知识,熟练掌握全等三角形的判定和性质及等边三角形的性质是解题的关键.
重庆市綦江区古南中学2023-2024学年八年级上学期入学数学试卷: 这是一份重庆市綦江区古南中学2023-2024学年八年级上学期入学数学试卷,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
重庆市綦江区古南中学2023-2024学年八年级上学期入学测试数学试题: 这是一份重庆市綦江区古南中学2023-2024学年八年级上学期入学测试数学试题,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年重庆市綦江区古南中学七年级(上)第一次月考数学试卷(解析版): 这是一份2022-2023学年重庆市綦江区古南中学七年级(上)第一次月考数学试卷(解析版),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












