数学必修 第一册7.1 角与弧度图片ppt课件

7.1.2　弧度制

在初中，我们是如何求一个扇形的弧长的？在弧长公式中，角α是如何度量的？度量的单位是什么？它的1个单位是怎么定义的？用这种单位制来度量角叫做什么制？除了上面用“度”作为单位来度量角的角度外，我们有没有其他的方式来度量角呢？

知识点1　弧度制的概念

(1)角度制：规定周角的为1度的角，用度作为单位来度量角的单位制叫作角度制．

(2)弧度制：把长度等于半径长的弧所对的圆心角叫作1弧度的角，记作1 rad，用弧度作为角的单位来度量角的单位制称为弧度制．

1.“1弧度的角”的大小和所在圆的半径大小有关系吗？

[提示]　“1弧度的角”是一个定值，与所在圆的半径大小无关．

2.比值与所取的圆的半径大小是否有关？

[提示]　一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的，与半径大小无关．

1.思考辨析(正确的打“√”，错误的打“×”)

(1)大圆中1弧度角比小圆中1弧度角大．(　　)

(2)圆心角为1弧度的扇形的弧长都相等．(　　)

(3)长度等于半径的弦所对的圆心角是1弧度．(　　)

[答案]　(1)×　(2)×　(3)×

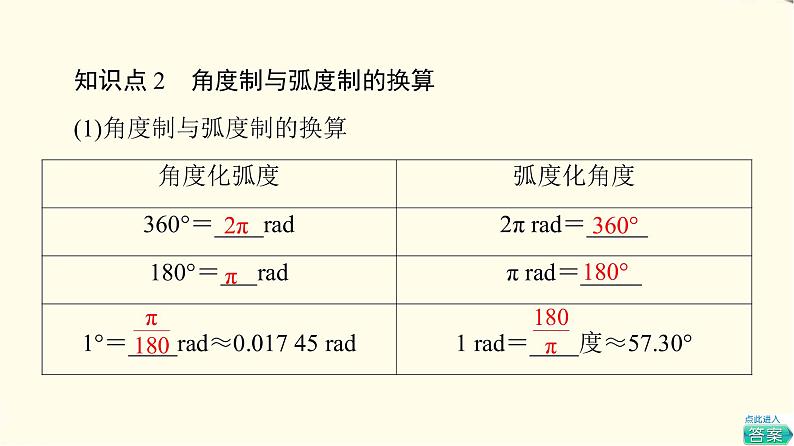
知识点2　角度制与弧度制的换算

(1)角度制与弧度制的换算

(2)一些特殊角的度数与弧度数的对应关系

(3)任意角的弧度数与实数的对应关系

正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是0.

3.角度制与弧度制之间如何进行换算？

[提示]　利用1°＝rad≈0.017 45 rad和1 rad＝°≈57.30°进行弧度与角度的换算．

2.将下列弧度与角度互化．

(1)化为角度为________；

(2)105°化为弧度为________．

(1)252°　(2)　[(1)π＝°＝252°.

(2)105°＝105°× rad＝ rad.]

知识点3　扇形的弧长公式及面积公式

(1)弧度制下的弧长公式：

如图，l是圆心角α所对的弧长，r是半径，则圆心角α的弧度数的绝对值是|α|＝，弧长l＝|α|r.特别地，当r＝1时，弧长l＝|α|.

(2)扇形面积公式：

在弧度制中，若|α|≤2π，则半径为r，圆心角为α的扇形的面积为S＝·πr2＝lr.

(3)引入弧度制的意义

角的概念的推广后，角的集合与弧度数的集合之间建立了一一对应关系，即角的集合与实数集R之间建立了一一对应关系；每一个角都对应唯一的一个实数，反过来，每一个实数也都对应唯一的一个角，为以后三角函数的建立奠定了基础．

3.半径为1，圆心角为的扇形的弧长为______，面积为________．

　　[∵α＝，r＝1，

∴弧长l＝α·r＝，

面积＝lr＝××1＝.]

类型1　角度制与弧度制的互化

【例1】　把下列弧度化成角度或角度化成弧度：

(1)－450°；(2)；(3)－；(4)112°30′.

[解]　(1)－450°＝－450× rad＝－ rad.

(2) rad＝×＝18°.

(3)－ rad＝－×＝－240°.

(4)112°30′＝112.5°＝112.5× rad＝ rad.

角度制与弧度制换算的要点

提醒：角度化弧度时，应先将分、秒化成度，再把角度化成弧度．

[跟进训练]

1．将下列角度与弧度进行互化．

(1)π　(2)　(3)－1440°　(4)67°30′

[解]　(1)π rad＝π×＝108°.

(2) rad＝×＝15°.

(3)－1440°＝－1440×＝－8π.

(4)67°30′＝67.5°＝67.5×＝π.

类型2　用弧度制表示角的集合

【例2】　用弧度制表示顶点在原点，始边重合于x轴的非负半轴，终边落在阴影部分内的角的集合(不包括边界，如图所示)．

[解]　(1).

(2).

(3).

1．弧度制下与角α终边相同的角的表示

在弧度制下，与角α的终边相同的角可以表示为{β|β＝2kπ＋α，k∈Z}，即与角α终边相同的角可以表示成α加上2π的整数倍．

2．根据已知图形写出区域角的集合的步骤

(1)仔细观察图形．

(2)写出区域边界作为终边时角的表示．

(3)用不等式表示区域范围内的角．

提醒：角度制与弧度制不能混用．

[跟进训练]

2．用弧度制表示终边在图中阴影区域内角的集合(包括边界)，并判断2 024°是不是这个集合的元素．

[解]　因为150°＝，

所以终边在阴影区域内角的集合为

S＝

因为2 024°＝224°＋5×360°＝ rad，

又<<.

所以2 024°＝∈S.

类型3　扇形的弧长及面积问题

【例3】　已知扇形的周长为8 cm.

(1)若该扇形的圆心角为2 rad，求该扇形的面积；

(2)求该扇形的面积的最大值，并指出对应的圆心角．

[解]　设扇形的半径为r，弧长为l，扇形面积为S.

(1)由题意得：2r＋l＝8，l＝2r，

解得r＝2，l＝4，S＝lr＝4.

(2)由2r＋l＝8得l＝8－2r，r∈(0,4)，

则S＝lr＝(8－2r)r＝4r－r2＝－(r－2)2＋4，

当r＝2时，Smax＝4，此时l＝4，圆心角α＝＝2.

1．(变条件，变结论)本例条件下，若扇形面积为3 cm2，求扇形的圆心角的弧度数．

[解]　设扇形的半径为r，弧长为l，圆心角为α，

扇形面积为S.

由题意得：

解得l＝6，r＝1或l＝2，r＝3，

所以α＝＝6或.

2．(变条件，变问法)本例条件中“周长为8 cm”改为“面积为8 cm2”，在(1)的条件下求该扇形的弧长．

[解]　设扇形的半径为r，弧长为l，扇形的面积为S，则由

S＝·α·r2得8＝×2×r2，

所以r＝2，

所以l＝αr＝2×2＝4(cm)．

弧度制下有关扇形弧长、面积问题的解题策略及其注意点

(1)解题策略：

①明确弧度制下扇形弧长公式l＝|α|r，扇形的面积公式S＝lr＝|α|r2(其中l是扇形的弧长，α是扇形的圆心角)．

②涉及扇形的周长、弧长、圆心角、面积等的计算，关键是先分析题目已知哪些量求哪些量，然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解．

(2)注意点：

①在弧度制中的弧长公式及扇形面积公式中的圆心角可正可负．

②看清角的度量制，选用相应的公式．

③扇形的周长等于弧长加两个半径长．

[跟进训练]

3．已知扇形OAB的周长是10 cm，面积为4 cm2，求扇形OAB的圆心角的弧度数．

[解]　设扇形圆心角的弧度数为θ(0<θ<2π)，弧长为l，半径为r.

依题意有，由①得l＝10－2r，代入②得r2－5r＋4＝0，

解得r1＝1，r2＝4.当r＝1时，l＝8(cm)，此时θ＝8 rad>2π(舍去)，

当r＝4时，l＝2(cm)，此时θ＝＝ rad.

所以扇形OAB的圆心角的弧度数为 rad.

1．(多选题)下列转化结果正确的是(　　)

A．60°化成弧度是

B．－π化成度是－600°

C．－150°化成弧度是－π

D．化成度是15°

ABD　[对于A,60°＝60×＝；对于B，－π＝－×180°＝－600°；对于C，－150°＝－150×＝－π；对于D，＝×180°＝15°.故ABD正确．]

2．已知α＝－2 rad，则角α的终边在(　　)

A．第一象限 B．第二象限

C．第三象限 D．第四象限

C　[α＝－2 rad≈－2·57.30°＝－115°，在第三象限．]

3．半径为1，圆心角为的扇形的面积是(　　)

A． B．π

C． D．

D　[S＝lr＝r2α＝×12×＝.]

4．若把－570°写成2kπ＋α(k∈Z,0≤α<2π)的形式，则α＝________.

　[－570°＝－＝－4π＋.]

5．若扇形的周长为4 cm，面积为1 cm2，则扇形的半径为________cm，圆心角的弧度数为________．

1　2　[设扇形所在圆的半径为r cm，扇形弧长为l cm.

由题意得

解得

所以α＝＝2.

因此扇形的圆心角的弧度数是2，半径为1 cm.]

回顾本节知识，自我完成以下问题．

1．弧度制与角度制互化公式是什么？

[提示]　1 rad＝°，10＝ rad.

2．角度制与弧度制互化的关键与方法是什么？

[提示]　关键：抓住互化公式π rad＝180°，

方法：度数×＝弧度数，

弧度数×°＝度数．

3．若角度中含有分、秒该如何化为弧度？

[提示]　应先将分、秒化成度，再化成弧度．

4．在表示终边相同的角时应注意什么问题？

[提示]　角度与弧度不能混用．在表示角时要么全部用弧度制，要么全部用角度制．