

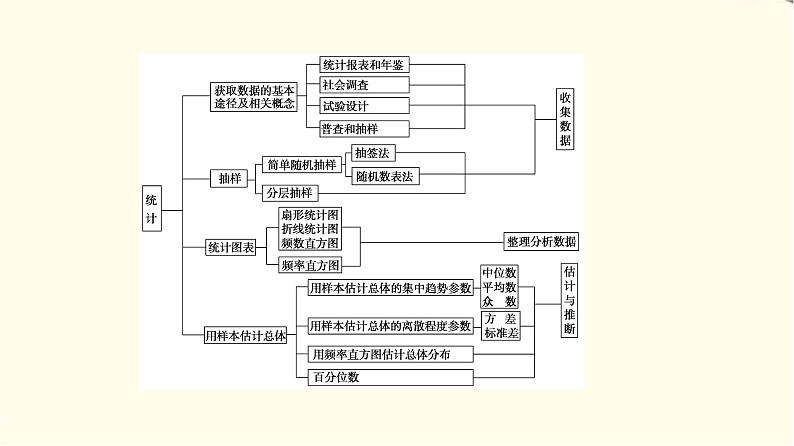





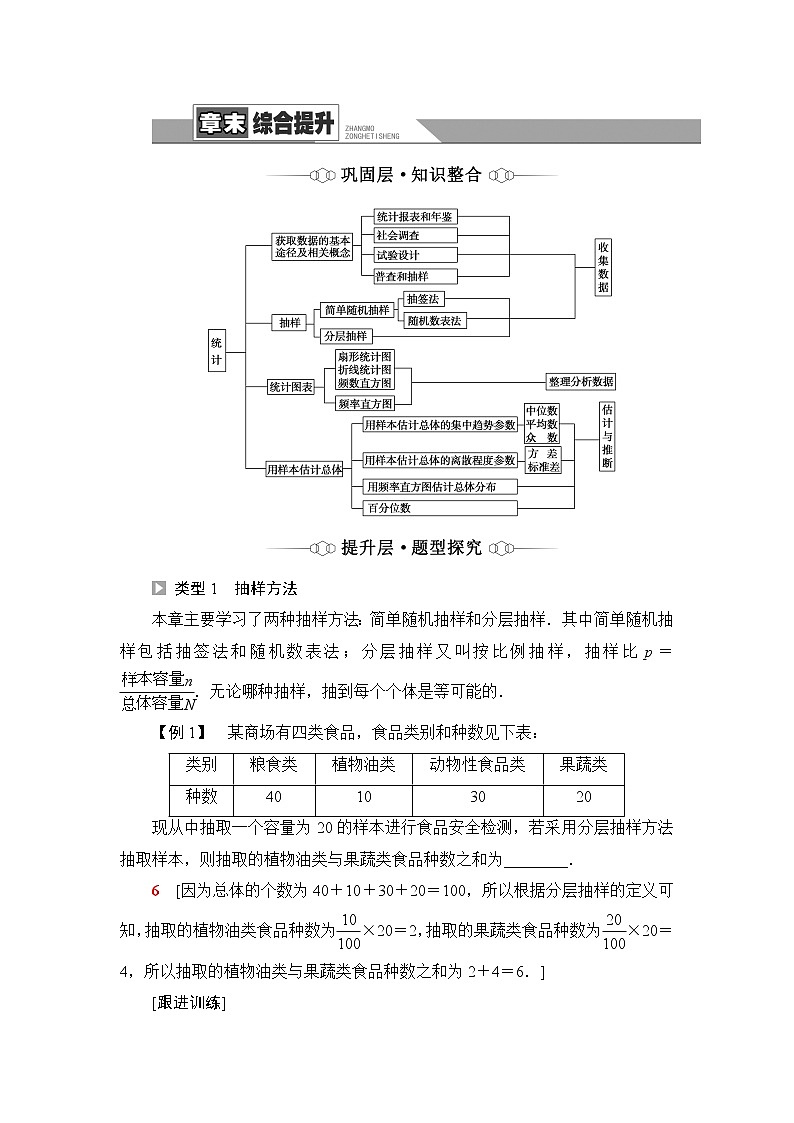

苏教版高中数学必修第二册第14章章末综合提升课件+学案
展开类型1 抽样方法
本章主要学习了两种抽样方法:简单随机抽样和分层抽样.其中简单随机抽样包括抽签法和随机数表法;分层抽样又叫按比例抽样,抽样比p=.无论哪种抽样,抽到每个个体是等可能的.
【例1】 某商场有四类食品,食品类别和种数见下表:
类别 | 粮食类 | 植物油类 | 动物性食品类 | 果蔬类 |
种数 | 40 | 10 | 30 | 20 |
现从中抽取一个容量为20的样本进行食品安全检测,若采用分层抽样方法抽取样本,则抽取的植物油类与果蔬类食品种数之和为________.
6 [因为总体的个数为40+10+30+20=100,所以根据分层抽样的定义可知,抽取的植物油类食品种数为×20=2,抽取的果蔬类食品种数为×20=4,所以抽取的植物油类与果蔬类食品种数之和为2+4=6.]
[跟进训练]
1.从30个个体(编号为00~29)中抽取10个样本,现给出某随机数表的第11行到第15行(见下表),如果某人选取第12行的第6列和第7列的数作为第一个数并且由此数向右读,则选取的前4个的号码分别为________.
9264 4607 2021 3920 7766 3817 3256 1640
5858 7766 3170 0500 2593 0545 5370 7814
2889 6628 6757 8231 1589 0062 0047 3815
5131 8186 3709 4521 6665 5325 5383 2702
9055 7196 2172 3207 1114 1384 4359 4488
17,00,02,07 [在随机数表中,将处于00~29的号码选出,满足要求的前4个号码为17,00,02,07.]
2.利用简单随机抽样,从n个个体中抽取一个容量为10的样本.若第二次抽取时,余下的每个个体被抽到的概率为,则在整个抽样过程中,每个个体被抽到的概率为________.
[根据题意,=,解得n=28.
故在整个抽样过程中每个个体被抽到的概率为=.]
类型2 用样本的频率估计总体分布
(1)频率=,已知其中任意两个量就可以求出第三个量.
(2)各小组的频数和等于样本容量,频率和等于1.
(3)由样本的频率可估计总体的频率,从而估计出总体的频数.
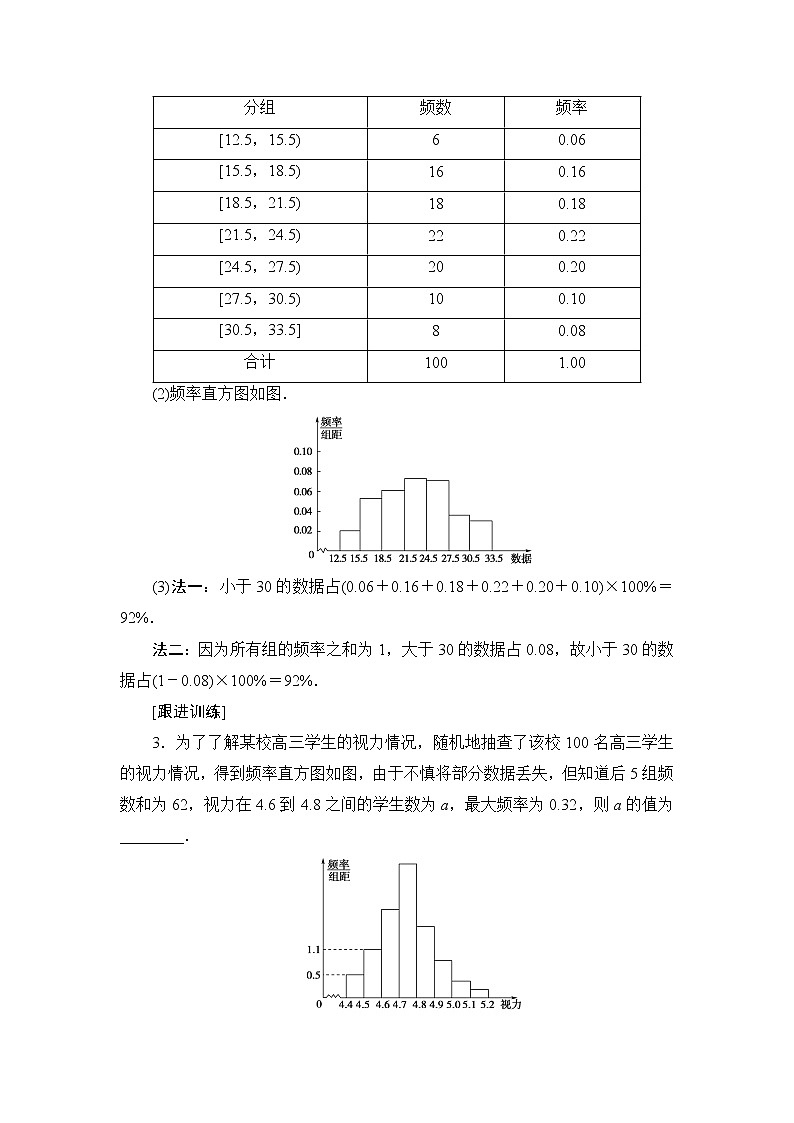
【例2】 有1个容量为100的样本,数据(均为整数)的分组及各组的频数如下:
[12.5,15.5),6;[15.5,18.5),16;[18.5,21.5),18;[21.5,24.5),22;[24.5,27.5),20;[27.5,30.5),10;[30.5,33.5],8.
(1)列出样本的频率分布表;
(2)画出频率直方图;
(3)估计数据小于30的数据约占的百分比.
[解] (1)样本的频率分布表如下:
分组 | 频数 | 频率 |
[12.5,15.5) | 6 | 0.06 |
[15.5,18.5) | 16 | 0.16 |
[18.5,21.5) | 18 | 0.18 |
[21.5,24.5) | 22 | 0.22 |
[24.5,27.5) | 20 | 0.20 |
[27.5,30.5) | 10 | 0.10 |
[30.5,33.5] | 8 | 0.08 |
合计 | 100 | 1.00 |
(2)频率直方图如图.
(3)法一:小于30的数据占(0.06+0.16+0.18+0.22+0.20+0.10)×100%=92%.
法二:因为所有组的频率之和为1,大于30的数据占0.08,故小于30的数据占(1-0.08)×100%=92%.
[跟进训练]
3.为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率直方图如图,由于不慎将部分数据丢失,但知道后5组频数和为62,视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为________.
54 [[4.7,4.8)之间频率为0.32,[4.6,4.7)之间频率为1-0.62-0.05-0.11=1-0.78=0.22.
所以a=(0.22+0.32)×100=54.]
4.为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如表1,表2.
表1:男生身高频数分布表
身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生身高频数分布表
身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180] |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求该校男生的人数并画出频率直方图;
(2)估计该校学生身高在165 cm~180 cm的人数占总人数的百分比.
[解] (1)样本中男生人数为40,分层抽样比例为10%,可得全校男生人数为400.频率直方图如图.
(2)由表1、表2知,样本中身高在165 cm~180 cm的学生人数为5+14+13+6+3+1=42,样本容量为70,所以样本中学生身高在165 cm~180 cm的频率为=,故估计该校学生身高在165 cm~180 cm的人数占总人数的60%.
类型3 用样本的特征数估计总体的特征数
样本的特征数可分为两大类:一类是反映样本数据集中趋势的,包括众数、中位数和平均数;另一类是反映样本波动大小的,包括方差及标准差.我们常通过样本的特征数估计总体的特征数.
【例3】 甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为
甲:99,100,98,100,100,103;
乙:99,100,102,99,100,100.
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
[解] (1)甲=(99+100+98+100+100+103)=100,
乙=(99+100+102+99+100+100)=100.
s=[(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+(103-100)2]=,
s=[(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+(100-100)2]=1.
(2)两台机床所加工零件的直径的平均数相同,又s>s,
所以乙机床加工零件的质量更稳定.
[跟进训练]
5.有容量为100的样本,数据分组及各组的频数、频率如下:
[12.5,14.5),6,0.06;[14.5,16.5),16,0.16;[16.5,18.5),18,0.18;[18.5,20.5),22,0.22;[20.5,22.5),20,0.20;[22.5,24.5),10,0.10;[24.5,26.5],8,0.08.
试估计总体的平均数.
[解] 法一:总体的平均数约为
×(13.5×6+15.5×16+17.5×18+19.5×22+21.5×20+23.5×10+25.5×8)=19.42.
故总体的平均数约为19.42.
法二:求组中值与对应频率积的和
13.5×0.06+15.5×0.16+17.5×0.18+19.5×0.22+21.5×0.20+23.5×0.10+25.5×0.08=19.42.
故总体的平均数约为19.42.
6.对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩好?谁的各门功课发展较平衡?
[解] 甲的平均成绩为甲=74,乙的平均成绩为乙=73.所以甲的平均成绩好.
甲的方差是s=×[(-14)2+62+(-4)2+162+(-4)2]=104,乙的方差是s=×[72+(-13)2+(-3)2+72+22]=56.
因为s>s,所以乙的各门功课发展较平衡.
1.(多选题)(2020·新高考全国卷Ⅱ)我国新冠肺炎疫情防控进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
A.这11天复工指数和复产指数均逐日增加
B.这11天期间,复产指数增量大于复工指数的增量
C.第3天至第11天复工复产指数均超过80%
D.第9天至第11天复产指数增量大于复工指数的增量
CD [由折线图知,第1天至第2天复工指数减少,第7天至第8天复工指数减少,第10天至第11天复工指数减少,第8天至第9天复产指数减少,故A错误;由折线图知,第1天的复产指数与复工指数的差大于第11天的复产指数与复工指数的差,所以这11天期间,复产指数增量小于复工指数的增量,故B错误;由折线图知,第3天至第11天复工复产指数均超过80%,故C正确;由折线图知,第9天至第11天复产指数增量大于复工指数的增量,故D正确.综上,选CD.]
2.(2020·天津高考)从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到如下频率直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )
A.10 B.18 C.20 D.36
B [由题知[5.43,5.45)与[5.45,5.47)所对应的小矩形的高分别为6.25,5.00,所以[5.43,5.47)的频率为(6.25+5.00)×0.02=0.225,所以直径落在区间[5.43,5.47)内的个数为80×0.225=18,故选B.]
3.(2020·全国卷Ⅲ)设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为( )
A.0.01 B.0.1 C.1 D.10
C [由方差计算公式:x1,x2,…,xn的方差为s2,所以s2=0.01,则ax1,ax2,…,axn的方差为a2s2,则所求为100s2=1.]
4.(2019·全国卷Ⅱ)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
A [记9个原始评分分别为a,b,c,d,e,f,g,h,i(按从小到大的顺序排列),易知e为7个有效评分与9个原始评分的中位数,故不变的数字特征是中位数,故选A.]
5.(2020·江苏高考)已知一组数据4,2a,3-a,5,6的平均数为4,则a的值是________.
2 [一组数据4,2a,3-a,5,6的平均数为4,则4+2a+(3-a)+5+6=4×5,解得a=2.]









