数学必修 第二册13.3 空间图形的表面积和体积课文内容ppt课件

这是一份数学必修 第二册13.3 空间图形的表面积和体积课文内容ppt课件，文件包含苏教版高中数学必修第二册第13章1331331空间图形的表面积课件ppt、苏教版高中数学必修第二册第13章1331331空间图形的表面积学案doc、苏教版高中数学必修第二册课后素养落实34空间图形的表面积含答案doc等3份课件配套教学资源，其中PPT共52页， 欢迎下载使用。
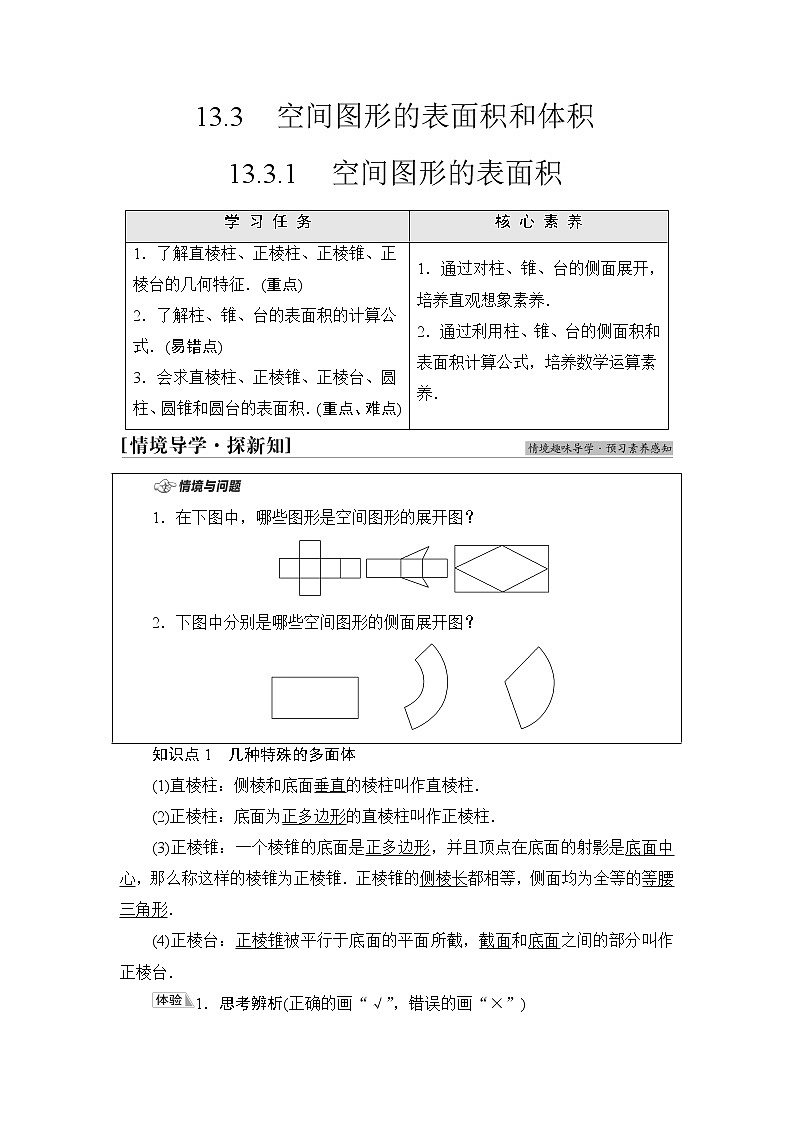
课后素养落实(三十四)　空间图形的表面积(建议用时：40分钟)一、选择题1．下列有四个结论，其中正确的是(　　)A．各个侧面都是等腰三角形的棱锥是正棱锥B．三条侧棱都相等的棱锥是正棱锥C．底面是正三角形的棱锥是正三棱锥D．顶点在底面上的射影既是底面多边形的内心，又是外心的棱锥必是正棱锥D　[A不正确，正棱锥必备两点，一是底面为正多边形，二是顶点在底面内的射影是底面的中心；B缺少第一个条件；C缺少第二个条件；而D可推出以上两个条件，故正确．]2．一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积之比为(　　)A．  B．  C．  D．A　[设圆柱的底面半径为r，高为h，则有h＝2πr，所以表面积与侧面积的比为2π(r2＋rh)∶2πrh＝(r＋h)∶h＝(2π＋1)∶2π．]3．轴截面是正三角形的圆锥称为等边圆锥，则等边圆锥的侧面积是底面积的(　　)A．4倍  B．3倍  C．倍  D．2倍D　[设轴截面正三角形的边长为2a，所以S底＝πa2，S侧＝πa×2a＝2πa2，所以S侧＝2S底． 故选D．]4．如图，在三棱柱ABC­A1B1C1中，AA1⊥底面ABC，AB⊥BC，AA1＝AC＝2，直线A1C与侧面AA1B1B所成的角为30°，则该三棱柱的侧面积为(　　)A．4＋4 B．4＋4C．12D．8＋4A　[连接A1B．因为AA1⊥底面ABC，则AA1⊥BC，又AB⊥BC，AA1∩AB＝A，所以BC⊥平面AA1B1B，所以直线A1C与侧面AA1B1B所成的角为∠CA1B＝30°．又AA1＝AC＝2，所以A1C＝2，BC＝．又AB⊥BC，则AB＝，则该三棱柱的侧面积为2××2＋2×2＝4＋4，故选A．]5．若某圆锥的高等于其底面直径，则它的底面积与侧面积之比为(　　)A．1∶2 　  B．1∶  C．1∶  D．∶2C　[设圆锥底面半径为r，则高h＝2r，∴其母线长l＝r．∴S侧＝πrl＝πr2，S底＝πr2，S底∶S侧＝1∶．]二、填空题6．斜三棱柱的底面是边长为5的正三角形，侧棱长为4，侧棱与底面两边所成角都是60°，那么这个斜三棱柱的侧面积是________．20＋20　[由题意可知S侧＝2×5×4×sin 60°＋5×4＝20＋20．]7．一个圆台的母线长等于上、下底面半径和的一半，且侧面积是32π，则母线长为________．4　[∵l＝，∴S侧＝π(R＋r)l＝2πl2＝32π，∴l＝4．]8．已知正三棱台的上底面边长为2，下底面边长为4，高为，则正三棱台的侧面积S1与底面积之和S2的大小关系为________．S1>S2　[斜高h′＝＝，S1＝×(3×2＋3×4)×＝9，S2＝×22＋×42＝5，∴S1>S2．]三、解答题9．圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积为392 cm2，母线与轴的夹角为45°，求这个圆台的高、母线长和底面半径．[解]　法一：圆台的轴截面如图所示，根据题意可设圆台的上、下底面半径分别为x cm和3x cm．即A′O′＝x cm，AO＝3x cm(O′，O分别为上、下底面圆心)，过A′作AB的垂线，垂足为点D．在Rt△AA′D中，∠AA′D＝45°，AD＝AO－A′O′＝2x cm，所以A′D＝AD＝2x cm，又S轴截面＝(A′B′＋AB)·A′D＝×(2x＋6x)×2x＝392(cm2)，所以x＝7．综上，圆台的高OO′＝14 cm，母线长AA′＝OO′＝14  cm，上、下底面的半径分别为7 cm和21 cm．法二：圆台的轴截面如图所示，根据题意可设圆台的上、下底面半径分别为x cm和3x cm，延长AA′，BB′交OO′的延长线于点S(O′，O分别为上、下底面圆心)．在Rt△SOA中，∠ASO＝45°，所以SO＝AO＝3x cm，又SO′＝A′O′＝x cm，所以OO′＝2x cm．又S轴截面＝×(2x＋6x)×2x＝392(cm2)，所以x＝7．综上，圆台的高OO′＝14 cm，母线长AA′＝OO′＝14 cm，上、下底面的半径分别为7 cm,21 cm．10．如图所示，正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截，得到正六棱台OO′和较小的棱锥PO′．(1)求大棱锥、小棱锥、棱台的侧面积之比；(2)若大棱锥PO的侧棱为12 cm，小棱锥底面边长为4 cm，求截得棱台的侧面积和全面积．[解]　(1)设正六棱锥的底面边长为a，侧棱长为b，则截面的边长为，∴S大棱锥侧＝c1h1＝×6a× ＝3a ，S小棱锥侧＝c2h2＝×3a× ＝a ，S棱台侧＝(c1＋c2)(h1－h2)＝(6a＋3a)× ＝a ，∴S大棱锥侧∶S小棱锥侧∶S棱台侧＝4∶1∶3．(2)S侧＝(c1＋c2)(h1－h2)＝144(cm2)，S上＝6××4×4×sin 60°＝24(cm2)，S下＝6××8×8×sin 60°＝96(cm2)，∴S全＝S侧＋S上＋S下＝144＋120(cm2)．11．水晶是一种石英结晶体矿物，因其硬度、色泽、光学性质、稀缺性等，常被人们制作成饰品．如图所示，现有棱长为2 cm的正方体水晶一块，将其裁去八个相同的四面体，打磨成某饰品，则该饰品的表面积为(单位：cm2)(　　)A．12＋4   B．16＋4C．12＋3   D．16＋3A　[由图可知，截去的是正方体八个角的三棱锥，留下一个边长为的等边三角形截面，其余6个面为边长为的正方形，所以该饰品的表面积为：6×()2＋8××()2＝12＋4，故选A．]12．(多选题)如图所示，在长方体ABCD­A1B1C1D1中，AB＝BC＝1，AA1＝2，P是A1B上的一动点，则下列选项正确的是(　　)A．DP的最小值为B．DP的最小值为C．AP＋PC1的最小值为D．AP＋PC1的最小值为AD　[求DP的最小值，即求△DA1B底边A1B上的高，易知A1B＝A1D＝，BD＝，所以A1B边上的高为h＝ ，连接A1C1，BC1(图略)，得△A1BC1，以A1B所在直线为轴，将△A1BC1所在平面旋转到平面ABB1A1，设点C1的新位置为C′，连接AC′(图略)，则AC′即为所求的最小值，易知AA1＝2，A1C′＝，cos∠AA1C′＝－，所以AC′＝＝．故选AD．]13．如图，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝2，AD＝2，则四边形ABCD绕AB所在直线旋转一周所成空间图形的表面积为________．24π＋12π　[如图所示，过点C作CE⊥AB交AB于点E，将四边形ABCD绕AB所在直线旋转一周得到的空间图形是由直角梯形ADCE旋转得到的圆台与△CBE旋转得到的圆锥拼接而成的组合体．由已知条件计算可得CE＝4，AE＝2，BE＝3，BC＝5，∴S表＝π·AD2＋π(CE＋AD)·CD＋π·CE·BC＝4π＋π·(4＋2)×2＋π×4×5＝24π＋12π．]14．一个四棱锥和一个三棱锥恰好可以拼成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等，设四棱锥，三棱锥，三棱柱的高分别为h1，h2，h，则h1∶h2∶h＝________．∶2∶2　[由题意可把三棱锥A1­ABC与四棱锥A1­BCC1B1拼成如图所示的三棱柱ABC­A1B1C1．不妨设棱长均为1，则三棱锥与三棱柱的高均为．而四棱锥A1­BCC1B1的高为，则h1∶h2∶h＝∶∶＝∶2∶2．]15．一个圆锥的底面半径为2 cm，高为6 cm，在其内部有一个高为x cm的内接圆柱．(1)求圆锥的侧面积；(2)当x为何值时，圆柱的侧面积最大？并求出侧面积的最大值．[解]　(1)圆锥的母线长为＝2(cm)，所以圆锥的侧面积S1＝π×2×2＝4π(cm2)．(2)该几何体的轴截面如图所示．设圆柱的底面半径为r cm，则＝，所以r＝．所以圆柱的侧面积S2＝2πrx＝(－x2＋6x)＝－[(x－3)2－9]＝－(x－3)2＋6π，所以当x＝3时，圆柱的侧面积取得最大值，且最大值为6π cm2．