2018年天津市北辰区中考数学二模试卷

这是一份2018年天津市北辰区中考数学二模试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2018年天津市北辰区中考数学二模试卷
一、选择题（本大题共12个小题，每小题3分，共36分）
1．（3分）计算（﹣2）+5的结果是（　　）
A．3 B．﹣3 C．7 D．﹣7
2．（3分）sin60°的值等于（　　）
A． B． C． D．
3．（3分）下面4个汉字，可以看作是轴对称图形的是（　　）
A． B． C． D．
4．（3分）某市根据主要景区统计，“五一”三天假期，全市共接待海内外游客约2588000人次，将2588000用科学记数法表示应为（　　）
A．0.2588×107 B．2.588×106 C．25.88×105 D．258.8×104
5．（3分）如图是一个由4个相同的正方体组成的立体图形，它的主视图是（　　）

A． B．.
C．. D．.
6．（3分）估计的值在（　　）
A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间
7．（3分）计算﹣的结果是（　　）
A． B． C． D．1
8．（3分）一元二次方程x2+2x﹣8＝0的两个根为（　　）
A．x1＝﹣4，x2＝2 B．x1＝﹣5，x1＝3 C．x1＝﹣2，x1＝4 D．x1＝﹣3，x1＝5
9．（3分）如图，在△ABC中，AB＝AC，∠BAC＝45°，将△ABC绕点A逆时针方向旋转得△AEF，其中，E，F是点B，C旋转后的对应点，BE，CF相交于点D．若四边形ABDF为菱形，则∠CAE的大小是（　　）

A．45° B．60° C．75° D．90°
10．（3分）已知反比例函数y＝（k为常数，k≠0）的图象经过点（﹣2，3），则当2＜x＜3时，函数值y的取值范围是（　　）
A．2＜y＜3 B．＜y＜ C．﹣6＜y＜﹣1 D．﹣3＜y＜﹣2
11．（3分）如图，在△ABC中，AB＝AC，AD，BE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于CP+EP最小值的是（　　）

A．AC B．AD C．BE D．BC
12．（3分）已知二次函数y＝ax2+bx+c（a，b，c为常数，a≠0），其中，自变量x与函数值y之间满足下面对应关系：
x
……
3
5
7
……
y＝ax2+bx+c
……
2.5
2.5
﹣1.5
……
则的值是（　　）
A．﹣6 B．6 C．﹣3 D．3
二、填空题（本大题共6小题，每小题3分，共18分）
13．（3分）计算x•x3+x4的结果等于　 　．
14．（3分）计算（+）（﹣）的结果等于　 　．
15．（3分）袋子中共装有7个球，其中3个红球，4个黄球，这些除颜色外，形状、大小、质地等完全相同，若从袋子中随机摸出1个球，则摸出的球是红球的概率是　 　．
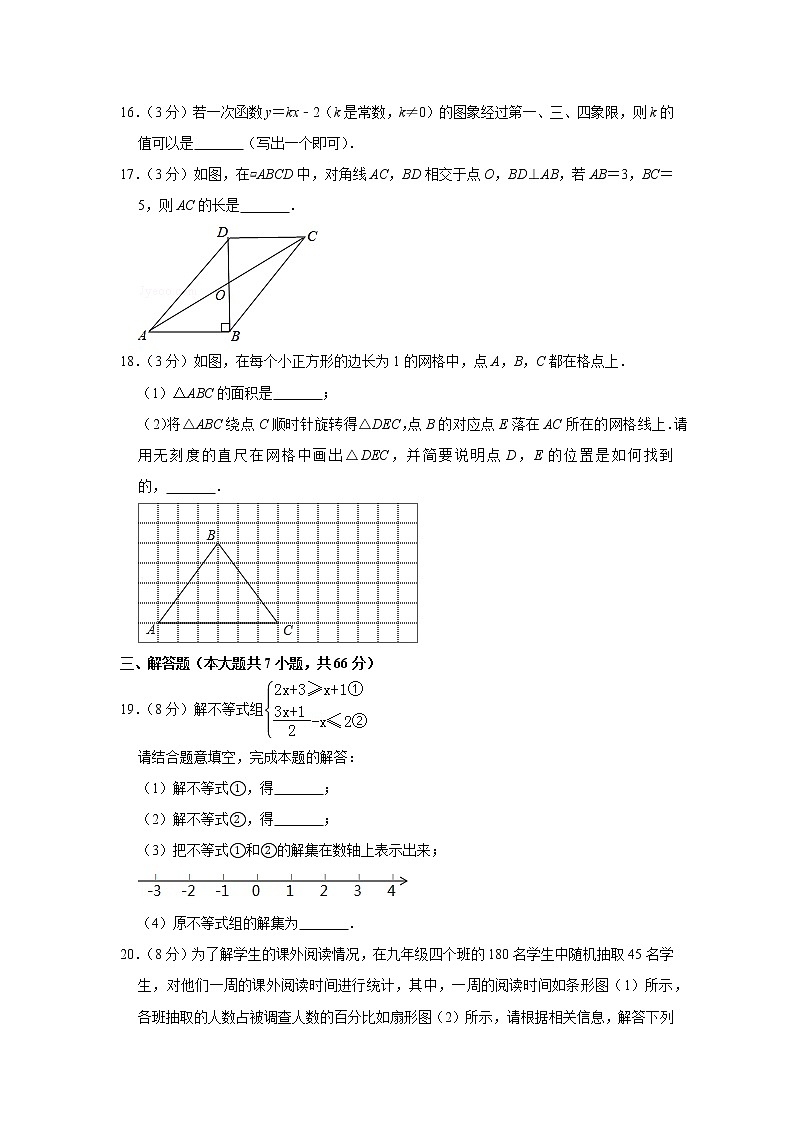
16．（3分）若一次函数y＝kx﹣2（k是常数，k≠0）的图象经过第一、三、四象限，则k的值可以是　 　（写出一个即可）．
17．（3分）如图，在▱ABCD中，对角线AC，BD相交于点O，BD⊥AB，若AB＝3，BC＝5，则AC的长是　 　．

18．（3分）如图，在每个小正方形的边长为1的网格中，点A，B，C都在格点上．
（1）△ABC的面积是　 　；
（2）将△ABC绕点C顺时针旋转得△DEC，点B的对应点E落在AC所在的网格线上．请用无刻度的直尺在网格中画出△DEC，并简要说明点D，E的位置是如何找到的，　 　．

三、解答题（本大题共7小题，共66分）
19．（8分）解不等式组
请结合题意填空，完成本题的解答：
（1）解不等式①，得　 　；
（2）解不等式②，得　 　；
（3）把不等式①和②的解集在数轴上表示出来；

（4）原不等式组的解集为　 　．
20．（8分）为了解学生的课外阅读情况，在九年级四个班的180名学生中随机抽取45名学生，对他们一周的课外阅读时间进行统计，其中，一周的阅读时间如条形图（1）所示，各班抽取的人数占被调查人数的百分比如扇形图（2）所示，请根据相关信息，解答下列问题：
（Ⅰ）随机抽取的学生中，一班的人数是　 　；
（Ⅱ）求本次调查所得样本数据的众数、中位数和平均数；
（Ⅲ）根据样本数据，估计该校九年级一周课外阅读时间大于10h的约有多少人．

21．（10分）在⊙O中，AB是⊙O直径，AC是弦，∠BAC＝50°．
（Ⅰ）如图（1），D是AB上一点，AD＝AC，延长CD交⊙O于点E，求∠CEO的大小；
（Ⅱ）如图（2），D是AC延长线上一点，AD＝AB，连接BD交⊙O于点E，求∠CEO的大小．

22．（10分）如图，测量建筑物CE的高度和顶部避雷针CD的高度，在A处测得避雷针顶部D的仰角为45°，建筑物顶部C的仰角为35°，在B处测得C的仰角为58°，已知测点A、B与楼底E在同一条直线上，AB＝18m，求建筑物CE和避雷针CD的高度（结果保留一位小数）．结果保留数据：tan35°≈0.70，tan58°≈1.60．

23．（10分）已知甲、乙两种商品的进价和售价如表所示：

甲
乙
进价（元/价）
15
35
售价（元/价）
20
45
（Ⅰ）商场购进甲、乙两种商品共180件，两种商品很快销售完，并获得利润1300元，求商场甲、乙两种商品各购进了多少件？（利润＝售价﹣进价）
（Ⅱ）商场计划再次购进甲、乙两种商品共180件．设计划购进甲商品x件，计划销售完本次两种商品共获得利润y元．
①列出y与x之间的函数关系式；
②若商场计划购进的乙商品数不超过甲商品数的2倍，求当x取何值时，可使商场本次计划销售所获得的利润最大？
24．（10分）在平面直角坐标系中，点A（﹣2，0），B（2，0），C（0，2），点D、E分别是AC，BC的中点，将△CDE绕点C逆时针旋转得△CMN，点M，N分别是点D，E旋转后的对应点，记旋转角α．

（Ⅰ）如图1，求证AM＝BN；
（Ⅱ）如图2，当α＝75°时，求点N的坐标；
（Ⅲ）当AM∥CN，求BN的长（直接写出结果即可）．
25．（10分）抛物线y＝x2+bx+c（b，c为常数）与y轴相交于点C，经过点C作直线CD∥x轴，交抛物线于点D，将直线CD向上平移t个单位长度，交抛物线于点A和B（A在B的左侧），直线AB与抛物线的对称轴l交于点E．
（Ⅰ）当b＝﹣2，c＝1时，求抛物线顶点P的坐标；
（Ⅱ）若∠ACB＝90°，求t的值；
（Ⅲ）在（2）的条件下，当以点A，D，C，E为顶点的四边形为平行四边形时，求b的值．

2018年天津市北辰区中考数学二模试卷
参考答案与试题解析
一、选择题（本大题共12个小题，每小题3分，共36分）
1．（3分）计算（﹣2）+5的结果是（　　）
A．3 B．﹣3 C．7 D．﹣7
【分析】根据异号两数相加，取绝对值较大的加数的符号，再用较大的绝对值减去较小的绝对值．
【解答】解：原式＝（5﹣2）＝3，
故选：A．
【点评】本题考查了有理数的加法，异号两数相加，取绝对值较大的加数的符号，再用较大的绝对值减去较小的绝对值，注意和的符号．
2．（3分）sin60°的值等于（　　）
A． B． C． D．
【分析】直接利用特殊角的三角函数值求出答案．
【解答】解：sin60°＝．
故选：C．
【点评】此题主要考查了特殊角的三角函数值，正确把握定义是解题关键．
3．（3分）下面4个汉字，可以看作是轴对称图形的是（　　）
A． B． C． D．
【分析】根据轴对称图形的概念判断即可．
【解答】解：A、不是轴对称图形；
B、不是轴对称图形；
C、不是轴对称图形；
D、是轴对称图形；
故选：D．
【点评】本题考查的是轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
4．（3分）某市根据主要景区统计，“五一”三天假期，全市共接待海内外游客约2588000人次，将2588000用科学记数法表示应为（　　）
A．0.2588×107 B．2.588×106 C．25.88×105 D．258.8×104
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：2588000＝2.588×106，
故选：B．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
5．（3分）如图是一个由4个相同的正方体组成的立体图形，它的主视图是（　　）

A． B．.
C．. D．.
【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．
【解答】解：该立体图形主视图的第1列有1个正方形、第2列有1个正方形、第3列有2个正方形，
故选：C．
【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．
6．（3分）估计的值在（　　）
A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间
【分析】估算确定出所求数的范围即可．
【解答】解：∵25＜29＜36，
∴5＜＜6，即5和6之间，
故选：C．
【点评】此题考查了估算无理数的大小，以及算术平方根，熟练掌握估算的方法是解本题的关键．
7．（3分）计算﹣的结果是（　　）
A． B． C． D．1
【分析】直接利用分式加减运算法则计算得出答案．
【解答】解：﹣＝＝1．
故选：D．
【点评】此题主要考查了分式的加减运算，正确掌握运算法则是解题关键．
8．（3分）一元二次方程x2+2x﹣8＝0的两个根为（　　）
A．x1＝﹣4，x2＝2 B．x1＝﹣5，x1＝3 C．x1＝﹣2，x1＝4 D．x1＝﹣3，x1＝5
【分析】利用因式分解法解方程即可得到正确选项．
【解答】解：（x+4）（x﹣2）＝0，
x+4＝0或x﹣2＝0，
所以x1＝﹣4，x2＝2．
故选：A．
【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
9．（3分）如图，在△ABC中，AB＝AC，∠BAC＝45°，将△ABC绕点A逆时针方向旋转得△AEF，其中，E，F是点B，C旋转后的对应点，BE，CF相交于点D．若四边形ABDF为菱形，则∠CAE的大小是（　　）

A．45° B．60° C．75° D．90°
【分析】由题意可得AB∥CF，可得∠ACF＝45°，根据AB＝AC＝AF，可得∠AFC＝45°即∠CAF＝90°且∠EAF＝45°则可求∠CAE的大小．
【解答】解：∵ABDF是菱形
∴AB∥CF，AB＝AF
∴∠BAC＝∠ACF＝45°，AF＝AC
∴∠ACF＝∠AFC＝45°
∴∠CAF＝90°
∵将△ABC绕点A逆时针方向旋转得△AEF
∴∠EAF＝∠BAC＝45°
∴∠EAC＝∠CAF﹣∠EAF＝45°
故选：A．
【点评】本题考查了旋转的性质，菱形的性质，等腰三角形的性质，关键是灵活运用这些性质解决问题．
10．（3分）已知反比例函数y＝（k为常数，k≠0）的图象经过点（﹣2，3），则当2＜x＜3时，函数值y的取值范围是（　　）
A．2＜y＜3 B．＜y＜ C．﹣6＜y＜﹣1 D．﹣3＜y＜﹣2
【分析】先把（﹣2，3）代入y＝中求出k得到反比例函数解析式为y＝﹣，再分别计算出自变量为2和3对应的反比例函数值，然后根据反比例函数的性质求解．
【解答】解：把（﹣2，3）代入y＝得k＝﹣2×3＝6，
所以反比例函数解析式为y＝﹣，
当x＝2时，y＝﹣＝﹣3；当x＝3时，y＝﹣＝﹣2；
所以当2＜x＜3时，函数值y的取值范围为﹣3＜y＜﹣2．
故选：D．
【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数y＝（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy＝k．
11．（3分）如图，在△ABC中，AB＝AC，AD，BE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于CP+EP最小值的是（　　）

A．AC B．AD C．BE D．BC
【分析】如图连接PB，只要证明PB＝PC，即可推出PC+PE＝PB+PE，由PE+PB≥BE，可得P、B、E共线时，PB+PE的值最小，最小值为BE的长度．
【解答】解：如图，连接PB，
∵AB＝AC，BD＝CD，
∴AD⊥BC，
∴PB＝PC，
∴PC+PE＝PB+PE，
∵PE+PB≥BE，
∴P、B、E共线时，PB+PE的值最小，最小值为BE的长度，
故选：C．

【点评】本题考查轴对称﹣最短路线问题，等腰三角形的性质、线段的垂直平分线的性质等知识，解题的关键是灵活运用所学知识解决问题．
12．（3分）已知二次函数y＝ax2+bx+c（a，b，c为常数，a≠0），其中，自变量x与函数值y之间满足下面对应关系：
x
……
3
5
7
……
y＝ax2+bx+c
……
2.5
2.5
﹣1.5
……
则的值是（　　）
A．﹣6 B．6 C．﹣3 D．3
【分析】利用待定系数法求出二次函数解析式，计算即可》
【解答】解：由题意得，，
解得，，
则＝6，
故选：B．
【点评】本题考查的是二次函数图象上点的坐标特征、待定系数法求二次函数解析式，掌握待定系数法求二次函数解析式的一般步骤是解题的关键．
二、填空题（本大题共6小题，每小题3分，共18分）
13．（3分）计算x•x3+x4的结果等于　2x4　．
【分析】根据同底数幂的乘法，即可解答．
【解答】解：x•x3+x4＝2x4，
故答案为：2x4
【点评】此题考查同底数幂的乘法，关键是根据法则计算．
14．（3分）计算（+）（﹣）的结果等于　8　．
【分析】利用平方差公式计算．
【解答】解：原式＝10﹣2
＝8．
故答案为8．
【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
15．（3分）袋子中共装有7个球，其中3个红球，4个黄球，这些除颜色外，形状、大小、质地等完全相同，若从袋子中随机摸出1个球，则摸出的球是红球的概率是　　．
【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．
【解答】解：∵袋子中共有7个小球，其中红球有3个，
∴摸出的球是红球的概率是，
故答案为：．
【点评】此题主要考查了概率的求法，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．
16．（3分）若一次函数y＝kx﹣2（k是常数，k≠0）的图象经过第一、三、四象限，则k的值可以是　2　（写出一个即可）．
【分析】由一次函数图象经过第一、三、四象限，可知k＞0，﹣2＜0，在范围内确定k的值即可．
【解答】解：因为一次函数y＝kx﹣2（k是常数，k≠0）的图象经过第一、三、四象限，
所以k＞0，﹣2＜0，
所以k可以取2，
故答案为：2
【点评】此题考查一次函数图象与系数的关系，根据一次函数图象所经过的象限，可确定一次项系数，常数项的值的符号，从而确定字母k的取值范围．
17．（3分）如图，在▱ABCD中，对角线AC，BD相交于点O，BD⊥AB，若AB＝3，BC＝5，则AC的长是　2　．

【分析】直接构造直角三角形，再利用平行四边形的性质结合勾股定理得出AC的长．
【解答】解：延长AB，过点C作CE⊥AB交于点E，
∵四边形ABCD是平行四边形，
∴AB＝DC＝3，BC＝AD＝5，DC∥AB，
∵BD⊥AB，AB＝3，BC＝5，
∴BD＝4，
∵DC∥AB，∠ABD＝90°，
∴∠CDB＝90°，
可得：∠CDB＝∠DBC＝∠BEC＝90°，
则四边形DBEC是矩形，
故DB＝EC＝4，DC＝BE＝3，
∴AE＝6，
∴AC＝＝2．
故答案为：2．

【点评】此题主要考查了勾股定理以及平行四边形的性质，正确作出辅助线是解题关键．
18．（3分）如图，在每个小正方形的边长为1的网格中，点A，B，C都在格点上．
（1）△ABC的面积是　12　；
（2）将△ABC绕点C顺时针旋转得△DEC，点B的对应点E落在AC所在的网格线上．请用无刻度的直尺在网格中画出△DEC，并简要说明点D，E的位置是如何找到的，　先取格点E、F、M、N，连接MN，再延长CF交MN于D，则△DEC为所作　．

【分析】（1）直接利用三角形面积公式计算；
（2）先取格点E、F、M、N，使CE＝CF＝CB，CN＝6，D点为MN与CF的交点，则△CEF为等腰三角形，利用MN∥EF得到△CND为等腰三角形，则CD＝CN＝6，从而得到满足条件的△CDE．
【解答】解：（1）△ABC的面积＝×6×4＝12；
（2）如图，先取格点E、F、M、N，连接MN，再延长CF交MN于D，则△DEC为所作．

故答案为12，先取格点E、F、M、N，连接MN，再延长CF交MN于D，则△DEC为所作．
【点评】本题考查了作图﹣旋转图形：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
三、解答题（本大题共7小题，共66分）
19．（8分）解不等式组
请结合题意填空，完成本题的解答：
（1）解不等式①，得　x≥﹣2　；
（2）解不等式②，得　x≤3　；
（3）把不等式①和②的解集在数轴上表示出来；

（4）原不等式组的解集为　﹣2≤x≤3　．
【分析】分别解两个不等式，然后根据公共部分确定不等式组的解集，再利用数轴表示解集；
【解答】解：解不等式①得x≥﹣2，
解不等式②得x≤3，
所以不等式组的解集为﹣2≤x≤3，
用数轴表示为：，
故答案为：x≥﹣2；x≤3；﹣2≤x≤3．
【点评】本题考查了解一元一次不等式组：一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
20．（8分）为了解学生的课外阅读情况，在九年级四个班的180名学生中随机抽取45名学生，对他们一周的课外阅读时间进行统计，其中，一周的阅读时间如条形图（1）所示，各班抽取的人数占被调查人数的百分比如扇形图（2）所示，请根据相关信息，解答下列问题：
（Ⅰ）随机抽取的学生中，一班的人数是　18　；
（Ⅱ）求本次调查所得样本数据的众数、中位数和平均数；
（Ⅲ）根据样本数据，估计该校九年级一周课外阅读时间大于10h的约有多少人．

【分析】（Ⅰ）由百分比之和为1求得一班百分比，再用总人数乘以所得百分比即可得；
（Ⅱ）根据众数、中位数和平均数的定义求解；
（Ⅲ）用总人数乘以样本中阅读时间大于10h的人所占比例即可得．
【解答】解：（Ⅰ）∵一班人数所占比例为1﹣（20%+20%+20%）＝40%，
∴一班人数为45×40%＝18人，
故答案为：18；

（Ⅱ）∵9出现了15次，次数最多，
∴众数为9；
∵共有45个数据，其中位数是第23个数据，
∴中位数是10，
平均数为＝10；

（Ⅲ）估计该校九年级一周课外阅读时间大于10h的约有180×＝60人．
【点评】本题考查的是扇形统计图与条形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．
21．（10分）在⊙O中，AB是⊙O直径，AC是弦，∠BAC＝50°．
（Ⅰ）如图（1），D是AB上一点，AD＝AC，延长CD交⊙O于点E，求∠CEO的大小；
（Ⅱ）如图（2），D是AC延长线上一点，AD＝AB，连接BD交⊙O于点E，求∠CEO的大小．

【分析】（Ⅰ）由已知AD＝AC，∠A＝50°，可求得∠C＝∠ADC＝65°，由圆心角、圆周角间关系，可得∠AOE的度数，利用三角形的外角内角关系，可求得∠CEO的度数．
（Ⅱ）由已知AD＝AC，∠A＝50°，可求得∠D＝∠B＝65°，由四边形ABEC是圆内接四边形，可得∠CEB的度数，利用角的和差⊊关系，可求得∠CEO的度数．
【解答】解：（Ⅰ）∵AD＝AC，∠A＝50°，
∴∠C＝∠ADC＝65°，
∴∠ADE＝180°﹣∠ADC
＝180°﹣65°
＝115°
∵∠AOE＝2∠C＝130°，
∴∠CEO＝∠AOE﹣∠ADE
＝130°﹣115°
＝15°
（Ⅱ）∵AD＝AB，∠A＝50°
∴∠D＝∠B＝65°，
∵OB＝OE，
∴∠OEB＝∠B＝65°，
∵四边形ABEC是圆内接四边形，
∴∠BEC＝180°﹣∠A＝130°
∴∠CEO＝∠CEB﹣∠OEB
＝130°﹣65°
＝65°


【点评】本题考查了圆周角定理、圆内接四边形的性质、等腰三角形的性质等知识点，难度中等．圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
22．（10分）如图，测量建筑物CE的高度和顶部避雷针CD的高度，在A处测得避雷针顶部D的仰角为45°，建筑物顶部C的仰角为35°，在B处测得C的仰角为58°，已知测点A、B与楼底E在同一条直线上，AB＝18m，求建筑物CE和避雷针CD的高度（结果保留一位小数）．结果保留数据：tan35°≈0.70，tan58°≈1.60．

【分析】根据直角三角形的性质好三角函数解答即可．
【解答】解：根据题意，有AB＝18，∠DAE＝45°，∠CAE＝35°，∠CBE＝58°，
在Rt△CAE中，tan∠CAE＝，
∴CE＝AE•tan∠CAE＝AE•tan35°，
在Rt△CBE中，tan∠CBE＝，
∴CE＝BE•tan∠CBE═BE•tan58°，
∴AE•tan35°＝BE•tan58°，
设BE＝x，则有（18+x）×0.70＝x×1.60，
解得：x≈14.0，
即BE≈14.0，
∴CE＝BE•tan58°≈14.0×1.60≈22.4，
AE＝AB+BE≈18+14.0≈32.0，
在Rt△ADE中，∠DAE＝45°，
∴DE＝AE≈32.0，
∴CD＝DE﹣CE≈32.0﹣22.4＝9.6，
答：建筑物CE的高度约为22.4米，避雷针CD的高度约为9.6米．
【点评】此题综合考查了仰角、坡度的定义，能够正确地构建出直角三角形，将实际问题化归为解直角三角形的问题是解答此类题的关键．
23．（10分）已知甲、乙两种商品的进价和售价如表所示：

甲
乙
进价（元/价）
15
35
售价（元/价）
20
45
（Ⅰ）商场购进甲、乙两种商品共180件，两种商品很快销售完，并获得利润1300元，求商场甲、乙两种商品各购进了多少件？（利润＝售价﹣进价）
（Ⅱ）商场计划再次购进甲、乙两种商品共180件．设计划购进甲商品x件，计划销售完本次两种商品共获得利润y元．
①列出y与x之间的函数关系式；
②若商场计划购进的乙商品数不超过甲商品数的2倍，求当x取何值时，可使商场本次计划销售所获得的利润最大？
【分析】（Ⅰ）首先设出未知数，根据题意可得两个等量关系：①甲、乙两种商品共180件；②获得利润1300元；依此列出方程组，解方程组即可；
（Ⅱ）①根据总利润＝甲种商品利润+乙种商品利润即可解决问题；
②根据商场计划购进的乙商品数不超过甲商品数的2倍列出不等式，求出x的取值范围，然后根据一次函数的增减性解决最大值问题．
【解答】解：（Ⅰ）设商场购进甲商品x件，乙商品y件．
根据题意，得，
解得．
答：商场购进甲商品100件，乙商品80件；

（Ⅱ）①设计划购进甲商品x件，
由题意，可得y＝5x+10（180﹣x）＝﹣5x+1800（0≤x≤180）．

②设计划购进甲种商品x件，
由题意，可得180﹣x≤2x，解得x≥60．
∵0≤x≤180，
∴60≤x≤180．
又∵y＝﹣5x+1800，
∴k＝﹣5＜0，
∴y随x增大而减小，
∴x＝60时，y的值最大，最大值是1500．
【点评】本题考查二元一次方程组的应用、一次函数的应用、一元一次不等式的应用，解题的关键是理解题意，学会利用一次函数的性质解决实际问题中的最值问题，属于中考常考题型．
24．（10分）在平面直角坐标系中，点A（﹣2，0），B（2，0），C（0，2），点D、E分别是AC，BC的中点，将△CDE绕点C逆时针旋转得△CMN，点M，N分别是点D，E旋转后的对应点，记旋转角α．

（Ⅰ）如图1，求证AM＝BN；
（Ⅱ）如图2，当α＝75°时，求点N的坐标；
（Ⅲ）当AM∥CN，求BN的长（直接写出结果即可）．
【分析】（1）根据点的坐标可以发现OA＝OB＝OC，可得AC＝BC．通过旋转性质可得CM＝CN，∠ACM＝∠BCN．由此可以证明△ACM≌△BCN可得AM＝BN
（2）作NQ⊥y轴，由勾股定理可得BC＝2，可得CE＝CN＝，因为旋转角为75°且∠OCB＝45°，所以∠NCQ＝60°，可以根据勾股定理求出NQ，CQ的长度，即可得N点坐标
（3）因为AM∥CN，所以∠MCN＝∠AMC＝90°，再根据勾股定理得AM的长度，由AM＝BN可得BN的长度
【解答】（1）证明：∵A（﹣2，0），B（2，0），C（0，2）
∴OA＝OB＝OC 且∠AOC＝∠BOC
∴△AOC≌△BOC
∴AC＝BC

∵D，E分别是AC，BC的中点
∴DC＝CE
∵△MCN是△DCE旋转得到的
∴∠ACM＝∠BCN，CM＝CD，CE＝CN
∴CM＝CN且∠ACM＝∠BCN，AC＝BC
∴△ACM≌△BCN
∴AM＝BN
（2）如图2．∵∠BCO＝45°，∠BCN＝∠α＝75°
∴∠OCN＝120°

过点作NQ⊥y轴，Q为垂足．
∴∠NCQ＝60°
在Rt△BCO中，BC＝
∴CE＝CN＝
在Rt△NCQ中，∠NCQ＝60°∴∠QNC＝30°
∴CQ＝CN＝，NQ＝CQ＝
∴OQ＝CO+CQ＝
∴
（3）如图3

当AM∥CN 时，∴∠MCN＝∠AMC＝90°
在Rt△ACM中，AC＝2，CM＝∴
AM＝
∵AM＝BN
∴BN＝
【点评】本题考查全等三角形的证明，旋转的性质，以及利用勾股定理求直角三角形的边长．
25．（10分）抛物线y＝x2+bx+c（b，c为常数）与y轴相交于点C，经过点C作直线CD∥x轴，交抛物线于点D，将直线CD向上平移t个单位长度，交抛物线于点A和B（A在B的左侧），直线AB与抛物线的对称轴l交于点E．
（Ⅰ）当b＝﹣2，c＝1时，求抛物线顶点P的坐标；
（Ⅱ）若∠ACB＝90°，求t的值；
（Ⅲ）在（2）的条件下，当以点A，D，C，E为顶点的四边形为平行四边形时，求b的值．
【分析】（Ⅰ）把b＝﹣2，c＝1代入抛物线的解析式，利用配方法求出顶点坐标即可；
（Ⅱ）当∠ACB＝90°，根据AE＝CE，构建方程即可解决问题；
（Ⅲ）根据AE＝CD，构建方程即可解决问题；
【解答】解：（Ⅰ）把b＝﹣2，c＝1代入y＝x2+bx+c，
得到y＝x2﹣2x+1＝（x﹣2）2﹣1，
∴抛物线的顶点P的坐标为（2，﹣1）．

（Ⅱ）如图，

∵∠ACB＝90°，AE＝EB，
∴CE＝AB，
由x2+bx+c＝c+t，解得x＝﹣b±，
∴A（﹣b﹣，c+t），B（﹣b+，c+t），
∴AB＝2，
∵E（﹣b，c+t），C（0，c），
∴CE＝
∴＝，
解得t＝2或0（舍弃），
∴t＝2．

（Ⅲ）由题意CD＝AE，
∵A（﹣b﹣，c+t），E（﹣b，c+t），且点A中点E的左侧，
∴AE＝，
∵C（0，c），D（﹣2b，c），
∴CD＝|﹣2b|，
∴＝|﹣2b|，
∴3b2＝2t，
∵t＝2，
∴b＝±．
【点评】本题考查二次函数综合题、直角三角形斜边中线的性质、平行四边形的性质等知识，解题的关键是学会利用参数，构建方程解决问题，属于中考压轴题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/5/9 9:43:49；用户：15268102978；邮箱：15268102978；学号：24559962