天津外国语大学附属外国语学校（小外）2018-2019年度初三上第一次月考数学试卷（含解析）

这是一份天津外国语大学附属外国语学校（小外）2018-2019年度初三上第一次月考数学试卷（含解析），共18页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

天津外国语大学附属外国语学校（小外）2018-2019年度初三
第一次月考数学试卷
一、选择题（3×10＝30）
1．下面图形中，是中心对称图形的是（　　）
A． B．
C． D．
2．已知0≤x≤，那么函数y＝﹣2x2+8x﹣6的最大值是（　　）
A．﹣10.5 B．2 C．﹣2.5 D．﹣6
3．在平面直角坐标系中，将抛物线y＝x2+2x+3绕着原点旋转180°，所得抛物线的解析式是（　　）
A．y＝﹣（x﹣1）2﹣2 B．y＝﹣（x+1）2﹣2
C．y＝﹣（x﹣1）2+2 D．y＝﹣（x+1）2+2
4．已知二次函数y＝3（x﹣1）2+k的图象上有三点A（，y1），B（2，y2），C（﹣，y3），则y1、y2、y3的大小关系为（　　）
A．y1＞y2＞y3 B．y2＞y1＞y3 C．y3＞y1＞y2 D．y3＞y2＞y1
5．在同一平面直角坐标系中，函数y＝mx+n与y＝mx2﹣nx的图象可能是（　　）
A． B．
C． D．
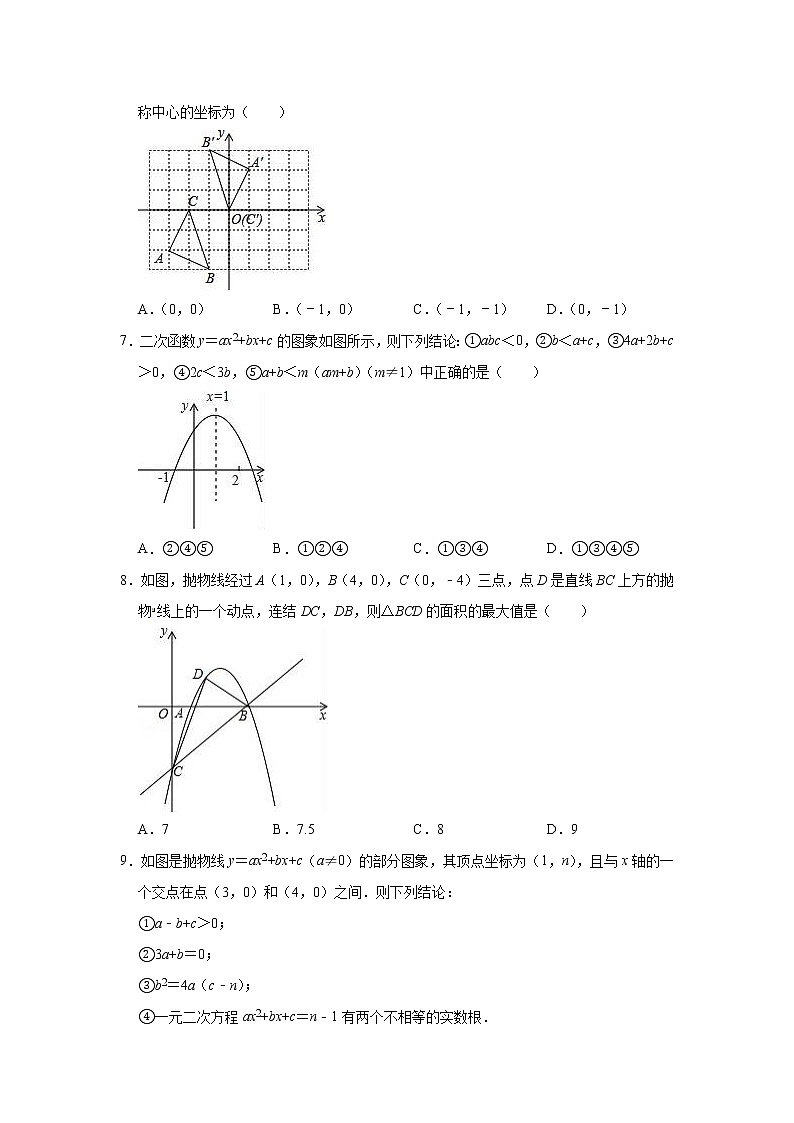
6．如图，在平面直角坐标系xOy中，△ABC经过中心对称变换得到△A′B′C′，那么对称中心的坐标为（　　）

A．（0，0） B．（﹣1，0） C．（﹣1，﹣1） D．（0，﹣1）
7．二次函数y＝ax2+bx+c的图象如图所示，则下列结论：①abc＜0，②b＜a+c，③4a+2b+c＞0，④2c＜3b，⑤a+b＜m（am+b）（m≠1）中正确的是（　　）

A．②④⑤ B．①②④ C．①③④ D．①③④⑤
8．如图，抛物线经过A（1，0），B（4，0），C（0，﹣4）三点，点D是直线BC上方的抛物线上的一个动点，连结DC，DB，则△BCD的面积的最大值是（　　）

A．7 B．7.5 C．8 D．9
9．如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：
①a﹣b+c＞0；
②3a+b＝0；
③b2＝4a（c﹣n）；
④一元二次方程ax2+bx+c＝n﹣1有两个不相等的实数根．
其中正确结论的个数是（　　）

A．1 B．2 C．3 D．4
10．如图，正方形ABCD的边长为4，点M是CD的中点，动点E从点B出发，沿BC运动，到点C时停止运动，速度为每秒1个长度单位；动点F从点M出发，沿M→D→A远动，速度也为每秒1个长度单位：动点G从点D出发，沿DA运动，速度为每秒2个长度单位，到点A后沿AD返回，返回时速度为每秒1个长度单位，三个点的运动同时开始，同时结束．设点E的运动时间为x，△EFG的面积为y，下列能表示y与x的函数关系的图象是（　　）

A． B．
C． D．
二、填空题：（4x8＝32）
11．已知二次函数y＝x2+（2m﹣1）x，当﹣2＜x＜0时，y随x的增大而减小，则m的取值范围是　 　．
12．若函数y＝mx2+（m+2）x+m+1的图象与x轴只有一个交点，那么m的值为　 　．
13．二次函数y＝ax2+bx+c图象上部分点的坐标满足如表：
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
若关于x的一元二次方程ax2+bx+c﹣m＝0有两个不相等的实数根，则m的取值范围是　 　．
14．当0≤x≤1时，二次函数y＝x2+ax﹣+有最大值2，则a的值为　 　．
15．如图，平行于x轴的直线AC分别交抛物线y1＝x2（x≥0）与y2＝（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则＝　 　．

16．二次函数y＝x2+bx的图象如图，对称轴为直线x＝1．若关于x的一元二次方程x2+bx﹣t＝0（t为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是　 　．

17．如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA＝6，PB＝8，PC＝10，则四边形APBQ的面积为　 　．

18．小刚家、公交车站、学校在一条笔直的公路旁（小刚家、学校到这条公路的距离忽略不计）．一天，小刚从家出发去上学，沿这条公路步行到公交站恰好乘上一辆公交车，公交车沿这条公路匀速行驶，小刚下车时发现还有4分钟上课，于是他沿着这条公路跑步赶到学校（上、下车时间忽略不计），小刚与学校的距离s（单位：米）与他所用的时间t（单位：分钟）之间的函数关系如图所示．已知小刚从家出发7分钟时与家的距离是1200米，从上公交车到他到达学校共用10分钟．下列说法：
①公交车的速度为400米/分钟；
②小刚从家出发5分钟时乘上公交车；
③小刚下公交车后跑向学校的速度是100米/分钟；
④小刚上课迟到了1分钟．
其中正确的序号是　 　．

三.解答题
19．（9分）已知关于x的方程x2﹣2（k﹣1）x+k2＝0有两个实数根x1，x2．
（1）求k的取值范围；
（2）若|x1+x2|＝x1x2﹣1，求k的值．
20．（9分）如图，抛物线y＝ax2+bx+c经过点A（﹣3，0），B（1，0），C（0，﹣3）
（1）求抛物线的解析式；
（2）若点P为抛物线对称轴上一点，求△PBC周长取得最小值时点P的坐标；
（3）设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M使得ADM是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．

21．（10分）已知天津市某水产养殖户进行小龙新养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价P（元/千克）与时间t（t为整数）的函数关系为日销量y是时间第t天的一次函数，通过调查发现第1天的销量是198千克，第80天的销量是40千克．
（1）求日销量y与时间t的函数解析式；
（2）哪一天的日销售利润最大？最大利润是多少？
（3）该养殖户有多少天利润不低于2400元．
22．（10分）抛物线y＝x2+bx+c的图象经过点A（﹣1，0），B（0，﹣3）．

（Ⅰ）求这个抛物线的解析式；
（Ⅱ）抛物线与x轴的另一交点为C，抛物线的顶点为D，判断△CBD的形状；
（Ⅲ）直线BN∥x轴，交抛物线于另一点N，点P是直线BN下方的抛物线上的一个动点（点P不与点B和点N重合），过点P作x轴的垂线，交直线BC于点Q，当四边形BPNQ的面积最大时，求出点P的坐标．

参考答案
一、选择题
1．解：A、不是中心对称图形，本选项错误；
B、是中心对称图形，本选项正确；
C、不是中心对称图形，本选项错误；
D、不是中心对称图形，本选项错误．
故选：B．
2．解：∵y＝﹣2x2+8x﹣6＝﹣2（x﹣2）2+2．
∴该抛物线的对称轴是x＝2，且在x＜2上y随x的增大而增大．
又∵0≤x≤，
∴当x＝时，y取最大值，y最大＝﹣2（﹣2）2+2＝﹣2.5．
故选：C．
3．解：y＝x2+2x+3＝（x+1）2+2，抛物线y＝x2+2x+3的顶点坐标为（﹣1，2），点（﹣1，2）关于原点的对称点为（1，﹣2），
所以抛物线y＝x2+2x+3绕着原点旋转180°，所得抛物线的解析式是y＝﹣（x﹣1）2﹣2．
故选：A．
4．解：A（，y1），B（2，y2）在对称轴的右侧，y随x的增大而增大，
因为＜2，故y1＜y2，
根据二次函数图象的对称性可知，C（﹣，y3）中，|﹣﹣1|＞|2﹣1|，故有y3＞y2；
于是y3＞y2＞y1．
故选：D．
5．解：若函数y＝mx+n经过一二三象限，m＞0，n＞0，则二次函数y＝mx2﹣nx的图象开口向上，对称轴x＝﹣＞0，在y轴的右侧；
若函数y＝mx+n经过一二四象限，m＜0，n＞0，则二次函数y＝mx2﹣nx的图象开口向下，对称轴x＝﹣＜0，在y轴的左侧；
故选：C．
6．解：由图可知，点A与点A'关于（﹣1，0）对称，点B与点B'关于（﹣1，0）对称，点C与点C′关于（﹣1，0）对称，
所以△ABC与△A′B′C′关于点（﹣1，0）成中心对称，
故选：B．
7．解：①由图象可知：a＜0，b＞0，c＞0，abc＜0，故此选项正确；
②当x＝﹣1时，y＝a﹣b+c＜0，即b＞a+c，错误；
③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，故此选项正确；
④当x＝3时函数值小于0，y＝9a+3b+c＜0，且x＝﹣＝1，
即a＝﹣b，代入得9（﹣b）+3b+c＜0，得2c＜3b，故此选项正确；
⑤当x＝1时，y的值最大．此时，y＝a+b+c，
而当x＝m时，y＝am2+bm+c，
所以a+b+c＞am2+bm+c，
故a+b＞am2+bm，即a+b＞m（am+b），故此选项错误．
故①③④正确．
故选：C．
8．解：设抛物线的解析式是y＝ax2+bx+c，
∵抛物线经过A（1，0），B（4，0），C（0，﹣4）三点，
∴
解得，
∴y＝﹣x2+5x﹣4，
设过点B（4，0），C（0，﹣4）的直线的解析式为y＝kx+m

解得，
即直线BC的直线解析式为：y＝x﹣4，
设点D的坐标是（x，﹣x2+5x﹣4）
∴＝﹣2（x﹣2）2+8，
∴当x＝2时，△BCD的面积取得最大值，最大值是8．
故选：C．
9．解：∵抛物线与x轴的一个交点在点（3，0）和（4，0）之间，而抛物线的对称轴为直线x＝1，
∴抛物线与x轴的另一个交点在点（﹣2，0）和（﹣1，0）之间．
∴当x＝﹣1时，y＞0，
即a﹣b+c＞0，所以①正确；
∵抛物线的对称轴为直线x＝﹣＝1，即b＝﹣2a，
∴3a+b＝3a﹣2a＝a，所以②错误；
∵抛物线的顶点坐标为（1，n），
∴＝n，
∴b2＝4ac﹣4an＝4a（c﹣n），所以③正确；
∵抛物线与直线y＝n有一个公共点，
∴抛物线与直线y＝n﹣1有2个公共点，
∴一元二次方程ax2+bx+c＝n﹣1有两个不相等的实数根，所以④正确．
故选：C．
10．解：（1）当x≤2时，各点位置与原图所示，
此时，BE＝x，MF＝x，GD＝2x，
则y＝S△EFG＝S正方形ABCD﹣S梯形ABGE﹣S△EFC﹣S△GFD，
将有关数据代入整理得：y＝S△EFG＝1.5x2﹣x+4，对应图象是二次函数；
（2）当x＞2时，各点位置与下图所示，

此时y＝S△EFG＝•GF•AB＝﹣4x+16，对应图象是直线，
故选：A．
二、填空题：（4x8＝32）
11．解：二次函数y＝x2+（2m﹣1）x的对称轴是直线x＝﹣＝﹣，
∵二次函数y＝x2+（2m﹣1）x中a＝1＞0，
∴函数的图象的开口向上，
∴当x时，y随x的增大而减小，
∵当﹣2＜x＜0时，y随x的增大而减小，
∴﹣≥0，
解得：m，
故答案为：m．
12．解：当m＝0时，函数为y＝2x+1，其图象与x轴只有一个交点．
当m≠0时，△＝0，即（m+2）2﹣4m（）＝0．
解得：m＝±2．
∴当m＝0，或m＝±2时，函数y＝mx2+（m+2）x+m+1的图象与x轴只有一个交点．
故答案为：0或2或﹣2．
13．解：∵x＝﹣3和x＝﹣1时，y＝﹣3，
∴抛物线的对称轴为直线x＝﹣2，抛物线的顶点坐标为（﹣2，﹣2），抛物线开口向上，
∴抛物线有最小值为﹣2，
即一元二次方程ax2+bx+c＝﹣2有两个相等的实数根，
∵关于x的一元二次方程ax2+bx+c＝m有两个不相等的实数根，
∴m＞﹣2．
故答案为m＞﹣2．
14．解：∵二次函数y＝x2+ax﹣+＝（x+）2﹣﹣+，当0≤x≤1时，二次函数y＝x2+ax﹣+有最大值2，
∴当＞1时，得a＜﹣2，在0≤x≤1中，当x＝0时，该函数取得最大值，即﹣+＝2，得a＝﹣6，
当＜0时，得a＞0，在0≤x≤1中，当x＝1时，该函数取得最大值，即1+a﹣+＝2，得a＝，
由上可得，a的值是﹣6或，
故答案为：﹣6或．
15．解：设A点坐标为（0，a），（a＞0），
则x2＝a，解得x＝，
∴点B（，a），＝a，
则x＝，
∴点C（，a），
∴BC＝﹣．
∵CD∥y轴，
∴点D的横坐标与点C的横坐标相同，为，
∴y1＝（）2＝5a，
∴点D的坐标为（，5a）．
∵DE∥AC，
∴点E的纵坐标为5a，
∴＝5a，
∴x＝5，
∴点E的坐标为（5，5a），
∴DE＝5﹣，
∴＝＝5﹣．
故答案是：5﹣．
16．解：∵对称轴为直线x＝﹣＝1，
∴b＝﹣2，
∴二次函数解析式为y＝x2﹣2x．
当x＝﹣1时，y＝1+2＝3；
当x＝4时，y＝16﹣2×4＝8；
当x＝1时，y＝1﹣2＝﹣1．
∵x2+bx﹣t＝0相当于y＝x2+bx与直线y＝t的交点的横坐标，
∴当﹣1≤t＜8时，在﹣1＜x＜4的范围内有解．
故答案为：﹣1≤t＜8．
17．解：连结PQ，如图，
∵△ABC为等边三角形，
∴∠BAC＝60°，AB＝AC，
∵线段AP绕点A顺时针旋转60°得到线段AQ，
∴AP＝PQ＝6，∠PAQ＝60°，
∴△APQ为等边三角形，
∴PQ＝AP＝6，
∵∠CAP+∠BAP＝60°，∠BAP+∠BAQ＝60°，
∴∠CAP＝∠BAQ，
在△APC和△ABQ中，
，
∴△APC≌△ABQ，
∴PC＝QB＝10，
在△BPQ中，∵PB2＝82＝64，PQ2＝62，BQ2＝102，
而64+36＝100，
∴PB2+PQ2＝BQ2，
∴△PBQ为直角三角形，∠BPQ＝90°，
∴S四边形APBQ＝S△BPQ+S△APQ＝×6×8+×62＝24+9．
故答案为24+9．

18．解：∵小刚从家出发7分钟时与家的距离是1200米，即小刚从家出发7分钟时距离学校3500﹣1200＝2300m，
∴公交车的速度为：＝400米/分钟，故①正确；
由①知公交车速度为400米/分钟，
∴公交车行驶的时间为＝7分钟，
∴小刚从家出发乘上公交车是在第12﹣7＝5分钟时，故②正确；
∵从上公交车到他到达学校共用10分钟，
∴小刚下公交车后跑向学校的速度是＝100米/分钟，故③正确；
∵小刚从下车至到达学校所用时间为5+10﹣12＝3分钟，
而小刚下车时发现还有4分钟上课，
∴小刚下车较上课提前1分钟，故④错误；
故答案为：①②③
三.解答题
19．解：（1）由方程有两个实数根，可得
△＝b2﹣4ac＝4（k﹣1）2﹣4k2＝4k2﹣8k+4﹣4k2＝﹣8k+4≥0，
解得，k≤；

（2）依据题意可得，x1+x2＝2（k﹣1），x1•x2＝k2，
由（1）可知k≤，
∴2（k﹣1）＜0，x1+x2＜0，
∴﹣x1﹣x2＝﹣（x1+x2）＝x1•x2﹣1，
∴﹣2（k﹣1）＝k2﹣1，
解得k1＝1（舍去），k2＝﹣3，
∴k的值是﹣3．
答：（1）k的取值范围是k≤；（2）k的值是﹣3．
20．解：（1）由于抛物线y＝ax2+bx+c经过A（﹣3，0），B（1，0），可设抛物线的解析式为：y＝a（x+3）（x﹣1），
将C点坐标（0，﹣3）代入，得：
a（0+3）（0﹣1）＝﹣3，解得 a＝1，
则y＝（x+3）（x﹣1）＝x2+2x﹣3，
所以抛物线的解析式为：y＝x2+2x﹣3；

（2）如图1中，连接AC交对称轴于P，

∵PB＝PA，
∴PB+PC＝PB+PA，
∴此时PB+PC最短，△PBC的周长最短，
设直线AC解析式为y＝kx+b，则．
解得，
∴直线AC解析式为y＝﹣x﹣3，
∵对称轴x＝﹣1，
∴点P坐标（﹣1，﹣2）．

（3）在y轴上是存在点M，能够使得△ADM是直角三角形．理由如下：
∵y＝x2+2x﹣3＝y＝（x+1）2﹣4，
∴顶点D的坐标为（﹣1，﹣4），
∵A（﹣3，0），
∴AD2＝（﹣1+3）2+（﹣4﹣0）2＝20．
设点M的坐标为（0，t），分三种情况进行讨论：
①当A为直角顶点时，如图2，

由勾股定理，得AM2+AD2＝DM2，即（0+3）2+（t﹣0）2+20＝（0+1）2+（t+4）2，
解得t＝，
所以点M的坐标为（0，）；
②当D为直角顶点时，如图3，

由勾股定理，得DM2+AD2＝AM2，即（0+1）2+（t+4）2+20＝（0+3）2+（t﹣0）2，
解得t＝﹣，
所以点M的坐标为（0，﹣）；
③当M为直角顶点时，如图4，

由勾股定理，得AM2+DM2＝AD2，即（0+3）2+（t﹣0）2+（0+1）2+（t+4）2＝20，
解得t＝﹣1或﹣3，
所以点M的坐标为（0，﹣1）或（0，﹣3）；
综上可知，在y轴上存在点M，能够使得△ADM是直角三角形，此时点M的坐标为（0，）或（0，﹣）或（0，﹣1）或（0，﹣3）．
21．解：（1）设日销量y与时间t的函数解析式为y＝kt+b
将（1，198），（80，40）代入得：

解得：
∴y＝﹣2t+200（1≤x≤80，t为整数）．
（2）设日销售利润为w，则w＝（P﹣6）y
①当1≤t≤40时
w＝（+16﹣6）（﹣2t+200）
＝﹣（t﹣30）2+2450
∴当t＝30时，日销售利润最大，最大利润是2450元．
②当41≤t≤80时
w＝（﹣t+46﹣6）（﹣2t+200）
＝（t﹣90）2﹣100
∴当t＝41时，日销售利润最大，最大利润为2301元
∵2450＞2301
∴第30天的日销售利润最大，最大利润为2450元．
（3）由（2）得：当1≤t≤40时，w＝﹣（t﹣30）2+2450
令w＝2400，即﹣（t﹣30）2+2450＝2400
解得：t1＝20，t2＝40
由函数w＝﹣（t﹣30）2+2450的二次项系数为负值，对称轴为t＝30，
可知当20≤t≤40时，日销售利润不低于2400元；
当41≤t≤80时，w的最大值为2301，2301＜2400
∴t的取值范围是20≤t≤40时
∴该养殖户有21天利润不低于2400元．
22．解：（Ⅰ）根据题意得，解得
∴抛物线的解析式为y＝x2﹣2x﹣3；

（Ⅱ）如图1，当y＝0时，x2﹣2x﹣3＝0，解得x1＝﹣1，x2＝3，
则C（3，0），
∴OC＝3，
∵B（0，﹣3），
∴OB＝3＝OC，
∴∠OBC＝45°，
由（1）知，y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线的顶点D的坐标为（1，﹣4），
过点D作DE⊥y轴于E，
∴DE＝1，OE＝4，
∴BE＝OE﹣OB＝1＝DE，
∴∠DBE＝45°，
∴∠CBD＝180°﹣∠DBE﹣∠OBC＝90°，
∴△BCD是直角三角形；

（Ⅲ）如图，由抛物线的对称性知，N（2，﹣3），
∴BN＝2，
∵BN∥x轴，PQ⊥x轴，
∴BN⊥PQ，
设P（m，m2﹣2m﹣3）（0＜m＜2），
∵B（0，﹣3），C（3，0），
∴直线BC的解析式为y＝x﹣3，
∴Q（m，m﹣3），
∴PQ＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m＝﹣（m﹣）2+，
∴S四边形BPNQ＝S△PBQ+S△PNQ＝PQ•BN＝ [﹣（m﹣）2+]×2＝﹣（m﹣）2+，
当m＝时，S四边形BPNQ最大，最大值为，此时P（，﹣）．