





初中数学湘教版八年级下册1.2 直角三角形的性质与判定(Ⅱ)背景图课件ppt
展开初中数学湘教版八年级下
《直角三角形的性质和判定Ⅱ》教学设计
课题名 | 直角三角形的性质和判定Ⅱ |
教学目标 | 1.知识与技能: 让学生体验勾股定理的探索过程,并理解掌握勾股定理,学会用勾股定理解决生活中简单的几何问题. 2.过程与方法: 经历操作、归纳和猜想,用面积法推导作出肯定结论的过程,来了解掌握勾股定理. 3.情感态度和价值观:了解我国古代数学家发现、推导和应用勾股定理中的贡献与成就,增进爱国主义情感,体验探索发现的过程和知识运用,增强学习数学的自信。 |
教学重点 | 勾股定理的理解和掌握。 |
教学难点 | 理解勾股定理并能灵活的应用勾股定理解决生活中简单的几何问题。 |
教学准备 | 教师准备:制作《直角三角形的性质和判定Ⅱ》课件。 学生准备:预习《直角三角形的性质和判定Ⅱ》,并准备作图工具及四个全等的直角三角形和一个边长等于直角三角形的斜边的正方形。 |
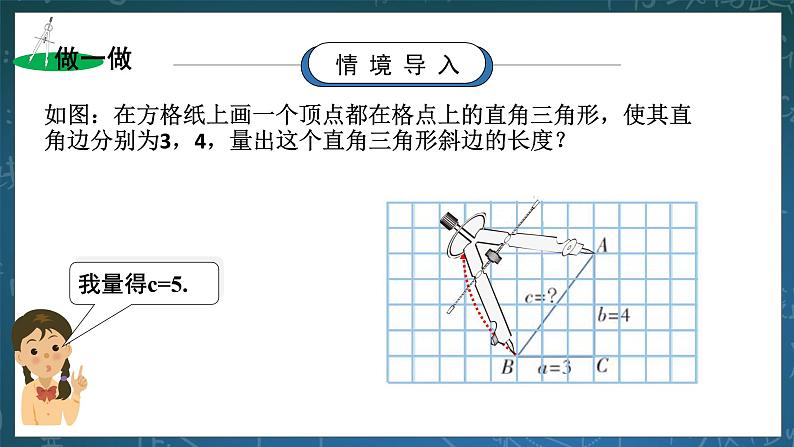
教学过程 | 一、 温故知新 1.教师提问:直角三角形有哪些性质? 学生回答:①角的性质——直角三角形的两个锐角互余;②斜边上的中线性质——直角三角形斜边上的中线等于斜边的一半。③在一个直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。 二、 情境导入 1.如图:在方格纸上画一个顶点都在格点上的直角三角形,使其直角边分别为3,4,量出这个直角三角形斜边的长度? 学生交流测量的方法,并将结果展示。 答:这个直角三角形斜边长为5.
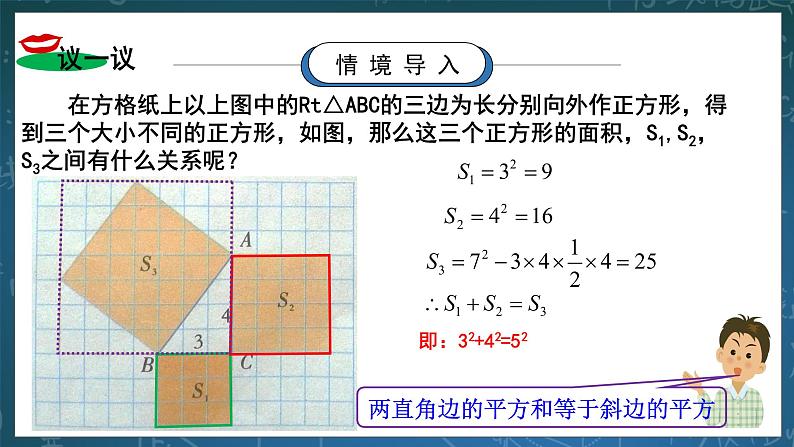
2.在方格纸上以上图中的Rt△ABC的三边为长分别向外作正方形,得到三个大小不同的正方形,如图,那么这三个正方形的面积,S2,S3之间有什么关系呢? 解:S1=32=9, S2=42=16 S3=72-3×4××4=25 ∴S1+S2=S3 §猜想:两直角边的平方和等于斜边的平方。
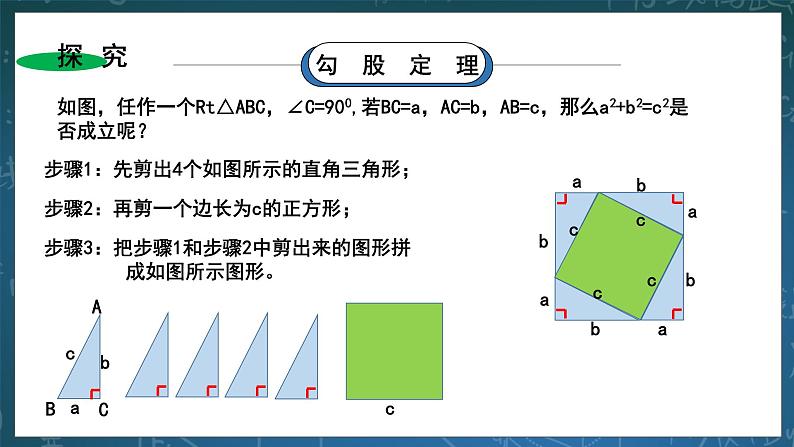
三、新知讲授 (活动一):探究——勾股定理 如图,任作一个Rt△ABC,∠C=900,若BC=a,AC=b,AB=c,那么a2+b2=c2是否成立呢? 步骤1:先剪出4个如图所示的直角三角形;
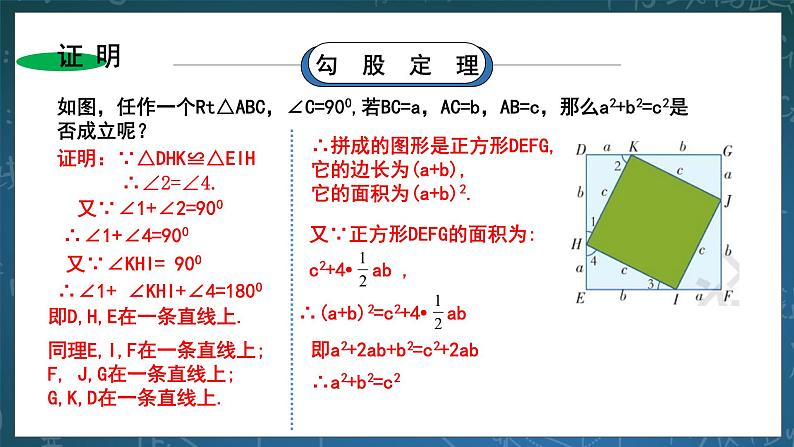
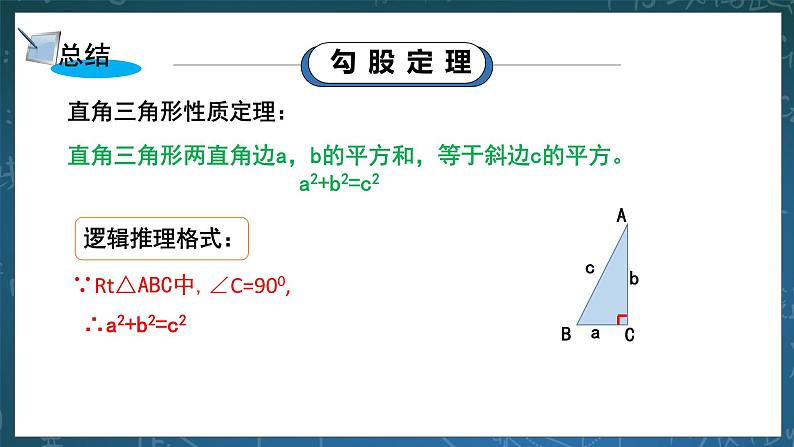
步骤2:再剪一个边长为c的正方形; 步骤3:把步骤1和步骤2中剪出来的图形拼成如图所示图形。 证明:∵△DHK≌△EIH, ∴∠2=∠4. 又∵∠1+ ∠2=900,∴∠1+∠4=900 又∵∠KHI= 900,∴∠1+ ∠KHI+∠4=1800,即D,H,E在一条直线上. 同理可得:E,I,F在一条直线上;F, J,G在一条直线上;G,K,D在一条直线上. ∴拼成的图形是正方形DEFG,它的边长为(a+b),它的面积为(a+b)2. 又∵正方形DEFG的面积为:c2+4• ab , ∴(a+b)2=c2+4•ab,即a2+2ab+b2=c2+2ab ∴a2+b2=c2 (活动二):总结——勾股定理 1.直角三角形性质定理:直角三角形两直角边a,b的平方和,等于斜边c的平方。 即: a2+b2=c2。 2.逻辑推理格式: ∵Rt△ABC中,∠C=900,∴a2+b2=c2 (活动三):读一读——古人的发现 其实我国早在三千多年前就已经知道直角三角形的上述性质,由于古人称直角三角形的直角边中较短的一边为勾,较长的一-边为股,斜边为弦(如图),因此这一性质被称为勾股定理. §规律:勾股定理揭示了直角三角形三边之间的关系.在直角三角形中,若已知直角三角形任意两条边长,我们可以根据勾股定理,求出第三边的长. (活动四):做一做——典例分析 例1 如图,在等腰三角形ABC中,已知AB=AC=13cm,BC=10cm,AD⊥BC于点D,你能算出BC边上的高AD的长吗? 题析:由“AB=AC=13cm,BC=10cm,AD⊥BC”可得:CD=BC=5cm,∠ADC=900。由此,Rt△ADC中,已知了AC,DC,因此就可求出AD. 解:∵在△ABC中,AB=AC=13,BC=10cm, AD⊥BC, ∴CD=BC=5cm ∴在Rt△ADC中,由勾股定理得:AD===12(cm) 即:BC边上的高AD的长为12cm. (活动五):练一练——勾股定理的应用 在Rt△ABC中,∠C=90°. (1)已知a=25, b=15,求c; (2)已知a=5, c=9,求b; 解:在Rt△ABC中,由勾股定理得: 解:在Rt△ABC中,由勾股定理得: c===5 b===2 (3)已知b=5, c=15,求a. 解:在Rt△ABC中,由勾股定理得: a===10 §规律:斜边=;一直角边= (活动六):动脑筋——勾股定理的实际应用 如图,电工师傅把4m长的梯子AC靠在墙上,使梯脚C离墙脚B的距离为1.5m,准备在墙上安装电灯。当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m,即移动到C'处。那么,梯子顶端是否往上移动0.5m呢? 根据题意抽象出示意图。由题意可知:AC=A/C/=4m,BC=1.5m,CC/=0.5m, AA/就是梯子顶端上移的距离。 ∵在Rt△ABC中,∠B=90°,AC=4m, BC=1.5m, ∴BA==≈3.71(m) ∵在Rt△A/BC/中,∠B=90°,A/C/=4m, BC/=BC-CC/=1m, ∴BA/==≈3.87(m) ∴AA/=BA/-BA=3.87-3.71=0.16(M), 即梯子顶端A点大约向上移动了0.16m,而不是向上移动0.5m. (活动七):应用——典例分析 例2 (引葭赴岸问题)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”意思是:有一个边长为10尺的正方形池塘,一棵芦苇生长在池的中央,其出水部分为1尺,如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面,问水深与芦苇长各为多少? 分析:根据题意, 先画出水池截面示意图,设AB为芦苇,BC为芦苇出水部分,即BC=1尺,将芦苇拉向岸边,其顶部B点恰好碰到岸边B/,则AB=AB/,正方形池塘边长为10尺,则CB=5尺。 解:如图, 设水池深为x尺,则AC=x尺,AB=AB/=(x+ 1)尺. 因为正方形池塘边长为10尺,所以B/C=5尺. 在Rt△ACB'中,根据勾股定理,得: x2+52=(x+1)2,解得:x=12. ∴x+1=13(尺),即:芦苇长为13尺。 答:水池的深度为12尺,芦苇长为13尺. §利用勾股定理求线段的长度“四步法”: 1.找直角:找出图中的直角三角形,或作辅助线构造直角三角形。 2.定关系:找出所求线段与直角三角形三边的关系。 3.计算:根据勾股定理计算相关线段的平方。 4.求值:估算所求数值是哪个数的平方,然后确定线段长度。 三、课堂小测: 1. 如图,一艘渔船以30海量/h的速度由西向东追赶鱼群,在A处测得小岛C在船的北偏东600方向;40min后,渔船行至B处,此时测得小岛C在船的北偏东300方向,已知以小岛C为中心,周围10海里以内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险? 分析:判定是否有触礁危险,只需看点C到航线AE的距离是否大于10海里:大于无危险,小于有危险。 解:过点C作CE⊥AB,交AB的延长线于点E,则由题意可得: ∠CAE=900-600=300,∠CBE=900-300=600,AB=30×=20(海里) ∴∠ACB=∠CBE-∠CAE=300=∠CAE, ∴BC=AB=20海里 又∵在Rt△BEC中,∠BEC=900,∠BCE=900-∠CBE=300 ∴BE=BC=10海里 ∴CE==10海里>10海里 ∴艘渔船继续向东追赶鱼群没有触礁的危险。
解:过点D作DF⊥AE于点F,则由题意可得: AE=12m,AF=BD=6m,DF=AB=8m,FE=AE-AF=6m,∠BCD=600, 又∵在Rt△DEF中,∠DFE=900, ∴DE===10(m) 又∵在Rt△DBC中,∠CBD=900,∠BDC=900-∠DCB=300 ∴BC=DC,设DC=xm,则BC=m,依题意可得方程 : 62+(x)2=x2,解得:x=,即DC=m ∴ED+CD=10+(m) 答:电线CDE的总长(10+)m. 四、你的收获: 1.勾股定理:直角三角形两直角边a,b的平方和,等于斜边c的平方。即:a2+b2=c2。 2.利用勾股定理求线段的长度:在直角三角形中,若已知直角三角形任意两条边长,我们可以根据勾股定理,求出第三边的长. |
布置作业 | 课堂作业:P16 习题1.2 第3、4题。 家作:P16 习题1.2第1、2题并预习P14~16《直角三角形的性质和判定Ⅱ》。 |
板书设计 | |
教学反思 | 本节课从复习直角三角形的性质开始,然后通过拼、量、逻辑推理探究了勾股定理,并运用勾股定理解决生活中的实际问题。其中,运用勾股定理解决生活中的实际问题是教学的难点。在教学中,通过实例,运用割补法,找图中的直角三角形或作辅助线构造直角三角形,将图形转化成特殊图形,从而化难为易,激发学生兴趣,培养学生的分析能力和逻辑推理能力,加深学生对知识的理解的运用。 |
初中湘教版1.2.1数轴优质课ppt课件: 这是一份初中湘教版1.2.1数轴优质课ppt课件,文件包含湘教版七上数学121数轴课件pptx、湘教版七上数学121数轴教案doc等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学1.2 直角三角形的性质与判定(Ⅱ)示范课ppt课件: 这是一份初中数学1.2 直角三角形的性质与判定(Ⅱ)示范课ppt课件
初中数学湘教版八年级下册第1章 直角三角形1.2 直角三角形的性质与判定(Ⅱ)教案配套ppt课件: 这是一份初中数学湘教版八年级下册第1章 直角三角形1.2 直角三角形的性质与判定(Ⅱ)教案配套ppt课件,文件包含湘教版八下数学12直角三角形的性质和判定Ⅱ勾股定理课件pptx、湘教版八下数学12直角三角形的性质和判定Ⅱ勾股定理教案docx等2份课件配套教学资源,其中PPT共26页, 欢迎下载使用。














