2021-2022学年北京市大兴区九年级（上）期末数学试卷（含答案解析）

这是一份2021-2022学年北京市大兴区九年级（上）期末数学试卷（含答案解析），共21页。试卷主要包含了【答案】A，【答案】B，【答案】D，【答案】C，【答案】x1=0，x2=3等内容，欢迎下载使用。
下列图形中，既是中心对称图形也是轴对称图形的是( )
A. 圆B. 平行四边形C. 直角三角形D. 等边三角形
抛物线y=(x+1)2+2的顶点坐标是( )
A. (1,2)B. (1,−2)C. (−1,2)D. (−1,−2)
以下事件为随机事件的是( )
A. 通常加热到100℃时，水沸腾B. 篮球队员在罚球线上投篮一次，未投中
C. 任意画一个三角形，其内角和是360∘D. 半径为2的圆的周长是4π
如图，△ABC中，∠ABC=50∘，∠ACB=74∘，点O是△ABC的内心．则∠BOC等于( )
A. 124∘
B. 118∘
C. 112∘
D. 62∘
下列所给方程中，没有实数根的是( )
A. x2+2x=0B. 5x2−4x−2=0
C. 3x2−4x+1=0D. 4x2−3x+2=0
将二次函数y=x2−4x+5化为y=x−h2+k的形式，结果为( )
A. y=x−22+1B. y=x+22+1C. y=x−42+1D. y=x+42+1
如图，⊙C与∠AOB的两边分别相切，其中OA边与⊙C相切于点P ，若∠AOB=90∘，OP=4，则OC的长为( )
A. 8B. 162C. 42D. 22
小亮、小明、小刚三名同学中，小亮的年龄比小明的年龄小2岁，小刚的年龄比小明的年龄大1岁，并且小亮与小刚的年龄的乘积是130.你知道这三名同学的年龄各是多少岁吗？设小明的年龄为x岁，则可列方程为( )
A. (x+2)(x−1)=130B. (x−2)(x+1)=130
C. x(x−2)=130D. x(x+1)=130
一元二次方程x2−3x=0的根是__________.
如图，A，B，C是⊙O上的三个点，若∠AOB=70∘，则∠C=__________.
已知抛物线y=x2−x−3经过点A(2,y1)、B(3,y2)，则y1与y2的大小关系是__________.
如图，将△AOB绕点O按逆时针方向旋转45∘后得到△A′OB′，若∠AOB=15∘，则∠AOB′的度数是__________.
圆心角是270∘的扇形的半径为4cm，则这个扇形的面积是__________cm2.
请写出一个开口向上，并且对称轴为直线x=1的抛物线的表达式y=__________.
若一个扇形的半径是18cm，且它的弧长是6πcm，则此扇形的圆心角等于__________.
已知点A的坐标为(a,b)，O为坐标原点，连接OA，将线段OA绕点O顺时针旋转90∘得到线段OA1，则点A1的坐标为 −−−−.
计算：27+(3−π)0+|1−3|+3×13.
在平面直角坐标系xOy中，二次函数y=x2−2mx+5m的图象经过点(1,−2).
(1)求二次函数的表达式；
(2)求二次函数图象的对称轴．
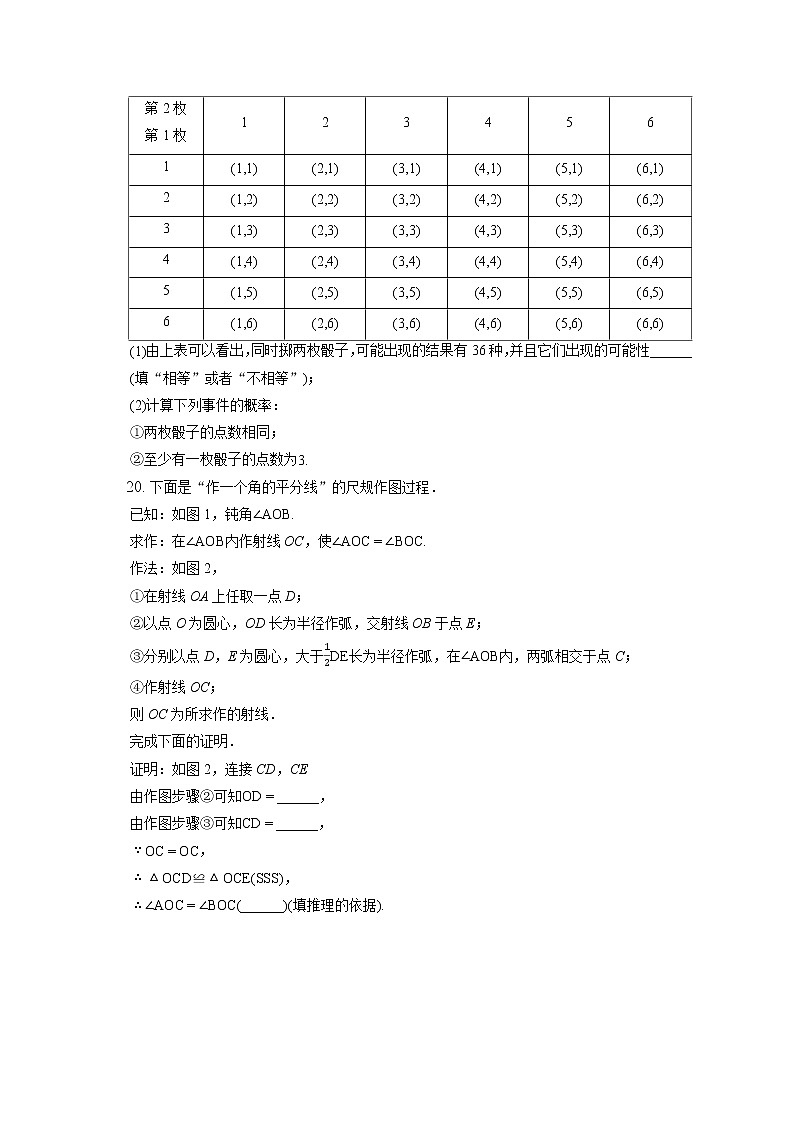
同时掷两枚质地均匀的骰子，两枚骰子分别记为第1枚和第2枚，下表列举出了所有可能出现的结果．
(1)由上表可以看出，同时掷两枚骰子，可能出现的结果有36种，并且它们出现的可能性______(填“相等”或者“不相等”)；
(2)计算下列事件的概率：
①两枚骰子的点数相同；
②至少有一枚骰子的点数为3.
下面是“作一个角的平分线”的尺规作图过程．
已知：如图1，钝角∠AOB.
求作：在∠AOB内作射线OC，使∠AOC=∠BOC.
作法：如图2，
①在射线OA上任取一点D；
②以点O为圆心，OD长为半径作弧，交射线OB于点E；
③分别以点D，E为圆心，大于12DE长为半径作弧，在∠AOB内，两弧相交于点C；
④作射线OC；
则OC为所求作的射线．
完成下面的证明．
证明：如图2，连接CD，CE
由作图步骤②可知OD=______，
由作图步骤③可知CD=______，
∵OC=OC，
∴△OCD≌△OCE(SSS)，
∴∠AOC=∠BOC(______)(填推理的依据).
如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E.
(1)求证：∠BCO=∠D；
(2)若CD=42，OE=1，求⊙O的半径．
已知关于x的一元二次方程x2−3x+2a−1=0有两个不相等的实数根．
(1)求a的取值范围；
(2)若a为正整数，求方程的根．
某超市按每袋20元的价格购进某种软糖，在销售过程中发现，该种软糖每天的销售量w(袋)与销售单价x(元)满足w=−2x+80(20≤x≤40)，如果销售这种软糖每天的利润为y(元).
(1)求y与x之间的函数关系式；
(2)当软糖销售单价定为每袋多少元时，销售这种软糖每天的利润最大？最大利润是多少？
在平面直角坐标系xOy中，抛物线y=x2−4x−1与y轴交于点A，其对称轴与x轴交于点B，一次函数y=kx+b(k≠0)的图象经过点A，B.
(1)求一次函数的表达式；
(2)当x>−3时，对于x的每一个值，函数y=nx(n≠0)的值大于一次函数y=kx+b的值，直接写出n的取值范围．
已知：如图，在△ABC中，AB=AC，D是BC的中点．以BD为直径作⊙O，交边AB于点P，连接PC，交AD于点E.
(1)求证：AD是⊙O的切线；
(2)若PC是⊙O的切线，BC=8，求PC的长．
在平面直角坐标系xOy中，二次函数y=x2+bx+c的图象经过点(0,−3)，(3,0).
(1)求二次函数的表达式；
(2)将二次函数y=x2+bx+c的图象向上平移n(n>0)个单位后得到的图象记为G，当0≤x≤52时，图象G与x轴只有一个公共点，结合函数的图象，直接写出n的取值范围．
如图，在等腰△ABC中，∠BAC=90∘，点D在线段BC的延长线上，连接AD，将线段AD绕点A逆时针旋转90∘得到线段AE，连接CE，射线BA与CE相交于点F.
(1)依题意补全图形；
(2)用等式表示线段BD与CE的数量关系，并证明；
(3)若F为CE中点，AB=2，则CE的长为______.
在平面直角坐标系xOy中，点M在x轴上，以点M为圆心的圆与x轴交于A(1,0)，B(4,0)两点，对于点P和⊙M，给出如下定义：若抛物线y=ax2+bx+c(a≠0)经过A，B两点且顶点为P，则称点P为⊙M的“图象关联点”．
(1)已知E(5,2)，F(52,−4)，G(3,1)，H(52,3)，在点E，F，G，H中，⊙M的”图象关联点”是______；
(2)已知⊙M的“图象关联点”P在第一象限，若OP=53PM，判断OP与⊙M的位置关系，并证明；
(3)已知C(4,2)，D(1,2)，当⊙M的“图象关联点”P在⊙M外且在四边形ABCD内时，直接写出抛物线y=ax2+bx+c中a的取值范围．
答案和解析
1.【答案】A
【解析】解：A.圆既是中心对称图形，也是轴对称图形，故此选项符合题意；
B.平行四边形是中心对称图形，不是轴对称图形，故此选项不合题意；
C.直角三角形不是中心对称图形，也不一定是轴对称图形，故此选项不合题意；
D.等边三角形是轴对称图形，不是中心对称图形，故此选项不合题意．
故选：A.
根据轴对称图形与中心对称图形的概念求解．
本题考查中心对称图形和轴对称图形的概念，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合，中心对称图形是要寻找对称中心，图形绕对称中心旋转180∘后与原图形重合．
2.【答案】C
【解析】解：∵y=(x+1)2+2为二次函数的顶点式，
∴该抛物线的顶点坐标为(−1,2)，
故选：C.
根据抛物线的顶点式直接得出顶点坐标即可．
本题主要考查二次函数的性质，关键是要能根据顶点式直接写出顶点的坐标．
3.【答案】B
【解析】解：A.通常加热到100℃时，水沸腾，这是必然事件，故A不符合题意；
B.篮球队员在罚球线上投篮一次，未投中，这是随机事件，故B符合题意；
C.任意画一个三角形，其内角和是360∘，这是不可能事件，故C不符合题意；
D.半径为2的圆的周长是4π，这是必然事件，故D不符合题意；
故选：B.
根据必然事件，随机事件，不可能事件的特点判断即可．
本题考查了随机事件，熟练掌握必然事件，随机事件，不可能事件的特点是解题的关键．
4.【答案】B
【解析】解：∵点O是△ABC的内心，
∴OB平分∠ABC，OC平分∠ACB，
∴∠OBC=12∠ABC=12×50∘=25∘，
∠OCB=12∠ACB=12×74∘=37∘，
∴∠BOC=180∘−∠OBC−∠OCB=180∘−25∘−37∘=118∘.
故选：B.
根据三角形内心的性质得到∠OBC=12∠ABC=25∘，∠OCB=12∠ACB=37∘，然后根据三角形内角和计算∠BOC的度数．
本题考查了三角形的内切圆与内心：三角形的内心就是三角形三个内角角平分线的交点，三角形的内心与三角形顶点的连线平分这个内角．
5.【答案】D
【解析】解：A.x2+2x=0，
∵b2−4ac=4>0，
∴方程有实数根，故本选项不符合题意；
B.5x2−4x−2=0，
∵b2−4ac=16+40=56>0，
∴方程有实数根，故本选项不符合题意；
C.3x2−4x+1=0，
∵b2−4ac=16−12=4>0，
∴方程有实数根，故本选项不符合题意；
D.4x2−3x+2=0，
∵b2−4ac=9−32=−23