初中数学苏科版七年级上册第6章 平面图形的认识（一）6.5 垂直同步训练题

这是一份初中数学苏科版七年级上册第6章 平面图形的认识（一）6.5 垂直同步训练题，共47页。
6.5 垂直
1．（2022·江苏常州·七年级期末）点P是直线外一点，为直线上三点，，则点P到直线的距离是（          ）
A．2cm B．小于2cm C．不大于2cm D．4cm
2．（2022·江苏南京·七年级期末）如图，，，垂足分别为C、D，线段的长度是（       ）

A．点A到的距离 B．点B到的距离
C．点C到的距离 D．点D到的距离
3．（2022·江苏无锡·七年级期末）有下列说法：①两条不相交的直线叫平行线；②同一平面内，过一点有且只有一条直线与已知直线垂直；③两条直线相交所成的四个角中，如果有两个角相等，那么这两条直线互相垂直；④有公共顶点的两个角是对顶角．其中说法正确的个数是（          ）
A．1 B．2 C．3 D．4
4．（2022·江苏·南京市第二十九中学七年级期末）下列说法正确的是（     ）
A．不相交的两条直线叫做平行线
B．同一平面内，过一点有且仅有一条直线与已知直线垂直
C．平角是一条直线
D．过同一平面内三点中任意两点，只能画出3条直线
5．（2022·江苏镇江·七年级期末）如图，于O，直线CD经过O，，则的度数是（       ）

A． B． C． D．
6．（2022·江苏宿迁·七年级期末）有下列说法：①两条直线相交所成的四个角中有一个角是直角，则这两条直线互相垂直；②如果同一平面内的两条线段不相交，那么这两条线段所在直线互相平行；③如果一个角的两边与另一个角的两边互相垂直，则这两个角互补；④如果一个角的两边与另一个角的两边互相平行，则这两个角相等，其中正确的有（       ）
A．1个 B．2个 C．3个 D．4个
7．（2022·江苏盐城·七年级期末）小光准备从A地去往B地，打开导航显示两地距离为39.6km，但导航提供的三条可选路线长却分别为52km，53km，56km（如图）．能解释这一现象的数学知识是（       ）

A．两点之间，线段最短 B．两点确定一条直线
C．垂线段最短 D．过一点有且只有一条直线与已知直线垂直
8．（2022·江苏常州·七年级期末）下列说法不正确的是（        ）
A．过任意一点可作已知直线的一条平行线 B．在同一平面内两条不相交的直线是平行线
C．在同一平面内，过直线外一点只能画一条直线与已知直线垂直 D．直线外一点与直线上各点连接的所有线段中，垂线段最短
9．（2022·江苏宿迁·七年级期末）如图，CD⊥AB，垂足是点D，AC=8，BC＝6，CD＝4，点E是线段AB上的一个动点（包括端点），连接CE，那么CE的长为整数值的线段有（　　）

A．3条 B．8条 C．7条 D．5条
10．（2022·江苏淮安·七年级期末）如图，点在直线上，(三点在一条直线上，)若，已知，则________°

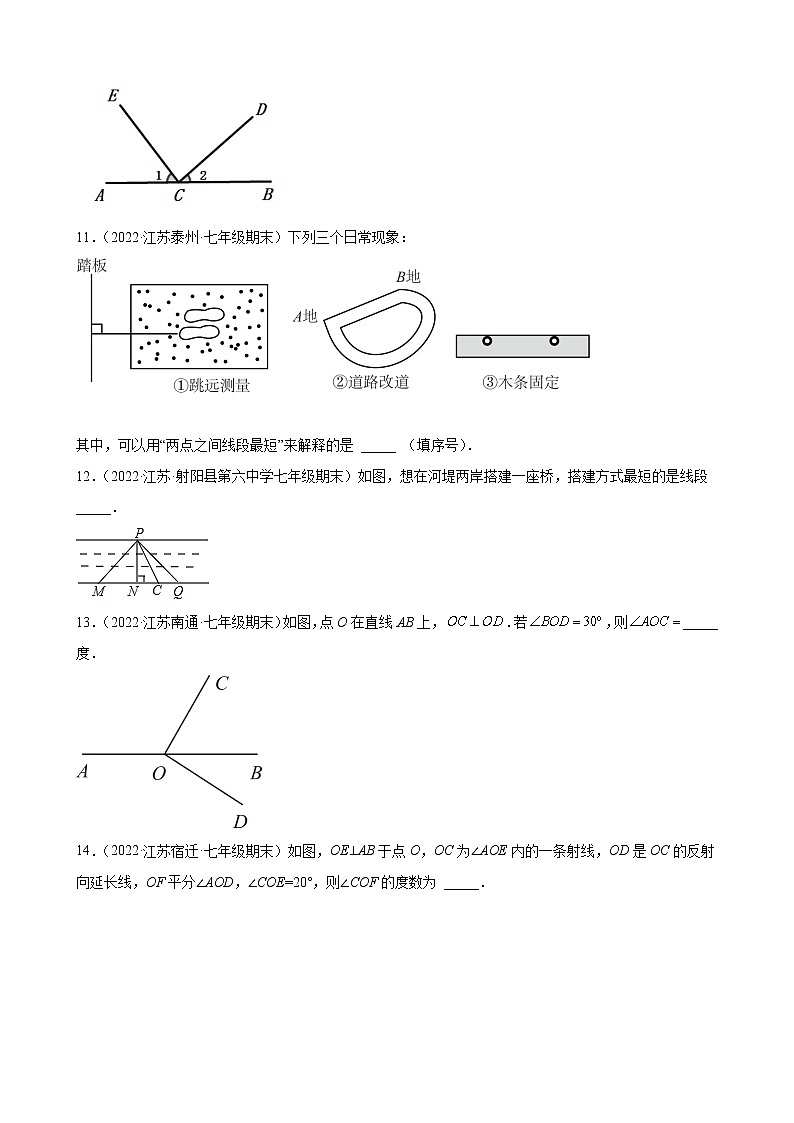
11．（2022·江苏泰州·七年级期末）下列三个日常现象：


其中，可以用“两点之间线段最短”来解释的是 _____ （填序号）．
12．（2022·江苏·射阳县第六中学七年级期末）如图，想在河堤两岸搭建一座桥，搭建方式最短的是线段 _____．

13．（2022·江苏南通·七年级期末）如图，点O在直线AB上，．若，则_____度．

14．（2022·江苏宿迁·七年级期末）如图，OE⊥AB于点O，OC为∠AOE内的一条射线，OD是OC的反射向延长线，OF平分∠AOD，∠COE=20°，则∠COF的度数为 _____．

15．（2022·江苏南京·七年级期末）下列三个日常现象：
①用两根钉子就可以把一根木条固定在墙上；
②把弯曲的公路改直，就能够缩短路程；
③体育课上，老师测量某名同学的跳远成绩．
其中，可以用“两点之间线段最短”来解释的是________ .(填序号)
16．（2022·江苏扬州·七年级期末）如图，点P是∠AOB的边OB上的一个格点．

(1)过点P画OA的垂线，垂足为H；
(2)过点P画OB的垂线，交OA于点C；
(3)线段PH的长度是点P到_____的距离．线段PC、PH、OC这三条线段大小关系是_____（用“＜”号连接），依据是________________________________．
17．（2022·江苏扬州·七年级期末）如图，直线AB、CD相交于点O，已知，OE把分成两个角，且，．

(1)求的度数；
(2)求的度数．
18．（2022·江苏无锡·七年级期末）如图，直线AB、CD相交于点O，射线OE在∠DOB内部，且．过O作OF⊥OE．若，

(1)求∠BOE的度数（用含m的代数式表示）；
(2)若，试说明OB平分∠DOF．
19．（2022·江苏·射阳县第六中学七年级期末）如图，直线AB、CD相交于点O，OE平分∠BOD，∠DOE＝36°，且OE⊥OF．求∠AOC和∠AOF的度数．


20．（2022·江苏宿迁·七年级期末）如图，直线AB、CD相交于O点，∠AOC＝70°，∠BOE=35°，

(1)∠DOE的度数；
(2)若OF平分∠AOD，射线OE与OF之间有什么位置关系？为什么？
21．（2022·江苏宿迁·七年级期末）在如图所示的方格纸上作图并标上相应的字母．

（1）过点P画线段AB的平行线a；
（2）过点P画线段AB的垂线，垂足为H；
（3）点A到线段PH的距离即线段 的长．
22．（2022·江苏南京·七年级期末）如图，△ABC的三个顶点均在格点处．

（1）过点B画 AC 的平行线 BD；
（2）过点A画 BC 的垂线AE；（请用黑水笔描清楚）
23．（2022·江苏宿迁·七年级期末）利用网格画图：


(1)过点C画AB的平行线CD；
(2)过点C画AB的垂线，垂足为E；
(3)连接CA、CB，在线段CA、CB、CE中，线段___________最短．
24．（2022·江苏淮安·七年级期末）如图，在正方形网格中有四个格点O、A、B、C，按要求进行下列作图，并标出相应的字母（要求画图时用2B铅笔加黑加粗）：

(1)画线段AB，画射线CB，画直线AC；
(2)过点A画射线CB的垂线AD，垂足为点D；
(3)过点O画直线AC的平行线OE．
25．（2022·江苏扬州·七年级期末）如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点叫做格点，请利用格点和直尺画图，并完成填空．（画出的点、线请用铅笔描粗描黑）

(1)画线段和直线；
(2)过点画的垂线，垂足为点，并标出经过的格点；
(3)线段长是点______到直线______的距离；
(4)三角形的面积是______．
26．（2022·江苏·射阳县第六中学七年级期末）在如图所示的方格纸中，每个小正方形的顶点称为格点，每个小正方形的边长为1，已知四边形ABCD的四个顶点在格点上，利用格点和直尺按下列要求画图：
（1）过点C画AD的平行线CE；
（2）过点B画CD的垂线，垂足为F．

27．（2022·江苏扬州·七年级期末）如图，已知P，A，B三点，按下列要求完成画图和解答．

(1)作直线AB；
(2)作射线PA，PB，用量角器测量______°．
(3)利用网格过点A作PB的平行线AC；
(4)过点P画于点D；
(5)根据图形回答：在线段PA，PB，PD中，PD的长度最短．理由：______．
28．（2022·江苏泰州·七年级期末）如图，每个小方格都是边长为1的正方形，A、B、C三点都是格点（每个小方格的顶点叫做格点）．


(1)找出格点D，画出AB的平行线CD；
(2)找出格点E，画AB的垂线CE，垂足为H；
(3)图中满足要求的格点D共可以找出_____________个；
(4)线段______________的长是点C到直线AB的距离．
29．（2022·江苏淮安·七年级期末）在如图所示的方格纸中，每个小正方形的顶点称为格点，每个小正方形的边长为1，已知四边形ABCD的四个顶点在格点上，利用格点和直尺按下列要求画图：

(1)过点C画AD的平行线CE；
(2)过点B画CD的垂线，垂足为F．
(3)线段CF表示点 到线段 的距离．
30．（2022·江苏盐城·七年级期末）如图，射线OC端点O在直线AB上，，OE平分．

(1)当时，求的度数；
(2)OC与OE有怎样的位置关系?为什么？
31．（2022·江苏宿迁·七年级期末）如图，直线AB、CD相交于O，OE⊥CD，且∠BOD＝5∠AOD，求∠BOE的度数．

32．（2022·江苏·射阳县第六中学七年级期末）如图，直线AB、CD相交于点O，OE平分∠BOD，OE⊥OF．

(1)若∠DOE＝32°，求∠BOF的度数；
(2)若∠COE：∠COF＝8：3，求∠AOF的度数．
33．（2022·江苏常州·七年级期末）如图，∠AOC=140°，OD平分∠AOC，OB⊥OA，垂足为O．

求∠DOB的度数：（按要求填空）
解：因为OD平分∠AOC(已知)
所以∠AOD=∠AOC(                    )
因为∠AOC=140°（已知）
所以∠AOD=_________°（等量代换）
又因为OB⊥OA(已知)
所以∠AOB=90°(                              )
所以∠DOB=∠AOB-______________=_____________°
34．（2022·江苏扬州·七年级期末）如图，直线、相交于点，平分，，垂足为．

(1)写出的所有余角______；
(2)若，求的度数；
35．（2022·江苏徐州·七年级期末）如图，直线AB、CD相交于点O，∠COE＝90°．

(1)若∠BOD＝35°，则∠BOE＝ °；
(2)若∠BOC＝5∠BOD，求∠AOE的度数；
(3)∠BOD＝20°，过点O作射线OF⊥AB，则∠EOF＝ °．
36．（2022·江苏盐城·七年级期末）如图，直线AB、CD相交于点O，OE⊥CD．

（1）若∠BOD∶∠BOC＝1∶4，求∠AOE的度数；
（2）在第一问的条件下，过点O作OF⊥AB，则∠EOF的度数为 ．
37．（2022·江苏苏州·七年级期末）在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点．△ABC的顶点A、B、C都在格点上．
(1)过B作AC的平行线BD．
(2)作出表示B到AC的距离的线段BE．
(3)线段BE与BC的大小关系是：BE　 　BC(填“＞”、“＜”、“=”)．
(4)△ABC的面积为　 　．

38．（2022·江苏·南京市第二十九中学七年级期末）如图，所有小正方形的边长都为1个单位，A、B、C均在格点上．

(1)过点C画线段AB的平行线CF；
(2)过点A画线段BC的垂线，垂足为G；
(3)过点A画线段AB的垂线，交BC于点H；
(4)线段 的长度是点H到直线AB的距离；
(5)线段AG、AH、BH的大小关系是 （用“＜”连接），理由是 ．
39．（2022·江苏南京·七年级期末）如图，方格纸中每个小正方形的边长为1，点A、B、C均为格点．

(1)根据要求画图：①过点C画；②过点C画，垂足为D；
(2)图中线段______的长度表示点A到直线CD的距离；
(3)比较线段CA、CD的大小关系是______．
40．（2022·江苏盐城·七年级期末）如图，汽车站、高铁站分别位于A、B两点，直线a和b分别表示公路与铁路．

（1）从汽车站到高铁站怎样走最近？画出图形，理由是 ．
（2）从高铁站到公路怎样走最近？画出图形，理由是 ．
41．（2022·江苏苏州·七年级期末）几何知识可以解决生活中许多距离最短的问题．让我们从书本一道习题入手进行知识探索．
【回忆】
如图，A、B是河l两侧的两个村庄．现要在河l上修建一个抽水站C，使它到A、B两村庄的距离的和最小，请在图中画出点C的位置，并说明理由．

【探索】
（1）如图，A、B两个村庄在一条笔直的马路的两端，村庄 C在马路外，要在马路上建一个垃圾站O，使得AO+BO+CO最小，请在图中画出点O的位置，并说明理由．

（2）如图，A、B、C、D四个村庄，现建一个垃圾站O，使得AO+BO+CO+DO最小，请在图中画出点O的位置，并说明理由．

42．（2022·江苏泰州·七年级期末）如图，用三张卡片拼成如下图①，图②所示的两个四边形，其周长分别为、．

(1)请你根据所学知识解释：在直角三角形卡片中，“”的理由是_________．（填写正确选项的字母）
A．两点之间线段最短；B．过一点有且只有一条直线与已知直线垂直；C．垂线段最短；D．两点确定一条直线．
(2)分别计算、（用含m、n的代数式表示）；
(3)比较与的大小，并说明理由．
43．（2022·江苏泰州·七年级期末）如图，在6×6的正方形网格中，点P是的边OB上的一点．


(1)过点P画OA的垂线，垂足为H；
(2)过点P画OB的垂线，交OA于点C；
(3)线段PH的长度是点P到直线______的距离，线段______的长度是点C到直线OB的距离；
(4)线段PC、PH、OC这三条线段大小关系是______．（用“＜”号连接）
44．（2022·江苏南京·七年级期末）在如图所示的方格纸中，每个小正方形的顶点都叫做格点. 已知点A、B、C均在格点上．

(1)借助方格纸过点B画线段AC的平行线BD；
(2)借助方格纸过点B画线段AC的垂线BE，垂足为E；
(3)观察所画图形，点A到直线BE的距离是线段 的长度；
(4)BD与BE的位置关系是 ；
(5)比较大小：线段AB 线段BE（填“＞”、“＜”或“＝”），理由是 ．
45．（2022·江苏淮安·七年级期末）如图，直线AB、CD相交于点O，过点O作OE⊥AB，射线OF平分∠AOC，∠AOF＝25°．

求：（1）∠BOD的度数；
（2）∠COE的度数．

参考答案：
1．C
【解析】根据“直线外一点到直线上各点的所有线段中，垂线段最短”进行解答．
解：∵直线外一点与直线上各点连接的所有线段中，垂线段最短，且，
∴点到直线的距离不大于，
故选：C．
本题考查了垂线段最短的性质，熟记性质是解题的关键．
2．C
【解析】根据点到直线的距离等于垂线段的长度即可求解．
解：依题意，，，
点A到的距离是线段的长度,
点B到的距离是线段的长度,
点C到的距离是线段的长度
点D到的距离图中没有标出，
故选C
本题考查了点到直线的距离的定义，数形结合以及理解定义是解题的关键．点到直线的距离的等于垂线段的长度．
3．A
【解析】根据平行线的定义、垂直的定义及垂线的唯一性、对顶角的含义即可判断．
同一平面内不相交的两条直线叫做平行线，故说法①错误；说法②正确；两条直线相交所成的四个角中，如果有一个角是直角，那么这两条直线互相垂直，当这两个相等的角是对顶角时则不垂直，故说法③错误；根据对顶角的定义知，说法④错误；故正确的说法有1个；
故选：A
本题考查了两条直线的位置关系中的相关概念及性质，掌握这些概念是关键．
4．B
【解析】根据平行线的定义，垂直的性质，平角的定义，两点确定一条直线的性质依次判断．
解：同一平面内，不相交的两条直线叫做平行线，故选项A错误；
同一平面内，过一点有且仅有一条直线与已知直线垂直，故选项B正确；
平角是角的两边在同一直线上的角，故选项C错误；
过同一平面内三点中任意两点，能画出1条或3条直线故选项D错误；
故选：B．
此题考查语句的正确性，正确掌握平行线的定义，垂直的性质，平角的定义，两点确定一条直线的性质是解题的关键．
5．B
【解析】由OA⊥OB，得出∠AOB=90°，再根据∠AOD=35°，由余角的定义可得出∠BOD，再根据补角的定义可得出∠BOC的度数．
解：∵OA⊥OB，
∴∠AOB=90°，
∵∠AOD=35°，
∴∠BOD=90°-35°=55°，
∴∠BOC=180-55°=125°，
故选B．
本题考查了垂线的定义，平角的定义，关键是利用90°和180°的数据进行计算．
6．A
【解析】根据垂直的定义、平行线的定义和性质、角与角之间的关系，即可得出答案．
解：①是垂直的定义，所以①正确；
②如果同一平面内的两条线段不相交，那么这两条线段所在直线互相平行或相交，故本选项错误；
③如果一个角的两边与另一个角的两边互相垂直，那么这两个角的关系是相等或互补，故本选项错误；
④如果一个角的两边与另一个角的两边互相平行，则这两个角相等或互补，故本选项错误．
故选：A．
掌握垂直的定义、平行线的定义和性质、角与角之间的关系，熟知相关定义是解题的关键．
7．A
【解析】根据线段的性质可得答案．
解：打开导航显示两地距离为39.6km，但导航提供的三条可选路线长却分别为52km，53km，56km（如图）．能解释这一现象的数学知识是两点之间，线段最短．
A、故选项正确，符合题意；
B、故选项错误，不符合题意；
C、故选项错误，不符合题意；
D、故选项错误，不符合题意．
故选：A．
此题考查了线段的性质，解题的关键是熟记线段的性质并应用．
8．A
【解析】根据平行线的事实，垂线的性质一一判定即可．
在同一平面内，过直线外一点有且只有一条直线与已知直线平行，故A不正确；
在同一平面内两条不相交的直线是平行线，这是平行线的概念，故B正确；
在同一平面内，过直线外一点只能画一条直线与已知直线垂直，故C正确；
直线外一点与直线上各点连接的所有线段中，垂线段最短，故D正确；
故选：A．
本题考查了平行线的事实，垂线的性质，解决此题的关键是掌握相关概念性质．
9．C
【解析】根据垂线段最短解答即可．
解：∵CD⊥AB，垂足是点D，AC=8，BC=6，CD=4，
∴CE长的范围是4≤CE≤8，
当点E由A向B运动时，所得线段长度分别为：8、7、6、5、4、5、6
∴CE的长为整数值的线段有7条，
故选C．
此题考查了垂线段最短，关键是熟练掌握垂线段最短的性质．
10．40
【解析】根据平角的定义,再根据垂直的定义，再由即可求出∠2的度数．
解：因为三点在一条直线上，
所以,
因为，
所以，
因为
所以，即．
故答案为：40．
本题考查平角的定义和垂直的定义．熟练理解这些基本知识是解决此题的关键．
11．②．
【解析】利用线段的性质进行解答即可．
解：图①利用垂线段最短；
图②利用两点之间线段最短；
图③利用两点确定一条直线；
故答案为：②．
本题主要考查了线段的性质，熟悉相关性质是解题的关键．
12．PN
【解析】根据从直线外一点到这条直线上各点所连的线段中，垂线段最短可知搭建方式最短的是PN，理由垂线段最短．
解：因为PN⊥MQ，垂足为N，则PN为垂线段，
根据垂线段最短，可得线段PN最短，
故答案为：PN．
本题考查了垂线段最短，利用垂线段的性质是解题关键．
13．120
【解析】根据图示，利用垂直求出∠BOC的度数，然后利用平角，求出∠AOC的度数．
解：∵，
∴∠COD=90°，
∵，
∴∠BOC=∠COD-∠BOD=60°，
∴∠AOC=180°-∠BOC=120°．
故答案为：120．
此题考查角的运算，运用平角和垂直的定义是解题的关键．
14．125°##125度
【解析】先求出∠AOC，再根据邻补角的定义求出∠AOD，然后根据角平分线的定义求出∠AOF即可求解．
解：∵OE⊥AB于点O，
∴∠AOE=90°，
∵∠COE=20°，
∴∠AOC=90°-20°=70°，
∴∠AOD=180°-70°=110°，
∵OF平分∠AOD，
∴∠AOF=∠AOD=55°，
∴∠COF=∠AOC+∠AOF=70°+55°=125°，
故答案为：125°．
本题考查了垂线的定义，角的和差，角平分线的定义，数形结合是解答本题的关键．
15．②
解：①用两根钉子就可以把一根木条固定在墙上，根据两点确定一条直线；

②把弯曲的公路改直，就能够缩短路程，根据两点之间线段最短；
③体育课上，老师测量某个同学的跳远成绩，根据垂线段最短；
故答案为②．
16．(1)见解析
(2)见解析
(3)OA，PH