初中数学苏科版七年级上册第6章 平面图形的认识（一）6.3 余角 补角 对顶角课前预习课件ppt

这是一份初中数学苏科版七年级上册第6章 平面图形的认识（一）6.3 余角 补角 对顶角课前预习课件ppt，共27页。PPT课件主要包含了学习目标，探究新知，同角的补角相等，新知三对顶角等内容，欢迎下载使用。

1. 余角和补角(重点)；2. 余角、补角的性质；3. 对顶角.
新知一 余角和补角（重点）
1.定义(1)如果两个角的和是一个直角，那么这两个角互为余角，简称互余，其中的一个角是另一个角的余角 .(2)如果两个角的和是一个平角，那么这两个角互为补角，简称互补，其中的一个角是另一个角的补角 .
特别解读(1)互余、互补是指两个角之间的数量关系，它们是成对出现的.(2)若两个角互余，则两个角都是锐角；若两个角互补，则两个角可能都是直角，也可能一个角是锐角，另一个角是钝角.(3)互余、互补只与数量有关，与位置无关，若将直角分成两个角，则这两个角互余，若将平角分成两个角，则这两个角互补.
2.计算(1) ∠ α 的余角：90° － ∠ α；(2) ∠ α 的补角：180° － ∠ α.
3. 符号语言(1)如图 6.3 － 1，因为∠ α 与∠ β 互为余角，所以∠ α ＋∠ β=90° . 或者因为∠ α ＋∠ β=90°，所以∠ α 与∠ β 互为余角 .(2)如图 6.3 － 2，因为∠ α 与∠ β 互为补角，所以∠ α ＋∠ β=180° . 或者因为∠ α ＋∠ β=180°，所以∠ α 与∠ β 互为补角 .
4. 一个角的余角(或补角)可以有多个，但它们的度数是相等的， 互余、互补是指具有一定数量关系的两个角 .
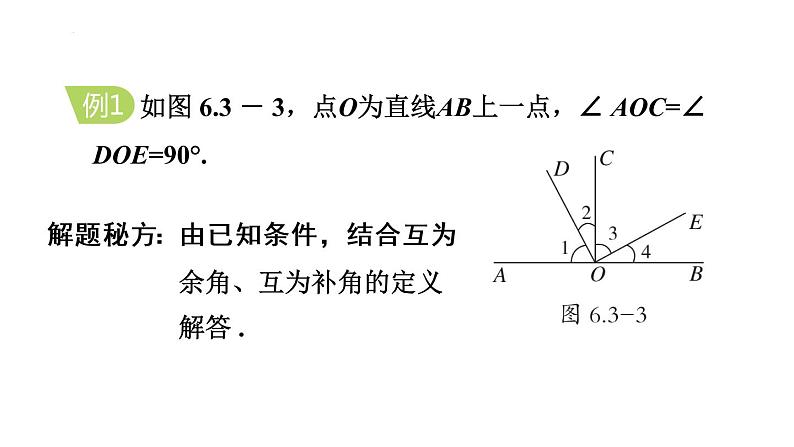
如图 6.3 － 3，点O为直线AB上一点，∠ AOC=∠ DOE=90°.
解题秘方：由已知条件，结合互为余角、互为补角的定义解答 .
方法点拨从图形中找互余或互补的角，可从两个方面进行：一个方面从角的度数入手，和为90°互余，和为180°互补；注意，互余或互补的角不一定都是相邻的两个角；另一个方面从整体入手，由直角分成的两个角互余，由平角分成的两个角互补.最后要结合角的数量关系，利用相等的角进行代换，即可找出所有互余或互补的两个角.
(1)图中互余的角有几对？各是哪些？
解：因为点 O 为直线 AB 上一点，所以∠ BOC+ ∠ AOC=180°(平角的定义).因为∠ AOC=90°，所以∠ 1+ ∠ 2=90°，∠ BOC=180°－ ∠ AOC=180°－90°= 90°，所以∠ 3+ ∠ 4=90°，又因为∠ DOE=90°，所以∠ 2+ ∠ 3=90°，∠ 1+ ∠ 4=90°，所以图中互余的角有 4 对，分别是∠ 1 和∠ 2，∠ 2 和∠ 3，∠ 3 和∠ 4，∠ 1 和∠ 4.
(2)图中互补的角有几对？各是哪些？
解：由已知得，∠ 1+ ∠ BOD=180°，∠ 4+ ∠ AOE=180°，由(1)易知，∠ 1= ∠ 3，∠ 2= ∠ 4，所以∠ 3+ ∠ BOD=180°，∠ 2+ ∠ AOE=180°.又因为∠ AOC+ ∠ BOC=180°，∠ AOC+ ∠ DOE=180°，∠ DOE+ ∠ BOC=180°，
所以图中互补的角有 7 对， 分 别 是 ∠ 1 和 ∠ BOD，∠ 4 和∠ AOE，∠ 3 和∠ BOD，∠ 2 和∠ AOE，∠ AOC 和∠ BOC，∠ AOC 和∠ DOE，∠ DOE 和∠ BOC.
新知二 余角、补角的性质
1.余角的性质 同角(等角) 的余角相等 .(1)同角的余角相等， 符号语言： 因为 ∠ A+ ∠ B=90°，∠ A+ ∠ C=90°，所以∠ B= ∠ C.(2)等角的余角相等， 符号语言： 因为 ∠ A+ ∠ B=90°，∠ D+∠ C=90°，∠ A= ∠ D，所以∠ B= ∠ C.
2. 补角的性质 同角(等角) 的补角相等 .(1)同角的补角相等， 符号语言： 因为 ∠ A+ ∠ B=180°，∠ A+∠ C=180°，所以∠ B= ∠ C.(2)等角的补角相等，符号语言：因为∠ A+ ∠ B=180°，∠ D+ ∠ C=180°，∠ A= ∠ D，所以 ∠ B= ∠ C.
特别提醒(1)如果互补的两个角相等，那么这两个角都是直角.(2)“同角” 指同一个角，“等角”指度数相等的角.(3)余角、补角的性质是说明两个角相等的重要依据.
如图 6.3 － 4，直线 AB 与∠ COD 的两边 OC， OD 分别相交于点 E， F，∠ 1+ ∠ 2=180° . 找出图中与∠ 2 相等的角，并说明理由 .
解题秘方：先找出与∠ 1 和∠ 2互补的角，然后利用互补的关系找出与∠ 2 相等的角 .
解：因为∠ 1+ ∠ 3=180°，∠ 1+ ∠ 2=180°，所以∠ 3= ∠ 2.因为∠ 1+ ∠ 4=180°，∠ 1+ ∠ 2=180°，所以∠ 4= ∠ 2.因为∠ 2+ ∠ 5=180°，∠ 6+ ∠ 5=180°，所以∠ 2= ∠ 6.所以图中与∠ 2 相等的角有∠ 3，∠ 4，∠ 6.
易错警示书写余角、补角的性质符号语言时，不需要再书写等式的性质的符号语言，例如：因为∠ 1+ ∠ 4=180°，∠ 1+ ∠ 2=180°，所以∠ 4=180° － ∠ 1，∠ 2=180° － ∠ 1.所以∠ 2= ∠ 4.根据余角的性质，横线上内容可以省略不写．
1.定义 如图 6.3－5，直线 a、 b 相交成四个角，其中∠ 1 与∠ 2 两个角有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角 .
特别提醒： 对顶角是成对出现的，指两个角之间的位置关系，一个角的对顶角只有一个 .
2. 性质 对顶角相等 .特别提醒： (1)两个角互为对顶角，它们一定相等；(2)相等的两个角不一定是对顶角；(3)符号语言：因为∠ 1 与∠ 2 是对顶角，所以∠ 1= ∠ 2.
特别解读(1)如图 6.3 － 6：图 1 中∠ 1与∠ 2的一边互为反向延长线，另一边不是互为反向延长线， 图2中∠ 1与∠ 2 没有公共顶点，所以都不是对顶角．(2) 互为对顶角的两个角的关系① 位置关系：有公共顶点，两边互为反向延长线.② 数量关系：对顶角相等.
如图 6.3 － 7，直线 AE 与 CD 相交于点 O， OC 平分∠ AOB：
(1)请找出图中∠ 3 的对顶角；
解题秘方：根据对顶角的位置特征找对顶角；
解：∠ 3 的对顶角是∠ 2.
(2)若∠ 3=25°，求∠ 1 的度数 .
解题秘方：根据对顶角相等及角平分线的定义求未知角的度数 .
解：由对顶角相等，得∠ 2= ∠ 3=25°，因为 OC 平分∠ AOB，所以∠ 1= ∠ 2=25° .
方法技巧进行角的计算时， “对顶角相等”这个结论常常被用来将要求的图 1 中∠ 1与∠ 2的角和特征相同的两个角转化成与已知条件相关的角来求解，即对顶角构建了一个已知条件和待求结论之间的“桥梁”.