高中数学湘教版（2019）必修 第一册第4章 幂函数、指数函数和对数函数4.1 实数指数幂和幂函数多媒体教学ppt课件

4.1.3　幂函数

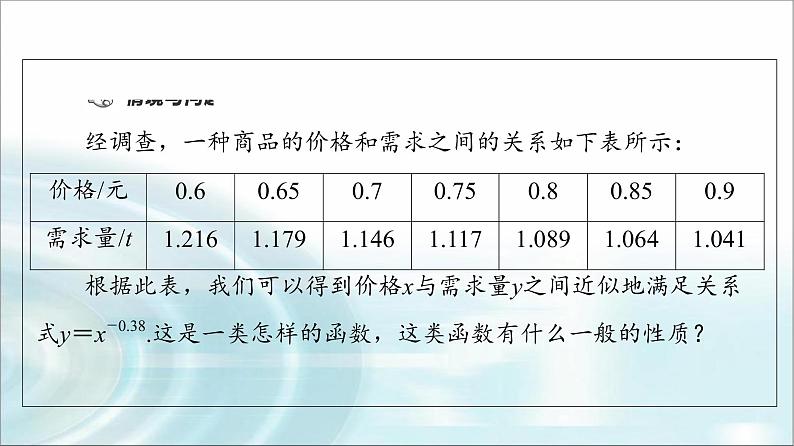
经调查，一种商品的价格和需求之间的关系如下表所示：

根据此表，我们可以得到价格x与需求量y之间近似地满足关系式y＝x－0.38.这是一类怎样的函数，这类函数有什么一般的性质？

知识点1　幂函数的概念

一般来说，当x为自变量而α为非零实数时，函数y＝xα叫作(α次)幂函数．

如何判断一个函数是幂函数？

[提示]　(1)xα的系数为1；(2)x为自变量；(3)α为非零实数．

1．(多选题)下列函数中是幂函数的是(　　)

A．y＝　　　　 B．y＝x3

C．y＝3x D．y＝x－1

ABD　[只有y＝3x不符合幂函数y＝xα的形式，故选ABD．]

2.已知幂函数f(x)＝xα的图象过点，则f(4)＝_____．

　[由f(2)＝可知2α＝，即α＝－1，

∴f(4)＝4－1＝.]

知识点2　幂函数的图象

在同一平面直角坐标系中，画出幂函数y＝x，y＝x2，y＝x3，y＝x，y＝x－1的图象如图所示：

3.思考辨析(正确的打“√”，错误的打“×”)

(1)幂函数的图象都过点(0，0)，(1，1)． (　　)

(2)幂函数的图象一定不能出现在第四象限． (　　)

[答案]　(1)×　(2)√

4.如图所示，给出4个幂函数的图象，则图象与函数的大致对应是(　　)

A．①y＝x，②y＝x2，③y＝x，④y＝x－1

B．①y＝x3，②y＝x2，③y＝x，④y＝x－1

C．①y＝x2，②y＝x3，③y＝x，④y＝x－1

D．①y＝x3，②y＝x，③y＝x2，④y＝x－1

B　[因为y＝x3的定义域为R且为奇函数，故应为图①；y＝x2为开口向上的抛物线且顶点为原点，应为图②.同理可得出选项B正确．]

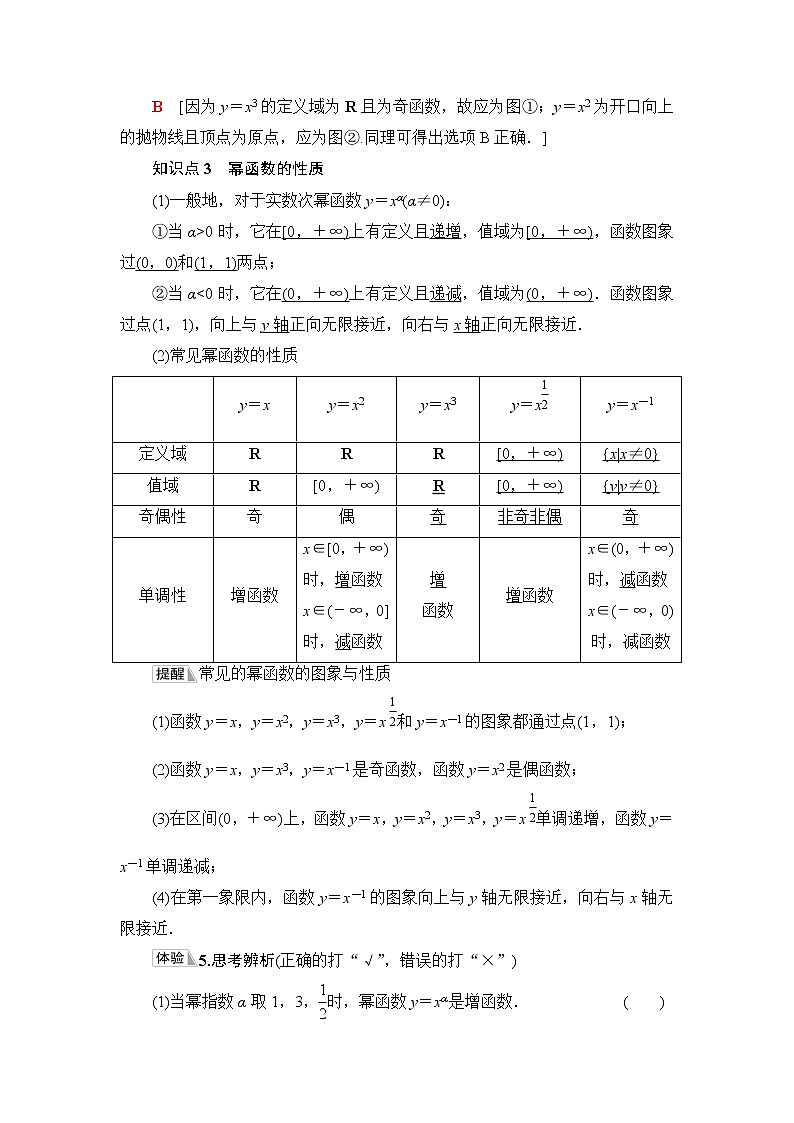
知识点3　幂函数的性质

(1)一般地，对于实数次幂函数y＝xα(α≠0)：

①当α>0时，它在[0，＋∞)上有定义且递增，值域为[0，＋∞)，函数图象过(0，0)和(1，1)两点；

②当α<0时，它在(0，＋∞)上有定义且递减，值域为(0，＋∞)．函数图象过点(1，1)，向上与y轴正向无限接近，向右与x轴正向无限接近．

(2)常见幂函数的性质

常见的幂函数的图象与性质

(1)函数y＝x，y＝x2，y＝x3，y＝x和y＝x－1的图象都通过点(1，1)；

(2)函数y＝x，y＝x3，y＝x－1是奇函数，函数y＝x2是偶函数；

(3)在区间(0，＋∞)上，函数y＝x，y＝x2，y＝x3，y＝x单调递增，函数y＝x－1单调递减；

(4)在第一象限内，函数y＝x－1的图象向上与y轴无限接近，向右与x轴无限接近．

5.思考辨析(正确的打“√”，错误的打“×”)

(1)当幂指数α取1，3，时，幂函数y＝xα是增函数． (　　)

(2)当幂指数α＝－1时，幂函数y＝xα在定义域上是减函数． (　　)

[答案]　(1)√　(2)×

类型1　幂函数的概念

【例1】　已知y＝(m2＋2m－2)x＋2n－3是幂函数，求m，n的值．

[解]　由题意得

解得

所以m＝－3，n＝.

,

判断一个函数是否为幂函数的方法

判断一个函数是否为幂函数的依据是该函数是否为y＝xα(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1．

1．在函数y＝，y＝2x2，y＝x2＋x，y＝1中，幂函数的个数为(　　)

A．0　 B．1　　　　

C．2　　　　 D．3

B　[∵y＝＝x－2，

∴是幂函数；

y＝2x2由于出现系数2，因此不是幂函数；

y＝x2＋x是两项和的形式，不是幂函数；

y＝1＝x0(x≠0)，可以看出，常函数y＝1的图象比幂函数y＝x0的图象多了一个点(0，1)，所以常函数y＝1不是幂函数．]

类型2　幂函数的图象及应用

【例2】　点(，2)与点分别在幂函数f(x)，g(x)的图象上，问当x为何值时，有：

(1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)<g(x)．

[解]　设f(x)＝xα，g(x)＝xβ.

∵()α＝2，(－2)β＝－，

∴α＝2，β＝－1，

∴f(x)＝x2，g(x)＝x－1．分别作出

它们的图象，如图所示．由图象知，

(1)当x∈(－∞，0)∪(1，＋∞)时，f(x)>g(x)；

(2)当x＝1时，f(x)＝g(x)；

(3)当x∈(0，1)时，f(x)<g(x)．

解决幂函数图象问题应把握的两个原则

(1)依据图象高低判断幂指数大小，相关结论为：在(0，1)上，指数越大，幂函数图象越靠近x轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图象越远离x轴(简记为指大图高)．

(2)依据图象确定幂指数α与0，1的大小关系，即根据幂函数在第一象限内的图象(类似于y＝x－1或y＝x或y＝x3)来判断．

2．(1)若四个幂函数y＝xa，y＝xb，y＝xc，y＝xd在同一坐标系中的图象如图，则a，b，c，d的大小关系是(　　)

A．d>c>b>a B．a>b>c>d

C．d>c>a>b D．a>b>d>c

(2)函数y＝x－1的图象关于x轴对称的图象大致是(　　)

A　　　　B　　　　　C　　　　D

(1)B　(2)B　[(1)令a＝2，b＝，c＝－，d＝－1，正好和题目所给的形式相符合．

在第一象限内，x＝1的右侧部分的图象，图象由下至上，幂指数增大，所以a>b>c>d.故选B．

(2)y＝x的图象位于第一象限且为增函数，所以函数图象是上升的，函数y＝x－1的图象可看作由y＝x的图象向下平移1个单位得到的(如选项A中的图所示)，将y＝x－1的图象关于x轴对称后即为选项B．]

类型3　幂函数性质的综合应用

【例3】　比较下列各组中幂值的大小：

(1)0.213，0.233；(2)1.2，0.9，.

由所给幂的特征，思考如何构造幂函数，幂函数的单调性如何？

[解]　(1)∵函数y＝x3是增函数，且0.21＜0.23，

∴0.213<0.233.

(2)0.9＝，＝1.1.

∵1.2>>1.1，且y＝x在[0，＋∞)上单调递增，

∴1.2>>1.1，即1.2>0.9>.

比较幂值大小的方法

(1)若两个幂值的指数相同或可化为两个指数相同的幂值时，则可构造函数，利用幂函数的单调性比较大小．

(2)若底数、指数均不同，则考虑用中间值法比较大小，这里的中间值可以是“0”或“1”．

3．比较下列各组数的大小：

(1)与；

(2)与.

[解]　(1)因为幂函数y＝x0.5在[0，＋∞)上是单调递增的，又>，所以>.

(2)因为幂函数y＝x－1在(－∞，0)上是单调递减的，

又－<－，

所以>.

1．幂函数的图象过点(2，)，则该幂函数的解析式是(　　)

A．y＝x－1 B．y＝x

C．y＝x2 D．y＝x3

B　[设f(x)＝xα，则2α＝，

∴α＝，∴f(x)＝x.故选B．]

2．已知函数f(x)＝(a2－a－1)x为幂函数，则实数a的值为(　　)

A．－1或2 B．－2或1

C．－1 D．1

C　[因为f(x)＝(a2－a－1)x为幂函数，所以a2－a－1＝1，即a＝2或－1．又a－2≠0，所以a＝－1．]

3．函数y＝x－3在区间[－4，－2]上的最小值是________．

－　[因为函数y＝x－3＝在(－∞，0)上单调递减，

所以当x＝－2时，y最小值＝(－2)－3＝＝－.]

4．0.23－2.3与0.24－2.3的大小关系是________．

0.23－2.3>0.24－2.3　[令y＝x－2.3，由于y＝x－2.3在(0，＋∞)上单调递减且0.23<0.24，故0.23－2.3>0.24－2.3.]

回顾本节知识，自我完成以下问题：

1．判断一个函数是幂函数的关键是什么？

[提示]　关键是判断其是否符合y＝xα(α为非零实数)的形式．

2．所有幂函数y＝xα在原点处都有意义吗？图象都过点(1，1)吗？

[提示]　当α<0时幂函数在原点处无意义，图象都过点(1，1)．

3．在第一象限内，幂函数图象随幂指数的变化存在怎样的规律？

[提示]　观察五种特殊的幂函数在第一象限内的图象，可知，幂函数y＝xα的图象在第一象限内具有如下特征：直线y＝1，y＝x将直角坐标平面的第一象限在直线x＝1的右侧部分分为(Ⅰ)(Ⅱ)(Ⅲ)三个区域，如图所示，若α∈(1，＋∞)⇔y＝xα的图象经过区域(Ⅰ)；若α∈(0，1)⇔y＝xα的图象经过区域(Ⅱ)；若α∈(－∞，0)⇔y＝xα的图象经过区域(Ⅲ)，并且在直线x＝1的右侧，从x轴起，幂函数y＝xα的指数α由小到大递增，即“指大图高”“指小图低”．