高中数学湘教版（2019）必修 第一册第4章 幂函数、指数函数和对数函数4.3 对数函数教课课件ppt

这是一份高中数学湘教版（2019）必修 第一册第4章 幂函数、指数函数和对数函数4.3 对数函数教课课件ppt，文件包含湘教版高中数学必修第一册第4章43432对数的运算法则课件ppt、湘教版高中数学必修第一册第4章43432对数的运算法则学案doc、湘教版高中数学必修第一册课后素养落实31对数的运算法则含答案doc等3份课件配套教学资源，其中PPT共48页， 欢迎下载使用。
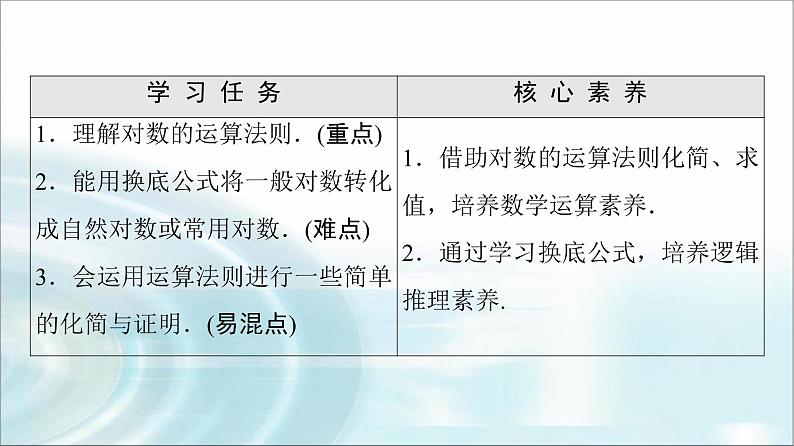
4.3.2　对数的运算法则学 习 任 务核 心 素 养1．理解对数的运算法则．(重点)2．能用换底公式将一般对数转化成自然对数或常用对数．(难点)3．会运用运算法则进行一些简单的化简与证明．(易混点)1．借助对数的运算法则化简、求值，培养数学运算素养．2．通过学习换底公式，培养逻辑推理素养.(1)计算log24，log28及log232的值，你能分析一下三者存在怎样的运算关系吗？(2)计算lg 10，lg 100，lg 1 000及lg 104的值，你能发现什么规律？知识点1　对数的运算法则如果a>0且a≠1，M>0，N>0，那么：(1)loga(M·N)＝logaM＋logaN；(2)logaMn＝nlogaM(n∈R)；(3)loga＝logaM－logaN.当M>0，N>0时，loga(M＋N)＝logaM＋logaN，loga(MN)＝logaM·logaN是否成立？[提示]　不一定．1．思考辨析(正确的打“√”，错误的打“×”)(1)log2x2＝2log2x.  (　　)(2)loga[(－2)×(－3)]＝loga(－2)＋loga(－3)． (　　)(3)logaM·logaN＝loga(M＋N)． (　　)[答案]　(1)×　(2)×　(3)×2.计算log84＋log82等于(　　)A．log86 B．8C．6 D．1D　[log84＋log82＝log88＝1．]3.计算log510－log52等于(　　)A．log58 B．lg 5C．1 D．2C　[log510－log52＝log55＝1．]知识点2　常用对数与自然对数4.(1)lg 100＝________，(2)ln ＝________.(1)2　(2)－1　[(1)lg 100＝lg 102＝2；(2)ln ＝ln e－1＝－1．]知识点3　对数的换底公式若b>0且b≠1，a>0且a≠1，N>0，则有logbN＝.几个常用推论：(1)loganbn＝logab(a>0，a≠1，b>0，n≠0)；(2)logambn＝logab(a>0，a≠1，b>0，m≠0，n∈R)；(3)logab·logba＝1(a>0，a≠1；b>0，b≠1)．5.(多选题)下列等式正确的有(　　)A．log34＝ B．log34＝C．log34＝ D．log34＝[答案]　ABC 类型1　对数的运算法则的应用【例1】　计算下列各式的值：(1)lg －lg ＋lg ；(2)lg 52＋lg 8＋lg 5·lg 20＋(lg 2)2；(3).[解]　(1)原式＝(5lg 2－2lg 7)－×lg 2＋(2lg 7＋lg 5)＝lg 2－lg 7－2lg 2＋lg 7＋lg 5＝lg 2＋lg 5＝(lg 2＋lg 5)＝lg 10＝.(2)原式＝2lg 5＋2lg 2＋lg 5(2lg 2＋lg 5)＋(lg 2)2＝2lg 10＋(lg 5＋lg 2)2＝2＋(lg 10)2＝2＋1＝3.(3)原式＝＝＝＝.1．利用对数运算法则求值的解题关键是化异为同，先使各项底数相同，再找真数间的联系．2．对于复杂的运算式，可先化简再计算．化简问题的常用方法：(1)“拆”：将积(商)的对数拆成两对数之和(差)；(2)“收”：将同底对数的和(差)收成积(商)的对数．1．求下列各式的值：(1)lg25＋lg 2·lg 50；(2)lg 8＋lg25＋lg 2·lg 50＋lg 25.[解]　(1)原式＝lg25＋(1－lg 5)(1＋lg 5)＝lg25＋1－lg25＝1．(2)lg 8＋lg25＋lg 2·lg 50＋lg 25＝2lg 2＋lg25＋lg 2(1＋lg 5)＋2lg 5＝2(lg 2＋lg 5)＋lg2 5＋lg 2＋lg 2·lg 5＝2＋lg 5(lg 5＋lg 2)＋lg 2＝2＋lg 5＋lg 2＝3. 类型2　对数的换底公式【例2】　(1)计算：(log2125＋log425＋log85)·(log1258＋log254＋log52)；(2)已知log189＝a,18b＝5，求log3645(用a，b表示)．[解]　(1)(log2125＋log425＋log85)·(log1258＋log254＋log52)＝(log253＋log2252＋log235)·(log5323＋log5222＋log52)＝log25·(1＋1＋1)log52＝·3＝13.(2)∵18b＝5，∴b＝log185.又log189＝a，∴log3645＝＝＝＝.(变结论)在本例(2)的条件下，求log915(用a，b表示)．[解]　∵log189＝a，∴log183＝.又log185＝b，∴log915＝＝＝＝.利用换底公式进行化简求值的原则和技巧2．求值：(1)log23·log35·log516；(2)(log32＋log92)(log43＋log83)．[解]　(1)原式＝··＝＝＝4.(2)原式＝＝＝·＝. 类型3　对数的运算法则的综合应用【例3】　(1)若3x＝4y＝36，求＋的值；(2)已知3x＝4y＝6z，求证：＋＝.以指数式与对数式间的内在联系为切入点，思考如何求解相应问题.[解]　(1)∵3x＝4y＝36，∴x＝log336，y＝log436.∴＝＝＝2log363＝log369，＝＝＝log364.∴＋＝log369＋log364＝log3636＝1．(2)证明：设3x＝4y＝6z＝m(m>0)，则x＝log3m，y＝log4m，z＝log6m.所以＝＝logm3，＝＝logm4，＝＝logm6.故＋＝logm3＋logm4＝logm3＋logm4＝logm3＋logm2＝logm(3×2)＝logm6＝.条件求值问题的求解方法带有附加条件的代数式求值问题，需要对已知条件和所求式子进行化简转化，原则上是化为同底的对数，以便 利用对数的运算法则．要整体把握对数式的结构特征，灵活运用指数式与对数式互化进行解题．3．已知3a＝5b＝c，且＋＝2，求c的值．[解]　∵3a＝5b＝c，∴a＝log3c，b＝log5c，∴＝logc3，＝logc5，∴＋＝logc15.由logc15＝2得c2＝15，即c＝.1.2log510＋log50.25＝(　　)A．0　 B．1　　　　C．2　　　　 D．4C　[∵2log510＋log50.25＝log5100＋log50.25＝log525＝2.∴选C．]2．计算log92·log43＝(　　)A．4 B．2C． D．D　[log92·log43＝·＝·＝.]3．设10a＝2，lg 3＝b，则log26＝(　　)A． B．C．ab D．a＋bB　[∵10a＝2，∴lg 2＝a，∴log26＝＝＝.]4．若a>0，a≠1，x>0，n∈N＋，则下列各式：(1)(logax)n＝nlogax；(2)(logax)n＝logaxn；(3)logax＝－loga；(4)＝logax；(5)＝loga.其中正确的有________．(填序号)(3)(5)　[根据对数的运算法则logaMn＝nlogaM(M>0，a>0，且a≠1)知(3)与(5)正确．]5．已知2a＝5b＝10，则＋＝________.1　[∵2a＝5b＝10，∴a＝log210，b＝log510，∴＝log102＝lg 2，＝lg 5，∴＋＝lg 2＋lg 5＝lg 10＝1．]回顾本节知识，自我完成以下问题：1．对数的运算法则有哪些？[提示]　(1)loga(M·N)＝logaM＋logaN；(2)loga＝logaM－logaN；(3)logaMn＝nlogaM.其中(a>0且a≠1，M>0，N>0)2．你能用对数的换底公式证明logNnMm＝logNM吗？[提示]　能．logNnMm＝＝＝logNM.3．常见的换底公式变形有哪些？[提示]　(1)logab＝＝＝(其中a>0，b>0，c>0且a≠1，c≠1)．(2)logab·logba＝1(其中a>0且a≠1，b>0且b≠1)．