高中湘教版（2019）6.4 用样本估计总体评课课件ppt

6.4.4　百分位数

知识点　百分位数

1．定义

百分位数是位于按一定顺序排列的一组数据中某一个百分位置的数值，以Pr表示，其中r是区间[1,99]上的整数．一个百分位数Pr将总体或样本的全部观测值分为两部分，至少有r%的观测值小于或等于它，且至少有(100－r)%的观测值大于或等于它，当r%＝50%时，Pr即对应中位数．

2．计算一组n个数据的第P百分位数的步骤

第1步，按从小到大排列原始数据．

第2步，计算c＝n×r%.

第3步，若c不是整数，用m表示比c大的最小整数，则所求Pr是xm，如果c是整数，则所求的Pr是.

3．四分位数

25%,50%,75%这三个分位数把一组由小到大排列后的数据分成四等份，因此称为四分位数．

(1) 班级人数为50的班主任老师说“90%的同学能够考取本科院校”，这里的“90%”是百分位数吗？

(2)“这次数学测试成绩的第70百分位数是85分”这句话是什么意思？

[提示]　(1)不是．是指能够考取本科院校的同学占同学总数的百分比．

(2)有70%的同学数学测试成绩小于或等于85分．

1．思考辨析(正确的打“√”，错误的打“×”)

(1)若一组样本数据各不相等，则其75%分位数大于25%分位数． (　　)

(2)若一组样本数据的10%分位数是23，则在这组数据中有10%的数据大于23.               (　　)

(3)若一组样本数据的24%分位数是24，则在这组数据中至少有76%的数据大于或等于24.               (　　)

[答案]　(1)√　(2)×　(3)√

2.下列关于一组数据的第50百分位数的说法正确的是(　　)

A．第50百分位数就是中位数

B．总体数据中的任意一个数小于它的可能性一定是50%

C．它一定是这组数据中的一个数据

D．它适用于总体是离散型的数据

A　[由百分位数的意义可知选项B，C，D错误．]

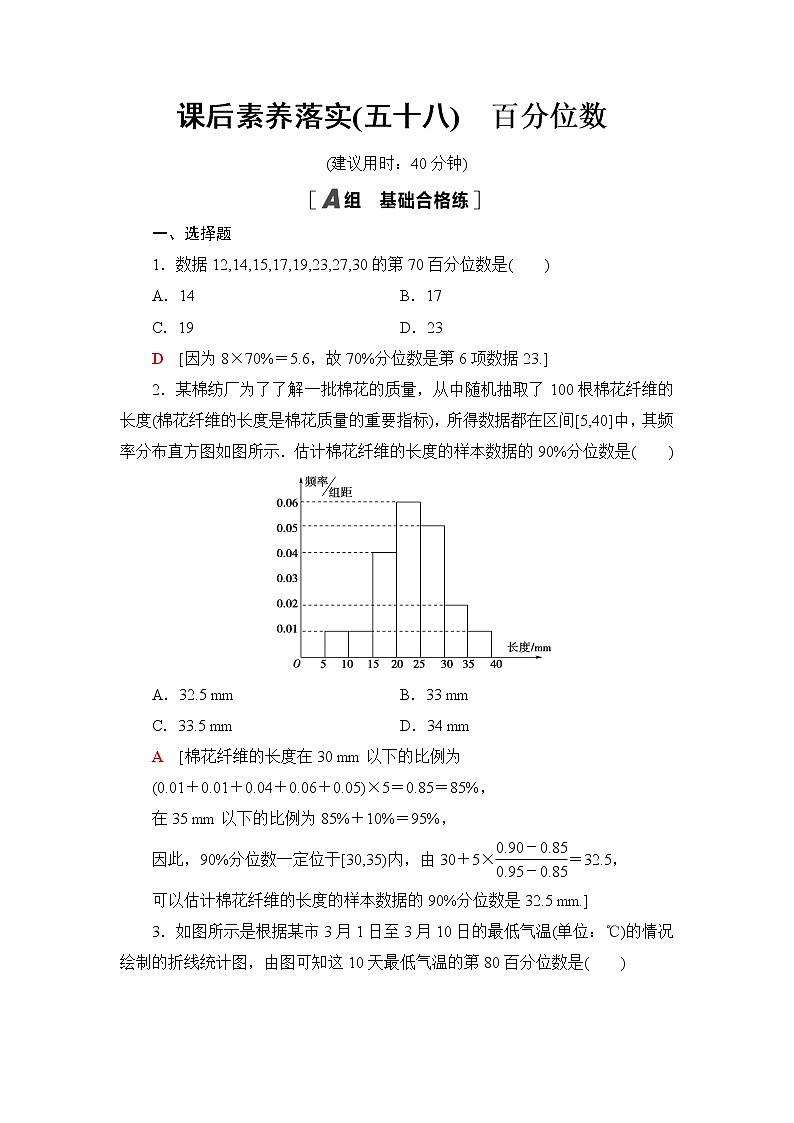
3.数据7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1的第30百分位数是________．

8.4　[因为8×30%＝2.4，故30%分位数是第三项数据8.4.]

4.一组样本数据的频率分布直方图如图所示，试估计此样本数据的第50百分位数为________．

　[样本数据低于10的比例为0.08 ＋0.32＝0.40，样本数据低于14的比例为0.40 ＋0.36＝0.76，所以此样本数据的第50百分位数在[10,14]内，估计此样本数据的第50百分位数为10＋×4＝.]

类型1　百分位数的计算

【例1】　从某珍珠公司生产的产品中，任意抽取12颗珍珠，得到它们的质量(单位：g)如下：

79,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0.

(1)分别求出这组数据的第25,75,95百分位数．

(2)请你找出珍珠质量较小的前15%的珍珠质量．

(3)若用第25,50,95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品，依照这个样本的数据，给出该公司珍珠等级的划分标准．

[解]　(1)将所有数据从小到大排列，得

7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9，

因为共有12个数据，所以12×25%＝3,12×75%＝9,12×95%＝11.4，

则第25百分位数是＝8.15，

第75百分位数是＝8.75，

第95百分位数是第12个数据为9.9.

(2)因为共有12个数据，所以12×15%＝1.8，则第15百分位数是第2个数据为7.9.

即产品质量较小的前15%的产品有2个，它们的质量分别为7.8,7.9.

(3)由(1)可知样本数据的第25百分位数是8.15 g，第50百分位数为8.5 g, 第95百分位数是9.9 g，所以质量小于或等于8.15 g的珍珠为次品，质量大于8.15 g且小于或等于8.5 g的珍珠为合格品，质量大于8.5 g且小于等于9.9 g的珍珠为优等品，质量大于9.9 g的珍珠为特优品．

计算第P百分位数的步骤

(1)排列：按照从小到大排列原始数据；

(2)计算c：计算c＝n×r%；

(3)定数：若c不是整数，大于c的最小整数为m，则第P百分位数为第m项数据；若c整数，则第P百分位数为第m项与第(c＋1)项数据的平均数．

1．以下数据为参加数学竞赛决赛的15人的成绩：

78,70,72,86,88,79,80,81,94,84,56,98,83,90,91，

则这15人成绩的第80百分位数是(　　 )

A．90 B．90.5　　　

C．91　　　 D．91.5

B　[把成绩按从小到大的顺序排列为：

56,70,72,78,79,80,81,83,84,86,88,90,91,94,98，

因为15×80%＝12，所以这15人成绩的第80百分位数是＝90.5.]

类型2　百分位数的综合应用

【例2】　某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200千瓦时的部分按0.5元/千瓦时收费，超过200千瓦时但不超过400千瓦时的部分按0.8元/千瓦时收费，超过400千瓦时的部分按1.0元/千瓦时收费．

(1)求某户居民用电费用y(单位：元)关于月用电量x(单位：千瓦时)的函数解析式．

(2)为了了解居民的用电情况，通过抽样获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图．若这100户居民中，今年1月份用电费用不超过260元的占80%，求a，b的值．

(3)根据(2)中求得的数据计算用电量的75%分位数．

(1)第P百分位数有什么特点？

(2)某组数据的第P百分位数在此组数据中一定存在吗？为什么？

[解]　(1)当0≤x≤200时，y＝0.5x；

当200<x≤400时，y＝0.5×200＋0.8×(x－200)＝0.8x－60；

当x>400时，y＝0.5×200＋0.8×200＋1.0×(x－400)＝x－140.

所以y与x之间的函数解析式为

y＝

(2)由(1)可知，当y＝260时，x＝400，即用电量不超过400千瓦时的占80%，

结合频率分布直方图可知

解得a＝0.001 5，b＝0.002 0.

(3)设75%分位数为m，

因为用电量低于300千瓦时的所占比例为(0.001＋0.002＋0.003)×100＝60%，

用电量不超过400千瓦时的占80%，

所以75%分位数为m在[300,400)内，所以0.6＋(m－300)×0.002＝0.75，

解得m＝375千瓦时，

即用电量的75%分位数为375千瓦时．

根据频率分布直方图计算样本数据的百分位数，首先要理解频率分布直方图中各组数据频率的计算，其次估计百分位数在哪一组，再应用方程的思想方法，设出百分位数，解方程可得.

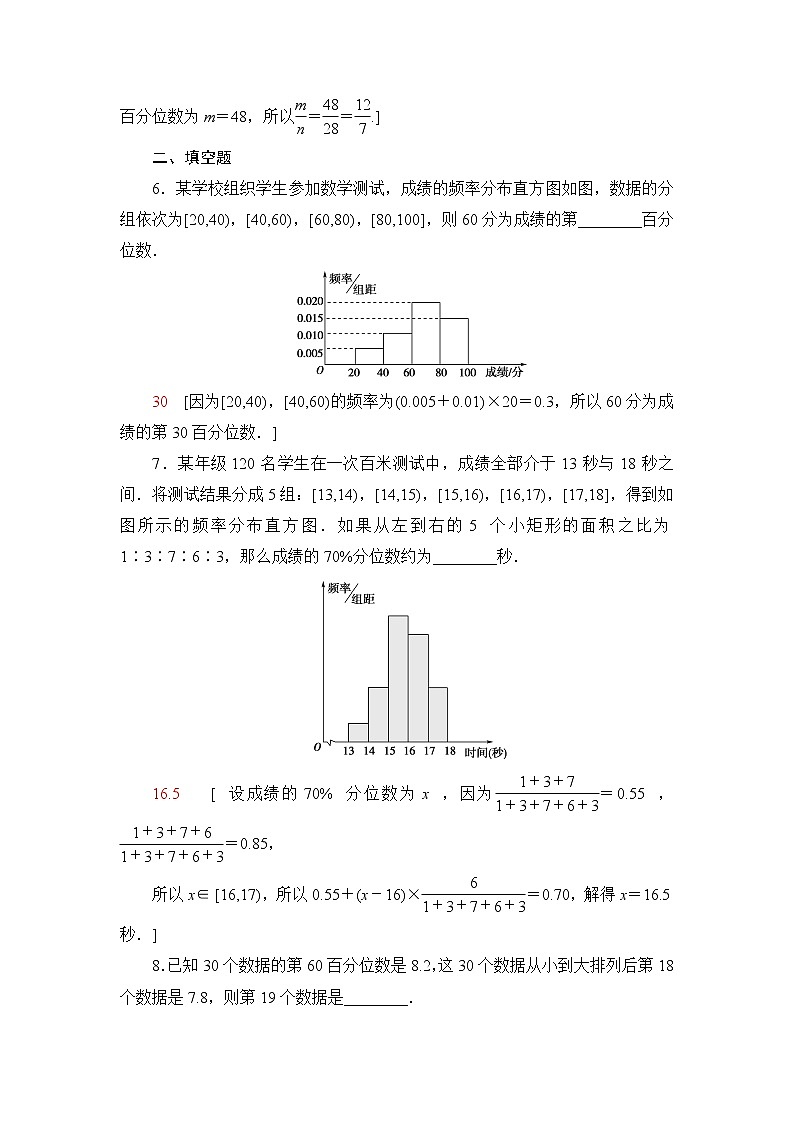
2．某市举行“中学生诗词大赛”，某校有1 000名学生参加了比赛，从中抽取100名学生，统计他们的成绩(单位：分)，并进行适当的分组(每组为左闭右开的区间)，得到的频率分布直方图如图所示，则估计该校学生成绩的80%分位数为________．

122　[根据频率分布直方图可知，成绩在130分以下的学生所占比例为1－0.005 0×20＝0.9，成绩在110分以下的学生所占比例为1－(0.012 5＋0.005 0)×20＝0.65，因此80%分位数一定位于[110,130)内，由110＋20×＝122，故可估计该校学生成绩的80%分位数为122.]

1．下列一组数据的第25百分位数是(　　)

2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6

A．3.2 B．3.0　　　

C．4.4　　　 D．2.5

A　[把这组数据按照由小到大排列，可得：

2.1,3.0,3.2,3.4,3.8, 4.0,4.2,4.4,5.3,5.6，

由c＝10×25%＝2.5，不是整数，则第3个数据3.2是第25百分位数．]

2．已知100个数据的第75百分位数是9.3，则下列说法正确的是(　　)

A．这100个数据中一定有75个数小于或等于9.3

B．把这100个数据从小到大排列后，9.3是第75个数据

C．把这100个数据从小到大排列后，9.3是第75个数据和第76个数据的平均数

D．把这100个数据从小到大排列后，9.3是第75个数据和第74个数据的平均数

C　[因为100×75%＝75为整数，所以第75个数据和第76个数据的平均数为第75百分位数，是9.3，故选C．]

3．2020年某学科能力测试共有12万考生参加，成绩采用15级分，测试成绩分布图如图，试估计成绩高于11级分的人数为(　　)

A．8 000　　 B．10 000

C．20 000　　 D．60 000

B　[从题图中可以看出，12级分的有2.5%左右，13级分的有3%左右，14级分的有1%左右，15级分的有1.5%左右，

∴高于11级分的有8%左右，其人数约为12万的8%，即120 000×0.08＝9 600人．选项B最接近．故选B．]

4．对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图)，但是年龄组为[25,30)的数据不慎丢失，则依据此图可得：

(1)[25,30)年龄组对应小矩形的高度为________；

(2)由频率分布直方图估计志愿者年龄的95%分位数为________岁．

(1)0.04　(2)42.5　[(1)设[25,30)年龄组对应小矩形的高度为h，则5×(0.01＋h＋0.07＋0.06＋0.02)＝1，解得h＝0.04.

(2)由题图可知年龄小于40岁的频率为(0.01＋0.04＋0.07＋0.06)×5＝0.9，

且所有志愿者的年龄都小于45岁，所以志愿者年龄的95%分位数在[40,45]内，

因此志愿者年龄的95%分位数为40＋×5＝42.5岁．]

回顾本节知识，自我完成以下问题：

1．P百分位数有什么特点？

[提示]　总体数据中的任意一个数小于或等于它的可能性是P%.

2．如何求一组数据的P百分位数？

[提示]　求一组数据的百分位数时其步骤：①按照从小到大排列原始数据；②计算i＝P×p%；③若i不是整数，大于i的最小整数为j，则P百分位数为第j项数据；若i是整数，则P百分位数为i项与第(i＋1)项数据的平均数．