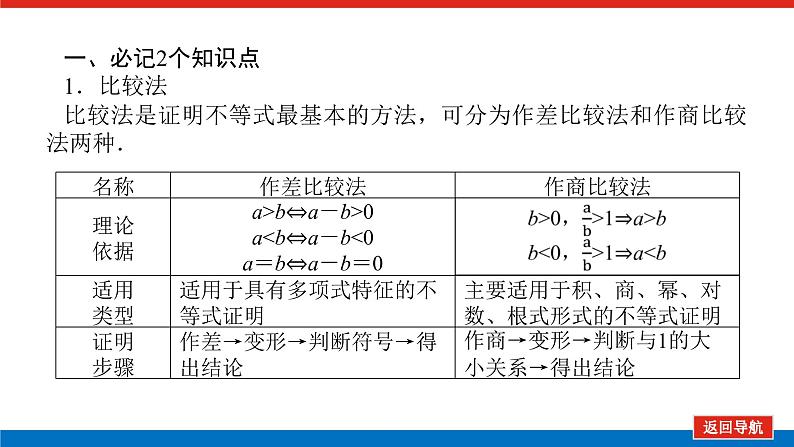
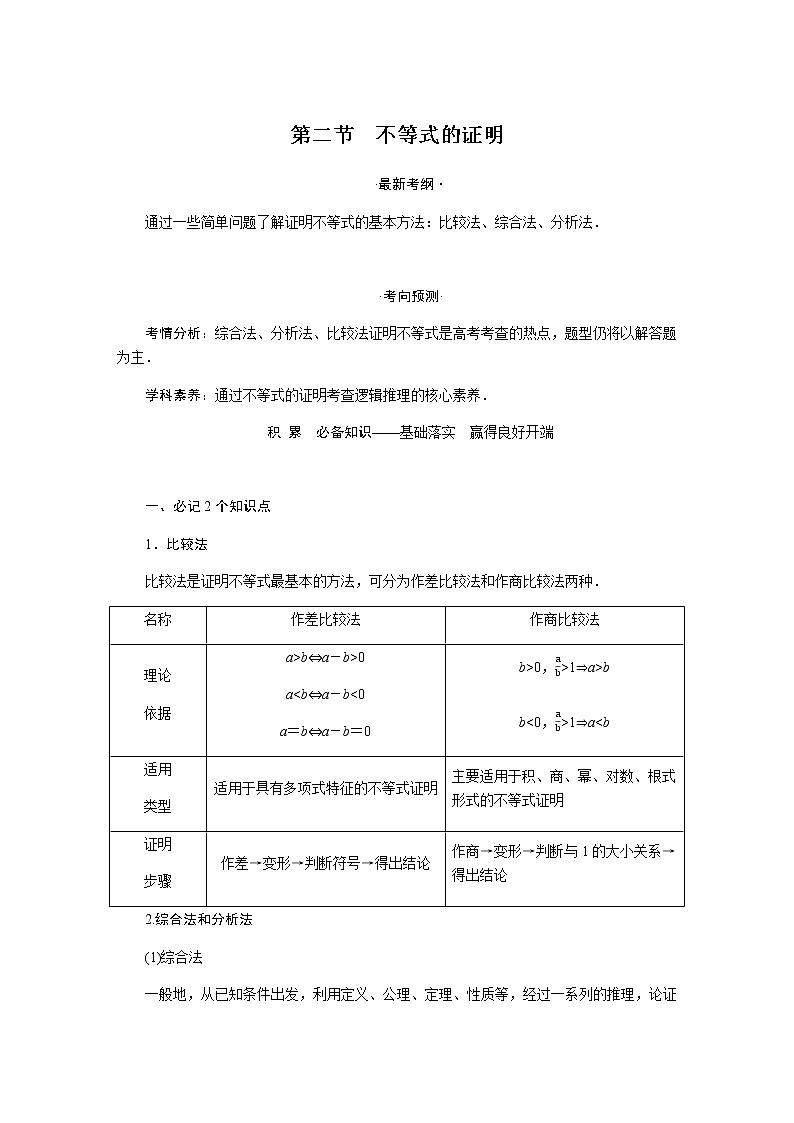
统考版高中数学（理）一轮复习选修4－5不等式选讲导学案+PPT课件

这是一份统考版高中数学（理）一轮复习选修4－5不等式选讲导学案+PPT课件，文件包含选4-51pptx、选4-52pptx、选4-51docx、选4-52DOCX等4份课件配套教学资源，其中PPT共42页， 欢迎下载使用。

·最新考纲·1．理解绝对值的几何意义，并了解下列不等式成立的几何意义及取等号的条件：|a＋b|≤|a|＋|b|；|a－b|≤|a－c|＋|c－b|.2．会利用绝对值的几何意义求解以下类型的不等式：|ax＋b|≤c；|ax＋b|≥c；|x－a|＋|x－b|≥c.
·考向预测·考情分析：绝对值不等式的解法，绝对值不等式的性质，与绝对值相关的参数问题，将是高考考查的热点，题型仍将是解答题．学科素养：通过绝对值不等式的求解及绝对值不等式性质的应用考查数学运算、逻辑推理的核心素养．
一、必记2个知识点1．含有绝对值的不等式定理(1)定理：对任意实数a和b，有__________________，其中等号成立的条件为ab≥0.(2)定理中的b以－b代替，则有|a－b|≤|a|＋|b|.其中等号成立的条件为_________．(3)对任意实数a和b，有||a|－|b||≤|a±b|≤|a|＋|b|.
|a＋b|≤|a|＋|b|
2．绝对值不等式的解法(1)含绝对值的不等式|x|＜a与|x|＞a的解集：
{x|x＞a或x＜－a}
{x|x∈R且x≠0}
(2)|ax＋b|≤c(c＞0)和|ax＋b|≥c(c＞0)型不等式的解法：①|ax＋b|≤c⇔－c≤ax＋b≤c；②|ax＋b|≥c⇔ax＋b≥c或ax＋b≤－c.(3)|x－a|＋|x－b|≥c(c＞0)和|x－a|＋|x－b|≤c(c＞0)型不等式的解法．①利用绝对值不等式的几何意义求解，体现了数形结合的思想．②利用“零点分段法”求解，体现了分类讨论的思想．③通过构造函数，利用函数的图象求解，体现了函数与方程的思想．
二、必明3个常用结论1．绝对值不等式的性质||a|－|b||≤|a－b|≤|a|＋|b|，等号成立的条件：当ab≥0时，左侧不等式成立；当ab≤0时，右侧不等式成立．2．两个等价关系(1)|x|0)⇔－aa(a>0)⇔x<－a或x>a.推广：①|x|f(x)⇔x<－f(x)或x>f(x)．3．实用口诀解含绝对值的不等式：“找零点，分区间，逐个解，并起来．”
考点一　含绝对值不等式的解法　[基础性、应用性]  [例1]　[2021·全国甲卷]已知函数f(x)＝|x－2|，g(x)＝|2x＋3|－|2x－1|. (1)画出y＝f(x)和y＝g(x)的图象；
(2)若f(x＋a)≥g(x)，求a的取值范围．
反思感悟　解绝对值不等式的基本方法
【对点训练】[2020·全国卷Ⅰ]已知函数f(x)＝|3x＋1|－2|x－1|.(1)画出y＝f(x)的图象；  
(2)求不等式f(x)>f(x＋1)的解集．
反思感悟　对绝对值三角不等式定理的理解注意以下三点(1)等号成立的条件在解题时经常用到，特别是用此定理求函数的最大(小)值时．(2)该定理可推广为|a＋b＋c|≤|a|＋|b|＋|c|，也可强化为||a|－|b||≤|a±b|≤|a|＋|b|，它们经常用于含绝对值的不等式的推论．(3)当ab≥0时，|a＋b|＝|a|＋|b|；当ab≤0时，|a－b|＝|a|＋|b|；当b(a＋b)≤0时，|a|－|b|＝|a＋b|；当b(a－b)≥0时，|a|－|b|＝|a－b|.
考点三　绝对值不等式的综合应用　[应用性、创新性]  [例3]　[2022·惠州市高三调研考试]已知f(x)＝|x＋1|＋|ax－a＋1|.(1)当a＝1时，求不等式f(x)≥3的解集；(2)若x≥1时，不等式f(x)≥x＋2恒成立，求a的取值范围．
【对点训练】1．[2021·全国乙卷]已知函数f(x)＝|x－a|＋|x＋3|.(1)当a＝1时，求不等式f(x)≥6的解集；(2)若f(x)>－a，求a的取值范围．
2．设函数f(x)＝|2x＋3|＋|x－1|.(1)解不等式f(x)>4；