线性规划题型方法 讲义——高考数学一轮复习

这是一份线性规划题型方法 讲义——高考数学一轮复习，共9页。
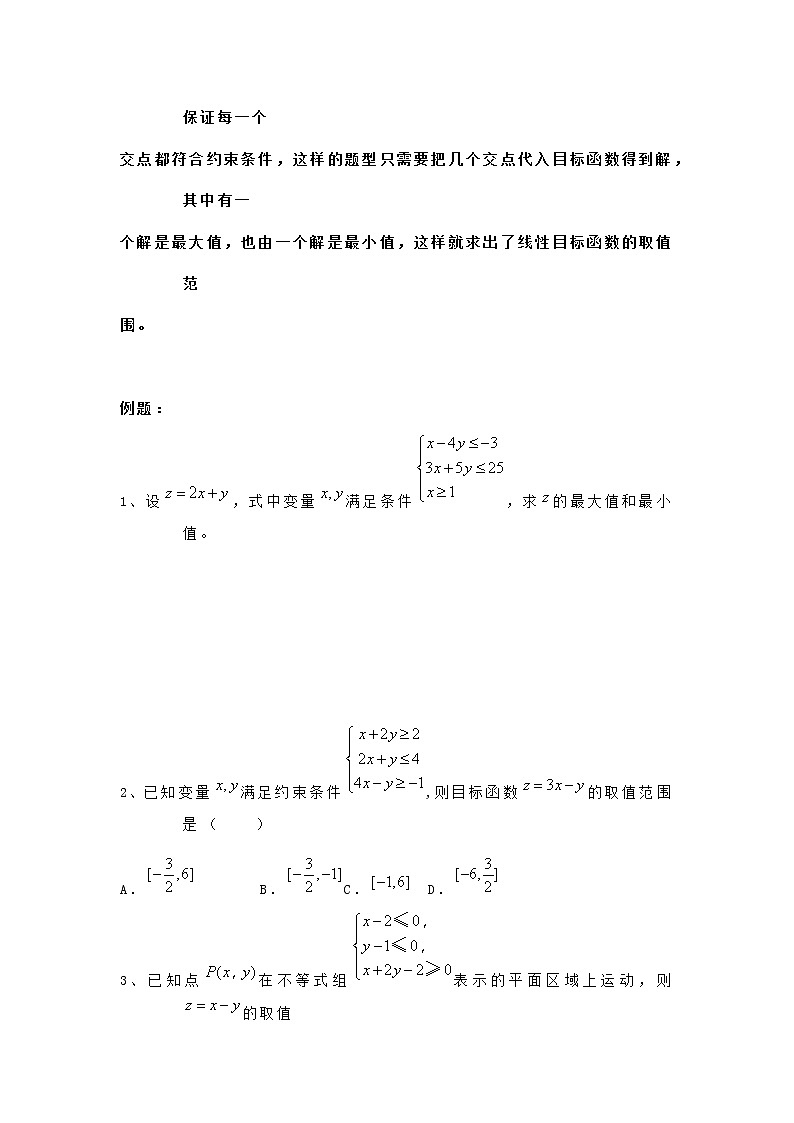
线性规划的常见题型及解法知识点复习：1 二元一次不等式（组）表示的平面区域（1）对于不含边界的区域，要将边界画成虚线。（2）直线把平面内不在直线上的点分成两部分，对于同一侧所有点的坐标代入中所得的值的符号都相同，异侧所有点的坐标代入所得的值的符号都相反。（3）对于直线当时，可化为：的形式.对于二元一次不等式表示的平面区域在直线的上方（包括直线）.对于二元一次不等式表示的平面区域在直线的下方（包括直线）。2 线性规划（1）线性约束条件：在上述问题中，不等式组是一组变量的约束条件，这组约束条件都是关于的一次不等式，故又称线性约束条件．（2）线性目标函数：关于的一次式是欲达到最大值或最小值所涉及的变量的解析式，叫线性目标函数．（3）线性规划问题：一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题．（4）可行解：满足线性约束条件的解叫可行解。（5）可行域由所有可行解组成的集合叫做可行域。（6）最优解：使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。3我们把求线性目标函数在线性目标条件下的最值问题称为线性规划问题.解决这类问题的基本步骤是：（1）确定好线性约束条件，准确画出可行域.（2）对目标函数，若，则取得最大值（或最小值）时，也取得最大值（或最小值）；若，则反之.（3）一般地，可行域是凸多边形顶点有可能是最值点，有些问题可直接代入边缘点找最值.（4）注意实际问题中的特殊要求. 注意：可行区域的判断和确定，以及开放型区域和封闭式区域的确定；最优解的确定，最优解一定在可行区域的边界上，目标函数的三种模型，或（）根据目标函数的几何意义，确定最优解。         常考题型： 题型一：求线性目标函数的最值方法：首先确保可行域是封闭区域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件，这样的题型只需要把几个交点代入目标函数得到解，其中有一个解是最大值，也由一个解是最小值，这样就求出了线性目标函数的取值范围。 例题：1、设，式中变量满足条件，求的最大值和最小值。    2、已知变量满足约束条件,则目标函数的取值范围是 （　　）A．      B． C． D．3、已知点在不等式组表示的平面区域上运动，则的取值范围是（　　）．（A）　　（B）  （C）　　  （D）  题型二：求可行域的面积方法：首先确保可行域是封闭区域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件，这样的题型得到的可行域是多边形，根据多边形的特点，求可行域的面积。 例题：1、不等式组表示的平面区域的面积为　　（　）A、4　B、1　C、5　D、无穷大2、在平面直角坐标系中，不等式组表示的平面区域的面积是（     ） (A)        (B)4          (C)              (D)2   题型三 ：求线性目标函数中参数的取值范围方法：首先确保可行域是封闭区域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件，这样的题型关键是看目标函数的特点，目标函数重点求什么，先将目标函数成一次函数的形式，然后平移得出相应的结论。 例题：1、已知变量，满足约束条件，若目标函数（其中）仅在点处取得最大值，则的取值范围为               .2、已知满足以下约束条件，使取得最小值的最优解有无数个，则的值为　（　）A、－3　B、3　C、－1　D、1 题型四： 约束条件中含参数的问题方法：这种题型确定可行域的时候，有的直线是未知的，可通过目标函数的最值来确定约束条件未知的直线，从而求出参数的具体值。当然有的题型有所不同，需要根据具体问题具体分析。 例题：1、已知＞0， 满足约束条件， 若的最小值是1，则＝（     ）（A）         （B）      （C）1         （D）22、关于的不等式组表示的平面区域内存在点满足，求得的取值范围是A.     B.    C.    D.  3、在约束条件下，当时，目标函数的最大值的变化范围是（   ）    A.    B.      C.      D.      题型五：目标函数是直线斜率的问题方法：首先确定可行域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件，然后构造目标函数的直线斜率的表达式，然后可行域的交点，来确定直线斜率的大小。 例题：1、在平面直角坐标系中，为不等式组所表示的区域上一动点，则直线 的斜率的最小值为(A)  2          (B)  1           (C)           (D)  2、已知变量满足约束条件，则 的取值范围是（    ）.（A）       （B）     （C）        （D）  题型六：求非线性目标函数的最值问题方法：首先确定可行域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件，然后构造目标函数的特点，需要根据具体问题具体分析。 例题：1、已知满足以下约束条件　，则的最大值和最小值分别是（　）　　A 13，1　   B  13，2　C  13，　   D、，3、已知则的最小值是        .  题型七：可行域中的整数问题（不包括边界问题）方法：首先确定可行域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件，根据可行域的特点，来确定可行域的整数个数。如果不包括边界问题，就是在可行域中不包括边界点。 例题：1、满足的点中整点（横纵坐标都是整数）有（　）A、9个　B、10个　C、13个　D、14个2、画出不等式组表示的平面区域，并回答下列问题：(1)指出x，y的取值范围；(2)平面区域内有多少个整点？  题型八：线性规划的综合问题这种题型包括很多种形式，需要具体的问题具体研究，但是共同点是首先确定可行域，那么首先求出可行域的几个交点，且保证每一个交点都符合约束条件。有的时候出现自己构造目标函数的题型，还有目标函数需要移动的题型，需要我们整理。例题：1、已知平面直角坐标系xOy上的区域D由不等式组给定，若M(x，y)为D上的动点，点A的坐标为(，1)，则z＝·的最大值为(　　)A．4   B．3  C．4   D．32、设D是不等式组所表示的平面区域，则区域D中的点P(x，y)到直线x＋y＝10的距离的最大值是________．3、若直线y＝kx＋1与圆x2＋y2＋kx＋my－4＝0相交于P、Q两点，且点P、Q关于直线x＋y＝0对称，则不等式组表示的平面区域的面积是(　　)A.　　　　B.　　　　C．1　　　　D．2