中职数学高教版（2021）基础模块上册3.3 函数的性质教学设计

这是一份中职数学高教版（2021）基础模块上册3.3 函数的性质教学设计
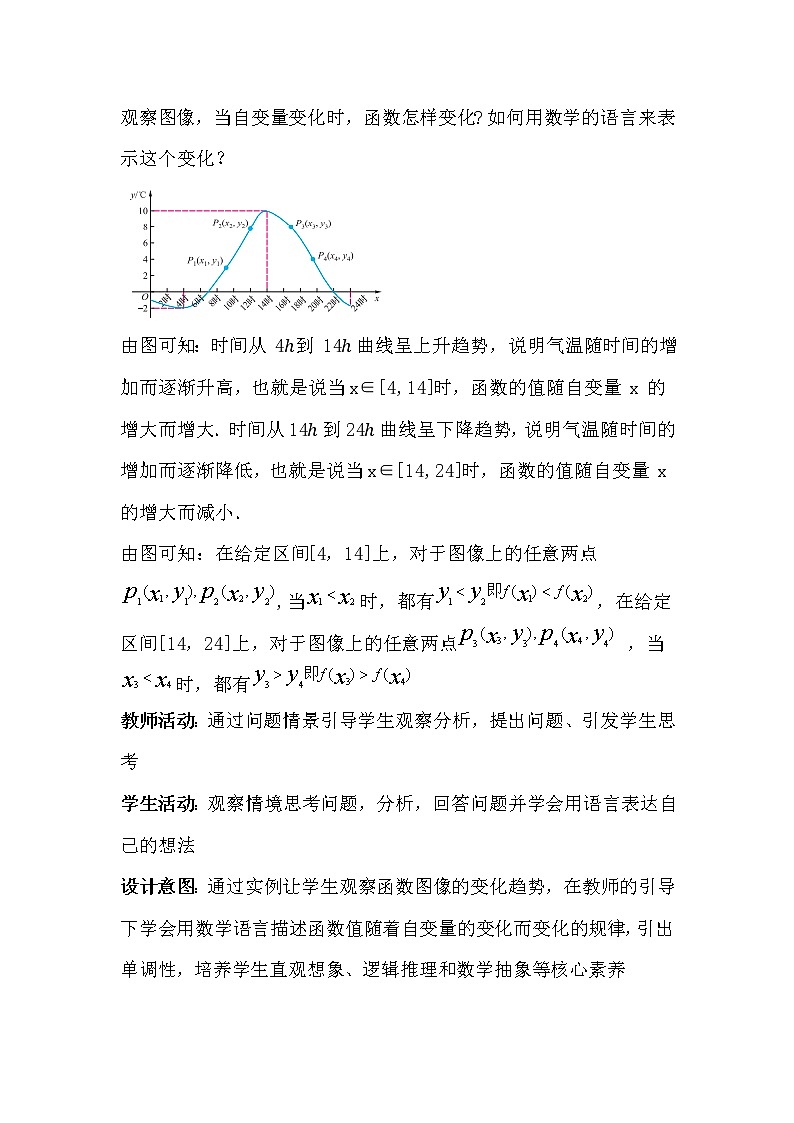
《函数的性质》教案授课题目：3.3函数的性质选用教材：高等教育出版社《数学》（基础模块上册）授课时长：4课时授课类型：新授课教学目标：结合函数图像，能用数学语言表达函数单调性、奇偶性的定义，能通过图像法和定义法判断函数的单调性和奇偶性，逐步提高直观想象和数学抽象等核心素养；能利用函数的单调性判断同一单调区间内两个函数值的大小，知道函数奇偶性与函数图像对称性之间的关系，能从函数单调性、奇偶性等角度，重新认识一次函数、反比例函数和一元二次函数，初步学会在具体函数中怎样研究对函数的一般性质的方法，逐步提高数学抽象、逻辑推理等核心素养．教学重点：函数的单调性和奇偶性及几种常见函数的性质教学难点：定义法判断函数单调性和奇偶性教学过程：1、情境引入函数是描述客观事物运动变化规律的数学模型．了解了函数的变化规律，也就基本把握了相应事物的变化规律，因此这一节我们一起来研究函数的性质． 3.3.1 函数的单调性 请大家观察下图，这是某市某天气温y（℃）是时间x（时）的函数图像，记这个函数为y=f(x)． 观察图像，当自变量变化时，函数怎样变化? 如何用数学的语言来表示这个变化？由图可知：时间从 4ℎ到 14ℎ曲线呈上升趋势，说明气温随时间的增加而逐渐升高，也就是说当x∈[4,14]时，函数的值随自变量 x 的增大而增大．时间从 14ℎ到 24ℎ曲线呈下降趋势，说明气温随时间的增加而逐渐降低，也就是说当x∈[14,24]时，函数的值随自变量 x 的增大而减小． 由图可知：在给定区间[4，14]上，对于图像上的任意两点,当时，都有，在给定区间[14，24]上，对于图像上的任意两点 ，当时，都有教师活动：通过问题情景引导学生观察分析，提出问题、引发学生思考学生活动：观察情境思考问题，分析，回答问题并学会用语言表达自己的想法设计意图：通过实例让学生观察函数图像的变化趋势，在教师的引导下学会用数学语言描述函数值随着自变量的变化而变化的规律，引出单调性，培养学生直观想象、逻辑推理和数学抽象等核心素养探索新知从上述例子可抽象出如下定义：设函数y=f(x)的定义域为 D，区间I∈D． （1）如果对于区间I上的任意两点x1 ,x2,当时，都有 ,那么称函数y=f(x)在区间上是增函数，区间I称为函数y=f(x)的增区间．如图（1）所示．（2）如果对于区间上的任意两点x1 ,x2，当时，都有 ,那么称函数y=(x)在区间上是减函数，区间I称为函数y=f(x)的减区间．如图（2）所示．如果函数y=f(x)在区间I上是增函数或减函数，那么称函数y=f(x)在区间I上具有单调性，区间I称为单调区间．增区间也称为单调增区间，减区间也称为单调减区间．教师活动：归纳总结定义，带领学生仔细分析具体情况，讲解关键词，并带领学生观察图像学生活动：观察情境思考问题，分析，回答问题并学会用语言表达自己的想法设计意图：师生共同归纳函数的单调性的定义，学会定性描述和定量刻画函数的单调性，培养学生数学抽象等核心素养例题分析例 1 根据函数在 R 上的图像，如图所示，写出其单调区间：解 （1）由图（1）所示函数图像可知，函数y=f(x)的定义域为R，增区间为(−∞， 0]，减区间为[0，+∞)．由函数图像（2）可知，函数y=g(x)的定义域为(−∞， 0)∪（0,+∞)，增区间为(−∞， 0)和（0,+∞)．探究与发现函数的减区间能写成(−∞， 0)∪(0,+∞)吗？例2 讨论函数f(x)=2x+1在(−∞，+∞）上的单调性．证:任取x1,x2∈(−∞，+∞)且x10,x1x2>0，所以f(x1)−f(x2)>0，即f(x1)>f(x2)．所以函数f(x)=2x+7在(−∞，+∞）上是增函数．例3证明函数f(x)=1/x+1在区间(−∞， 0)上是减函数．证:任取x1,x2∈(−∞， 0)且x10,x1x2>0，所以f(x1)−f(x2)>0，即f(x1)>f(x2)．所以函数f(x)=1/x+1在区间(−∞， 0) 上是减函数．教师活动：教师巡视指导，并对学生的回答给予指导学生活动：认真思考并答题设计意图：通过例题帮助学生理解函数的单调性，并学会利用图像法和定义法判断函数的单调性，在解决问题时强调学生注意给定区间4、巩固练习1．填空题（填“增”或“减”）：（1）函数y=x+1在（－∞，+∞）上是_________函数；（2）函数y=－2x 在（－∞，+∞）上是_________函数；（3）函数y=2/x 在（－∞，0）上是_________函数；（4）函数y=−5/x 在（0，+∞）上是_________函数；2．已知函数y=f(x)，x∈[−2,4]，如图所示，试写出函数的单调区间，并说明在每一单调区间上函数的单调性．3． 若函数f(x)=mx+2x−5在R上是减函数，求m的取值范围．4．证明：（1）函数f(x)=−x−2在(−∞,+∞)上是减函数． （2）函数f(x)=2x^2+1在(−∞,0)上是减函数．教师活动：提问 、巡视指导、及时指出学生的问题 学生活动：思考问题、动手做题求解答案、与小组同学交流 设计意图：通过练习及时掌握学生的知识掌握情况，查漏补缺3.3.2 函数的奇偶性1、情境引入大千世界，美无处不在．下图展示了生活中的对称之美． 其实，我们的数学中也存在着对称美，函数图像的对称就是其中一种．义务教育阶段，我们已经知道函数的图像和的图像： 函数的图像是关于轴对称的轴对称图形，函数的图像是关于原点对称的中心对称图形．观察这两种对称的函数图像，自变量互为相反数时，它们对应的函数值有什么关系？ 关于函数的图像分析：从函数值的角度看，对于函数 ， 有：f(−1)=1=f(1)，f(−2)=4=f(2)，f(−3)=9=f(3)，……对于函数 ，自变量互为相反数时，对应的函数值相等．即对于定义域 R 上的任意一个x，都有f(−x)=x2=f(x)．关于函数的图像分析：对于函数f(x)=1/x有：f(−1)=−1=−f(1)，f(−2)=−1/2=−f(2)，f(−3)=−1/3=−f(3)，……事实上，对于函数，自变量互为相反数时，对应的函数值也互为相反数．即对于定义域(−∞,0)∪(0,+∞)上的任意一个x，都有 f(−x)=−1/x=−f(x)教师活动：使用精炼的语言讲解定义，讲解关键词语，学生活动：理解、记忆并尝试解决问题设计意图：通过实例让学生观察函数图像的对称情况，在教师的引导下学会用数学语言描述函数值的特征规律，引出奇偶性，培养学生逻辑推理和数学抽象等核心素养探索新知关于函数 的图像分析引出 设函数y=f(x)的定义域为数集D，若对于任意的x∈D，都有−x∈D，且f(−x)=f(x)，则称y=f(x)是偶函数．偶函数的图像关于y轴对称关于函数 的图像分析引出设函数y=f(x)的定义域为数集D，若对于任意的x∈D，都有−x∈D，且f(−x)=−f(x)，则称y=f(x)是奇函数．奇函数的图像关于原点中心对称如果一个函数是奇函数或偶函数，就说这个函数具有奇偶性，其定义域一定关于原点中心对称． 探究与发现有没有某个函数，它既是奇函数又是偶函数？如果有，请举例说明师活动：归纳总结定义，带领学生仔细分析具体情况，讲解关键词，并带领学生观察图像学生活动：观察情境思考问题，分析，回答问题并学会用语言表达自己的想法设计意图：师生共同归纳函数的奇偶性的定义，学会定性描述和定量刻画函数的奇偶性，培养学生数学抽象和逻辑推理等核心素养3、例题讲解例4 讨论下列函数的奇偶性：（1）f(x)=x3； （2）f(x)=x2+x4；（3）f(x)=x+1； （4）f(x)=．解 （1）f(x)=x3的定义域为R，对于任意的x∈R，都有−x∈R，且f(−x)=(−x)3=−x3=−f(x)，所以f(x)=x3是奇函数．（2）f(x)=x2+x4的定义域为R，对于任意的x∈R，都有−x∈R，且f(−x)=(−x)2+(−x)4=x2+x4=f(x)，所以f(x)=x2+x4是偶函数（3）f(x)=x+1的定义域为R，对于任意的x∈R，都有−x∈R，且f(−x)=−x+1≠−f(x)，f(−x)=−x+1≠f(x)，所以f(x)=x+1既不是奇函数也不是偶函数．（4）f(x)=的定义域为 ，对于1∈，而， 所以函数f(x)=既不是奇函数也不是偶函数．例5 （1）图（1）给出了偶函数y=f(x)在[ 0,+∞)上的函数图像，试将y=f(x)的图像补充完整，并指出函数的单调区间．2）图（2）给出了奇函数y=g(x)在（ 0,+∞)上的函数图像，试将y=g(x)的图像补充完整，并指出函数的单调区间．解 （1）由于函数y=f(x)是偶函数，所以它的图像关于y轴对称，因此它的图像如图所示．函数y=f(x)的减区间为(−∞,0]，增区间为[0,+∞)由于函数y=g(x)是奇函数，所以它的图像关于原点中心对称，因此它的图像如图所示．函数y=g(x)的增区间为(−∞,+∞)温馨提示 利用函数图像可以判断函数的奇偶性，根据函数的奇偶性也可以研究函数图像． 如在研究函数时，如果我们知道它是奇函数或偶函数，就可以先研究它在非负区间上的性质，然后利用对称性便可得到它在非正区间上的性质，从而减少工作量．教师活动：教师巡视指导，并对学生的回答给予指导学生活动：认真思考并答题设计意图：通过例题帮助学生理解函数的奇偶性，并学会利用定义法判断函数的奇偶性，以及利用图像的对称性完成整个函数的描画，培养学生直观形象、逻辑推理等核心素养4、巩固练习1．填空题：（1）点P(2,3)关于x轴对称的点为_____，关于y轴对称的点为 _____，关于坐标原点对称的点为_______；（2）点Q(x,y)关于x轴对称的点为_______，关于y轴对称的点为_______，关于坐标原点对称的点为_________ ．2．讨论下列函数的奇偶性：（1）f(x)=x+1/x； （2）f(x)=|x|；（3）f(x)=1−2x； （4）f(x)=x2+1．3．已知偶函数y=f(x)和奇函数y=g(x)的定义域均为[－4，4]，下图为它们在[0，4]上的图像．（1）求f(−2)与g(−2)；（2）将函数y=f(x)和y=g(x)在定义域内的图像补充完整．教师活动：提问 、巡视指导、及时指出学生的问题 学生活动：思考问题、动手做题求解答案、与小组同学交流 设计意图：通过练习及时掌握学生的知识掌握情况，查漏补缺3.3.3 几种常见的函数 1、情境引入回顾义务教育阶段学过的一次函数、反比例函数与二次函数，它们的定义域、值域、单调性、奇偶性等各是怎样的呢？如何用数学的语言表达？教师活动：引导回顾学生活动：思考分析设计意图：利用新授知识来再次认识已学函数2、探索新知1．一次函数 y=kx+b(k≠0)是一次函数，其图像为直线，如图所示． 由一次函数y=kx+b(k≠0)的解析式和图像不难发现，其定义域和值域均为 R， 并有如下性质： （1）当时，在 R 上是增函数，如图（1）所示；当时，在 R 上是减函数，如图（2）所示． （2）当b=0时，如图（3）（4）所示.一次函数y=kx(k≠0)是奇函数，其图像关于原点中心对称．教师活动：启发学生并归纳总结学生活动：思考分析并记忆设计意图：师生共同归纳一次函数的性质，对函数性质进行再认识、再提高，培养学生直观形象、逻辑推理等核心素养例题解析例6 设函数y=(3m+4)x+b在R上是减函数，求m的取值范围．解 由函数y=(3m+4)x+b在R上是减函数，可得3m+4y−1/2； 因为两个函数的图像交于点（1，4），将该点坐标代入反比例函数，得4=m2/1，所以， m=±2．由于m>−1/2，所以m=−2不合题意，舍去，故m=2一次函数为y=5x+b，将点（1，4）代入得，4=5×1+b，即b=−1．所以这个一次函数为y=5x−1，反比例函数为y=4/x．教师活动：教师巡视指导，并对学生的回答给予指导学生活动：认真思考并答题设计意图：通过例题帮助学生理解正比例函数的性质探索新知3．二次函数 y=ax2+bx+c(a≠0)是二次函数，其图像是抛物线，顶点坐标为(−b/2a,4a−b2/4a)，对称轴方程为x=−b/2a一般地，当a>0时，二次函数y=ax2+bx+c的图像是一条开口向上的抛物线，定义域为R，值域为[├ 4ac−b2/4a,+∞)．并有如下性质： （1）在(−∞,−b/2a]上是减函数，在[−b/2a,+∞) 是增函数；（2）当b=0时为偶函数．当a