物理第八章 机械能守恒定律4 机械能守恒定律教案

这是一份物理第八章 机械能守恒定律4 机械能守恒定律教案，共6页。教案主要包含了多物体机械能守恒问题的分析方法，机械能守恒定律与动能定理的异同等内容，欢迎下载使用。
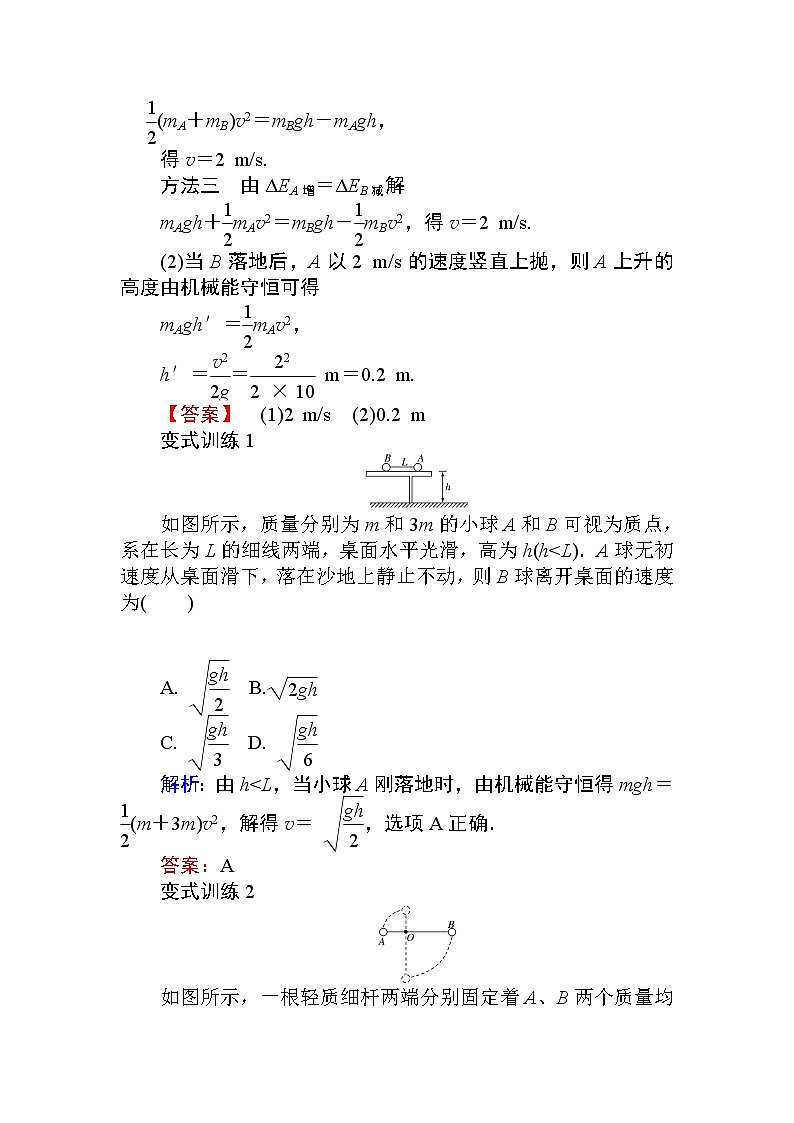
 核心素养提升微课堂科学思维系列——机械能守恒定律的综合应用一、多物体机械能守恒问题的分析方法(1)对多个物体组成的系统要注意判断物体运动过程中，系统的机械能是否守恒．(2)列机械能守恒方程时，一般选用ΔEk＝－ΔEp的形式．(3)多物体机械能守恒问题的三点注意①正确选取研究对象．②合理选取物理过程．③正确选取机械能守恒定律常用的表达形式列式求解．【例1】　如图所示，质量分别为3 kg和5 kg的物体A、B，用轻绳连接跨在一个定滑轮两侧，轻绳正好拉直，且A物体底面与地面接触，B物体距地面0.8 m，求：(1)放开B物体，当B物体着地时A物体的速度大小；(2)B物体着地后A物体还能上升多高？(g取10 m/s2)【思路点拨】　①在B下落过程中，A与B的速率时刻相等．②在B下落过程中，A、B组成的系统机械能守恒．③当B落地后，A的机械能是守恒的．【解析】　(1)方法一　由E1＝E2解对A、B组成的系统，当B下落时系统机械能守恒，以地面为零势能参考面，则mBgh＝mAgh＋(mA＋mB)v2v＝ ＝  m/s＝2 m/s.方法二　由ΔEk增＝ΔEp减解(mA＋mB)v2＝mBgh－mAgh，得v＝2 m/s.方法三　由ΔEA增＝ΔEB减解mAgh＋mAv2＝mBgh－mBv2，得v＝2 m/s.(2)当B落地后，A以2 m/s的速度竖直上抛，则A上升的高度由机械能守恒可得mAgh′＝mAv2，h′＝＝ m＝0.2 m.【答案】　(1)2 m/s　(2)0.2 m变式训练1　如图所示，质量分别为m和3m的小球A和B可视为质点，系在长为L的细线两端，桌面水平光滑，高为h(h<L)．A球无初速度从桌面滑下，落在沙地上静止不动，则B球离开桌面的速度为(　　)  A.   B.C.   D. 解析：由h<L，当小球A刚落地时，由机械能守恒得mgh＝(m＋3m)v2，解得v＝ ，选项A正确．答案：A变式训练2　如图所示，一根轻质细杆两端分别固定着A、B两个质量均为m的小球，O点是光滑水平轴的转动点．已知AO＝L，BO＝2L.使细杆从水平位置由静止开始转动，当B球转到O点正下方时，它对细杆的拉力是多大？解析：设B球到达O点的正下方时，A、B两球的速度分别为vA、vB.两球在转动过程中角速度相等，由v＝ωr得vAvB＝L2L＝12①对A、B组成的系统应用机械能守恒定律ΔEp减＝ΔEk增，有mg×2L－mgL＝mv＋mv②由①②式联立解得vB＝③B球在O点正下方时，由向心力公式，有F－mg＝m④将③式代入④式得F＝mg＋m＝1.8mg.由牛顿第三定律可得，B球对细杆的拉力大小F′＝F＝1.8mg.答案：1.8 mg二、机械能守恒定律与动能定理的异同  机械能守恒定律动能定理不同点适用条件只有重力或弹力做功没有条件限制，它不但允许重力和弹力做功，还允许其他力做功分析思路只需分析研究对象初、末状态的动能和势能即可不但要分析研究对象初、末状态的动能，还要分析所有外力所做的功研究对象一般是物体组成的系统一般是一个物体(质点)书写方式有多种书写方式，一般常用等号两边都是动能与势能的和等号左边一定是合力的总功，右边则是动能的变化相同点(1)思想方法相同：机械能守恒定律和动能定理都是从做功和能量转化的角度，来研究物体在力的作用下状态的变化(2)表达这两个规律的方程都是标量式【例2】　如图所示，AB是竖直面内的四分之一圆弧光滑轨道，下端B与水平直轨道相切．一个小物块自A点由静止开始沿轨道下滑，已知轨道半径为R＝0.2 m，小物块的质量为m＝0.1 kg，小物块与水平面间的动摩擦因数μ＝0.5，取g＝10 m/s2.求：(1)小物块到达B点的速度大小；(2)小物块在B点时受圆弧轨道的支持力；(3)小物块在水平面上滑动的最大距离．【解析】　(1)对小物块从A下滑到B，根据机械能守恒定律，得：mgR＝mv，解得：vB＝＝2.0 m/s.(2)对小物块在B点，由牛顿第二定律得：FN－mg＝m将vB＝代入，可得：FN＝3mg＝3×0.1×10 N＝3 N.(3)设在水平面上滑动的最大距离为s.对小物块在水平面上的滑动过程，由动能定理得：－μmgs＝0－mv解得：s＝＝ m＝0.4 m.【答案】　(1)2.0 m/s　(2)3 N　(3)0.4 m变式训练3　如图所示，小球从高h的光滑斜面上滚下，经有摩擦的水平地面再滚上另一光滑斜面，当它到达h高度时，速度变为0，求小球最终停在何处．解析：设小球在A、B两点的速度为vA、vB，则有mgh＝mv①mgh＝mv②在水平地面上，摩擦力Ff做的功等于小球动能的变化－Ff·xAB＝mv－mv③联立①②③式解得xAB＝④小球最后停下，由动能定理得－Ff·x′＝0－mv⑤联立②⑤式得x′＝⑥联立④⑥式得x′＝xAB故小球最终停在AB的中点处．答案：小球停在AB中点变式训练4　为了研究过山车的原理，某兴趣小组提出了下列设想：取一个与水平方向夹角为37°、长为L＝2.0 m的粗糙倾斜轨道AB，通过水平轨道BC与半径为R＝0.2 m的竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的．其中AB与BC轨道以微小圆弧相接，如图所示．一个质量m＝1 kg的小物块以初速度v0＝5.0 m/s从A点沿倾斜轨道滑下，小物块到达C点时速度vC＝4.0 m/s.取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8.(1)求小物块到达C点时对圆轨道压力的大小；(2)求小物块从A到B运动过程中摩擦力所做的功；(3)为了使小物块不离开轨道，并从轨道DE滑出，求竖直圆轨道的半径应满足什么条件？解析：(1)设小物块到达C点时受到圆轨道的支持力大小为FN，根据牛顿第二定律有，FN－mg＝m，解得FN＝90 N．根据牛顿第三定律，小物块对圆轨道压力的大小为90 N.(2)由于水平轨道BC光滑，无摩擦力做功，所以可将研究小物块从A到B的运动过程转化为研究从A到C的过程．物块从A到C的过程中，根据动能定理有：mgLsin 37°＋Wf＝mv－mv解得Wf＝－16.5 J.(3)设小物块进入圆轨道到达最高点时速度大小为v，根据牛顿第二定律有：FN＋mg＝m，且FN≥0小物块从圆轨道最低点到最高点的过程中，根据机械能守恒定律有：mv＝mv2＋mg·2R，联立得R≤，解得R≤0.32 m.答案：(1)90 N　(2)－16.5 J　(3)R≤0.32 m