

高中数学必修一 第五章 三角函数 章末复习教学设计
展开
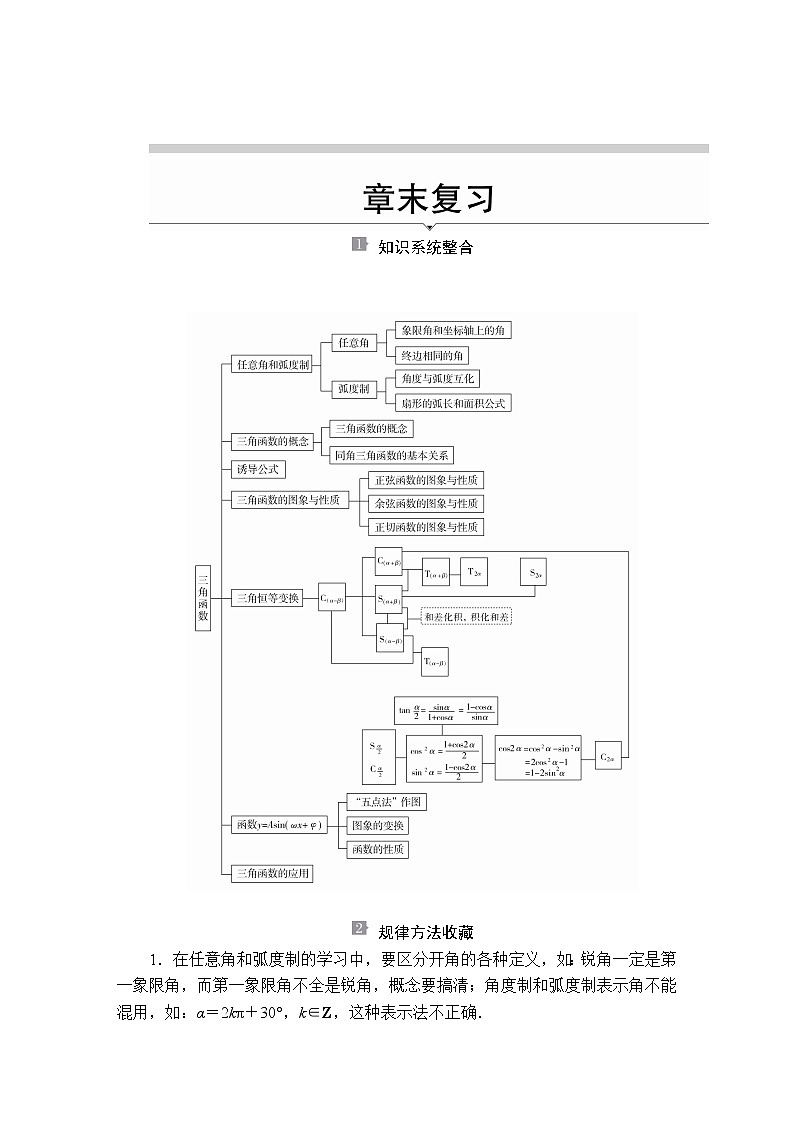
知识系统整合
规律方法收藏
1.在任意角和弧度制的学习中,要区分开角的各种定义,如:锐角一定是第一象限角,而第一象限角不全是锐角,概念要搞清;角度制和弧度制表示角不能混用,如:α=2kπ+30°,k∈Z,这种表示法不正确.
2.任意角的三角函数,首先要考虑定义域,其次要深刻认识三角函数符号的含义,sinα=≠sin×α;诱导公式的记忆要结合三角函数的定义去记忆.
3.同角三角函数的基本关系式
sin2α+cos2α=1及=tanα,必须牢记这两个基本关系式,并能应用它们进行三角函数的求值、化简、证明,在应用中,注意掌握解题的技巧,能灵活运用公式.在应用平方关系求某个角的另一个三角函数值时,要注意根式前面的符号的确定.
4.三角函数的诱导公式
诱导公式一至六不仅要正确、熟练地掌握其记忆的诀窍,更要能灵活地运用.
(1)-α角的三角函数是把负角转化为正角;
(2)2kπ+α(k∈Z)角的三角函数是化任意角为[0,2π)内的角;
(3)±α,π±α,±α,2π-α角的三角函数是化非锐角为锐角;
(4)化负为正→化大为小→化为锐角;
(5)记忆规律:奇变偶同,象限定号.
5.正弦函数、余弦函数的图象与性质
(1)五点法作图是画三角函数图象的基本方法,要切实掌握,作图时自变量要用弧度制,作出的图象要正规.
(2)奇偶性、单调性、最值、周期是三角函数的重要性质,f(x+T)=f(x)应强调的是自变量x本身加常数才是周期,如f(2x+T)=f(2x),T不是f(2x)的周期.
解答三角函数的单调性的题目一定要注意复合函数单调性法则,更要注意定义域.
6.使用本章公式时,应注意公式的正用、逆用以及变形应用.如两角和与差的正切公式tan(α±β)=,其变形公式:tanα±tanβ=tan(α±β)(1∓tanαtanβ)应用广泛;公式cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α的变形公式:1+cos2α=2cos2α,1-cos2α=2sin2α,cos2α=,sin2α=常用来升幂或降幂.
7.函数y=Asin(ωx+φ)
主要掌握由函数y=sinx的图象到函数y=Asin(ωx+φ)的图象的平移、伸缩等变换.
注意各种变换对图象的影响,注意各物理量的意义,A,ω,φ与各种变换的关系.
8.三角函数的应用
(1)根据图象建立解析式;
(2)根据解析式作出图象;
(3)将实际问题抽象为与三角函数有关的函数模型;
(4)利用收集到的数据作出散点图,并根据散点图进行函数模拟.
在建立三角函数模型的时候,要注意从数据的周而复始的特点以及数据变化趋势两个方面来考虑.
学科思想培优
一、三角函数变形的常见方法
在进行三角函数式的化简或求值时,细心观察题目的特征,灵活、恰当地选用公式,统一角、统一函数、降低次数是三角函数关系式变形的出发点.
在本章所涉及的变形中,常用的变形方法有切化弦、弦化切和“1”的代换.
1.切化弦
当三角函数式中三角函数名称较多时,往往把三角函数化为弦,再化简变形.
[典例1] 求证:sinθ(1+tanθ)+cosθ=+.
证明 左边=sinθ+cosθ
=sinθ++cosθ+
=+
=+
=+=右边.
[典例2] 求证:·=1.
证明 ·=·
=·===1.
2.弦化切
已知tanα的值,求关于sinα,cosα的齐次分式(sinα,cosα的次数相同)的值,可将求值式变为关于tanα的代数式,此方法亦称为“弦化切”.
[典例3] 已知tanα=-,求下列各式的值:
(1);
(2)2sin2α+sinαcosα-3cos2α.
解 (1)∵tanα=-,
∴===-.
(2)2sin2α+sinαcosα-3cos2α
==
==-.
[典例4] 已知2cos2α+3cosαsinα-3sin2α=1,α∈.求:
(1)tanα;
(2).
解 (1)2cos2α+3cosαsinα-3sin2α
==,
则=1,
即4tan2α-3tanα-1=0.
解得tanα=-或tanα=1.
∵α∈,∴α为第二象限角,
∴tanα<0,∴tanα=-.
(2)原式====.
3.“1”的代换
在三角函数中,有时会含有常数1,常数1虽然非常简单,但有些三角函数式的化简却需要利用三角函数公式将1代换为三角函数式,常见的代换方法:1=sin2α+cos2α等.
[典例5] 求证:=.
证明 左边=
=
===右边.
∴等式成立.
[典例6] 已知tan2α=2tan2β+1,求证:sin2β=2sin2α-1.
证明 ∵tan2α=2tan2β+1,
∴tan2α+1=2(tan2β+1).
∴=2·.
∴=.
∴cos2β=2cos2α.
∴1-sin2β=2(1-sin2α).
∴sin2β=2sin2α-1.
二、求三角函数值域与最值的常见类型
求三角函数的值域或最值主要依据是利用三角函数的图象或三角函数的有界性,这就要求我们必须掌握好三角函数的图象和性质.
1.形如y=asinx+b(a≠0)型的函数
求解形如y=asinx+b(或y=acosx+b)的函数的最值或值域问题时,利用正、余弦函数的有界性(-1≤sinx,cosx≤1)求解,注意对a正、负的讨论.
[典例7] 若y=asinx+b的最大值为3,最小值为1,求ab的值.
解 当a>0时,解得
当a<0时,解得
∴ab=2或ab=-2.
[典例8] 求函数y=3-4cos,x∈的最大、最小值及相应的x值.
解 ∵x∈,∴2x+∈,
从而-≤cos≤1.
∴当cos=1即2x+=0,
即x=-时,ymin=3-4=-1,
当cos=-即2x+=,
即x=时,ymax=3-4×=5.
2.形如y=asin2x+bsinx+c(a≠0)型的函数
求解形如y=asin2x+bsinx+c(或y=acos2x+bcosx+c),x∈D的函数的值域或最值时,通过换元,令t=sinx(或cosx),将原函数转化为关于t的二次函数,利用配方法求值域或最值即可.求解过程中要注意t=sinx(或cosx)的有界性.
[典例9] 求函数f(x)=2sin2x+2sinx-,x∈的值域.
解 令t=sinx,y=f(x),
∵x∈,∴≤sinx≤1,即≤t≤1.
∴y=2t2+2t-=22-1,
∴1≤y≤,
∴函数f(x)的值域为.
[典例10] 已知|x|≤,求函数y=-sin2x+sinx+1的最小值.
解 令t=sinx,因为|x|≤,
所以-≤sinx≤,即t∈,
则y=-t2+t+1=-2+,t∈.
根据二次函数的性质可得当t=-,即x=-时,y有最小值,为-2+=.
三、三角函数的化简
在具体实施过程中,应着重抓住“角”的统一.通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升幂、降幂、逆用公式等手段将其化简.最后结果应为:(1)能求值尽量求值;(2)三角函数名称尽量少;(3)项数尽量少;(4)次数尽量低;(5)分母、根号下尽量不含三角函数.
[典例11] 化简:.
解 原式=
=
=
=
=
=
==2.
四、三角函数求值
三角函数求值主要有三种类型,即:
(1)“给角求值”,一般给出的角都是非特殊角,从表面看较难,但仔细观察就会发现这类问题中的角与特殊角都有一定的关系,如和或差为特殊角,当然还有可能需要运用诱导公式.
(2)“给值求值”,即给出某些角的三角函数式的值,求另外一些三角函数的值,这类求值问题关键在于结合条件和结论中的角,合理拆、配角.当然在这个过程中要注意角的范围.
(3)“给值求角”,本质上还是“给值求值”,只不过往往求出的是特殊角的值,在求出角之前还需结合函数的单调性确定角,必要时还要讨论角的范围.
[典例12] 已知cos=-,sin=,且α∈,β∈,求:
(1)cos;
(2)tan(α+β).
解 (1)∵<α<π,0<β<,
∴<α-<π,-<-β<,
∴sin==,
cos==,
∴cos=cos
=coscos+sinsin
=-×+×=-.
(2)∵<<,
∴sin==.
∴tan==-.
∴tan(α+β)==.
[典例13] 已知tanα=4,cos(α+β)=-,α,β均为锐角,求cosβ的值.
解 因为α,β均为锐角,所以0<α+β<π,
又cos(α+β)=-,所以<α+β<π,
且sin(α+β)=.
因为tanα=4,所以sinα=,cosα=.
所以cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα=.
五、三角恒等证明
三角恒等式的证明,就是应用三角公式,通过适当的恒等变换,消除三角恒等式两端结构上的差异,这些差异有以下几方面:①角的差异;②三角函数名称的差异;③三角函数式结构形式上的差异.针对上面的差异,选择合适的方法进行等价转化.
[典例14] 求证:tan2x+=.
证明 证法一:左边=+=
==
===
===右边.
原式得证.
证法二:右边==
=
=
==tan2x+=左边.
原式得证.
六、三角函数的图象
三角函数的图象是研究三角函数性质的基础,又是三角函数性质的具体体现.在平时的考查中,主要体现在三角函数图象的变换和解析式的确定,以及通过对图象的描绘、观察来讨论函数的有关性质.
[典例15] 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.
(1)求此函数的解析式;
(2)分析一下该函数的图象是如何通过y=sinx的图象变换得来的?
解 (1)由图象知
A==,
k==-1,
T=2×=π,
∴ω==2.
∴y=sin(2x+φ)-1.
当x=时,2×+φ=,
∴φ=.
∴所求函数的解析式为y=sin-1.
(2)把y=sinx的图象向左平移个单位长度,得到y=sin的图象,然后纵坐标保持不变、横坐标缩短为原来的,得到y=sin的图象,再横坐标保持不变,纵坐标变为原来的,得到y=sin的图象,最后把函数y=sin的图象向下平移1个单位长度,得到y=sin-1的图象.
七、三角函数的性质
1.三角函数的性质,重点应掌握函数y=sinx,y=cosx,y=tanx的定义域、值域、单调性、奇偶性、周期性,在此基础上,掌握函数y=Asin(ωx+φ),y=Acos(ωx+φ)及y=Atan(ωx+φ)的相关性质.
2.该热点是三角函数的重中之重,考查的形式也不唯一,主、客观题均有体现,在难度上较前两热点有所增加,主观题以中档题为主,知识间的联系相对加大.
[典例16] 已知函数f(x)=logacos(其中a>0,且a≠1).
(1)求它的定义域;
(2)求它的单调区间;
(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的周期.
解 (1)由题意知cos>0,
∴2kπ-<2x-<2kπ+(k∈Z),
即kπ-<x<kπ+(k∈Z).
故函数的定义域为(k∈Z).
(2)在定义域范围内求cos的单调区间.
函数u=cos在(k∈Z)上单调递增,在(k∈Z)上单调递减,
∴当a>1时,
f(x)的单调增区间为(k∈Z),
单调减区间为(k∈Z);
当0<a<1时,
f(x)的单调增区间为(k∈Z),
单调减区间为(k∈Z).
(3)∵函数f(x)的定义域不关于原点对称,
∴函数f(x)既不是奇函数,也不是偶函数.
(4)函数f(x)是周期函数,
∵f(x+π)=logacos
=logacos=f(x),
∴函数f(x)的周期为T=π.









