内蒙古通辽市奈曼旗六校2022届九年级下学期期中综合素质测评数学试卷(含答案)

2021---2022学年第二学期期中综合素质测评

数学学科（九年级）

一、选择题（本题共10小题，每小题3分，共30分）

1.在实数|﹣3.14|，﹣3，﹣，﹣π 中，最小的数是（　　）

A．﹣ B．﹣3 C．|﹣3.14| D．﹣π

2.如图所示的工件的主视图是（　　）

A． B． C． D．

3.下列调查中，适宜采用普查方式的是（　　）

A．调查市场上冷冻食品的质量情况 

B．调查乘坐飞机的旅客是否携带了危禁物品 

C．调查某品牌冰箱的使用寿命 

D．调查2021年春晚的收视率情况

4.将抛物线C1：y＝（x﹣3）2+2向左平移3个单位长度，得到抛物线C2，抛物线C2与抛物线C3关于x轴对称，则抛物线C3的解析式为（　　）

A．y＝x2﹣2 B．y＝﹣x2+2 C．y＝x2+2 D．y＝﹣x2﹣2

5.定义运算：m☆n＝mn2﹣mn+1．例如：3☆2＝3×22﹣3×2+1＝7，则方程4☆x＝0的根的情况为（　　）

A．有两个不相等的实数根 B．有两个相等的实数根 

C．无实数根 D．只有一个实数根

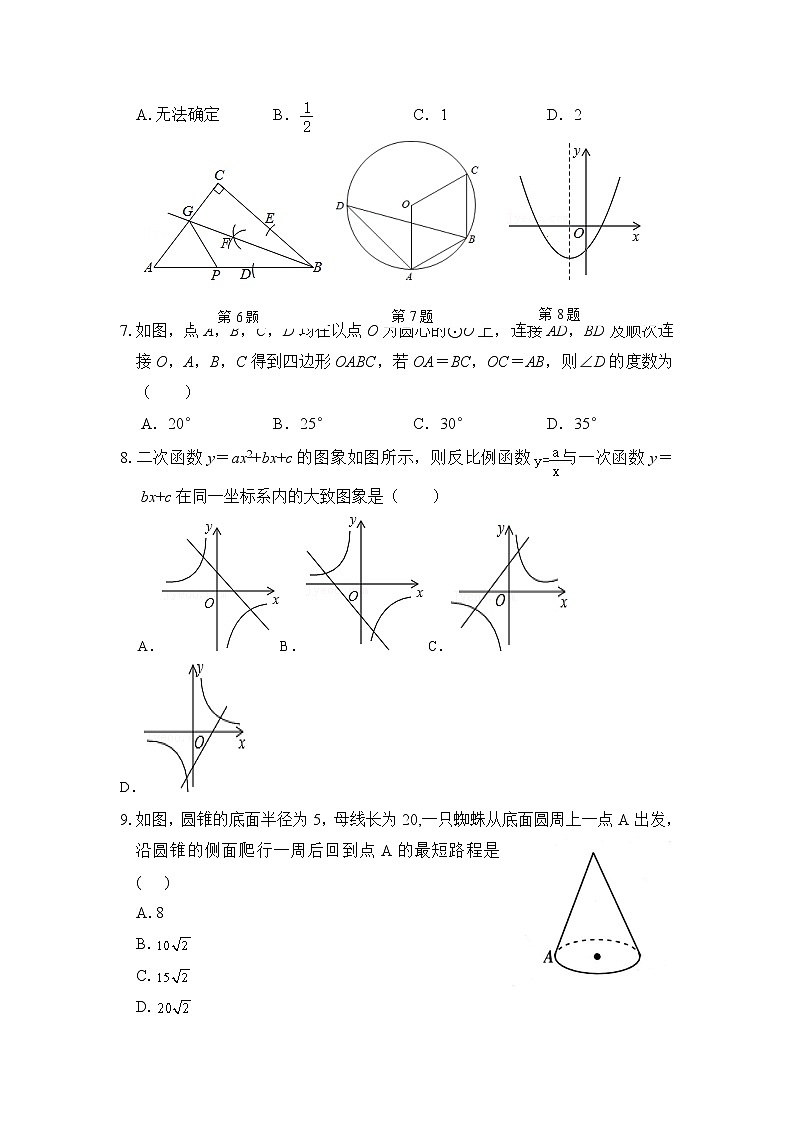
6.如图，Rt△ABC中，∠C＝90°，利用尺规在BC，BA上分别截取BE，BD，使BE＝BD；分别以D，E为圆心、以大于DE的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G．若CG＝1，P为AB上一动点，则GP的最小值为（　　）

A.无法确定 B． C．1 D．2

7.如图，点A，B，C，D均在以点O为圆心的⊙O上，连接AD，BD及顺次连接O，A，B，C得到四边形OABC，若OA＝BC，OC＝AB，则∠D的度数为（　　）

A．20° B．25° C．30° D．35°

8.二次函数y＝ax2+bx+c的图象如图所示，则反比例函数与一次函数y＝bx+c在同一坐标系内的大致图象是（　　）                           

A．B． C．D．

9.如图，圆锥的底面半径为5，母线长为20,一只蜘蛛从底面圆周上一点A出发，沿圆锥的侧面爬行一周后回到点A的最短路程是(   )

  A.8  

B.  

C.  

D.

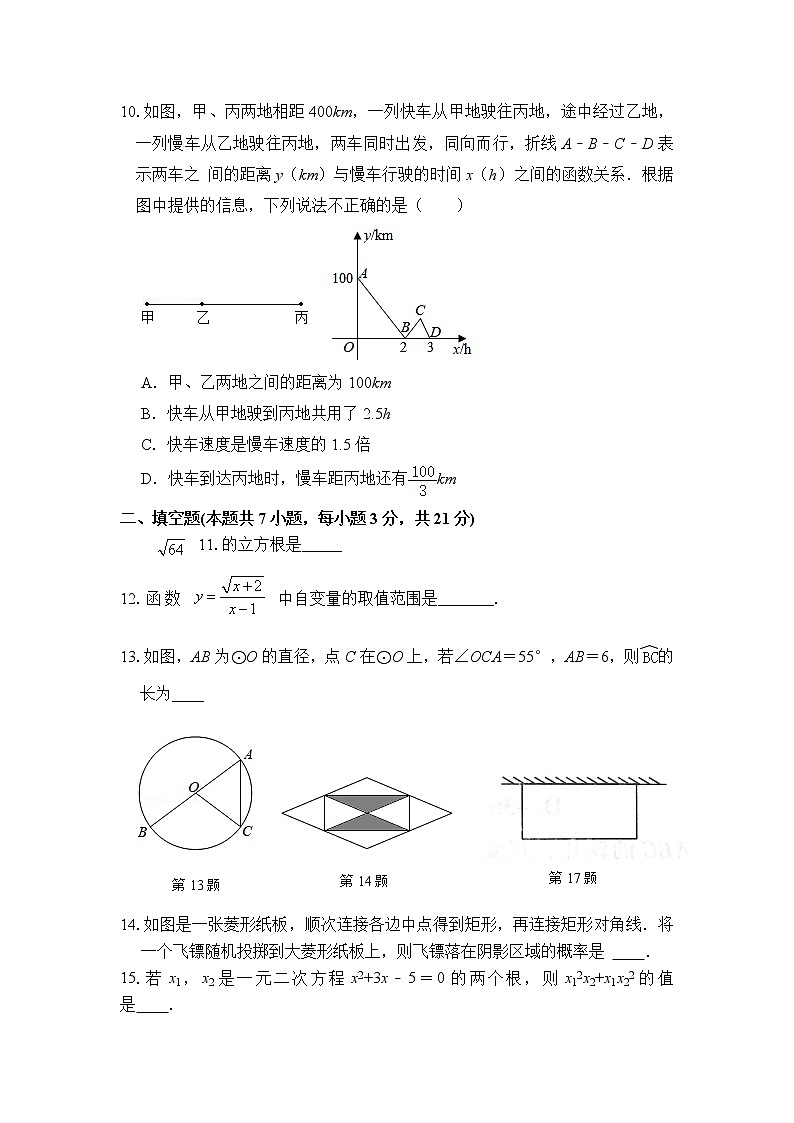
10.如图，甲、丙两地相距400km，一列快车从甲地驶往丙地，途中经过乙地，一列慢车从乙地驶往丙地，两车同时出发，同向而行，折线A﹣B﹣C﹣D表示两车之 间的距离y（km）与慢车行驶的时间x（h）之间的函数关系．根据图中提供的信息，下列说法不正确的是（　　）

A．甲、乙两地之间的距离为100km 

B．快车从甲地驶到丙地共用了2.5h 

C．快车速度是慢车速度的1.5倍 

D．快车到达丙地时，慢车距丙地还有km

二、填空题(本题共7小题，每小题3分，共21分)

11.的立方根是_____

12.函数         中自变量的取值范围是_______.

13.如图，AB为⊙O的直径，点C在⊙O上，若∠OCA＝55°，AB＝6，则的

长为____

14.如图是一张菱形纸板，顺次连接各边中点得到矩形，再连接矩形对角线．将一个飞镖随机投掷到大菱形纸板上，则飞镖落在阴影区域的概率是 　　．

15.若x1，x2是一元二次方程x2+3x﹣5＝0的两个根，则x12x2+x1x22的值是　　．

16.若关于的方程的解是正数，则的取值范围为_________．

17.如图，用10 m长的篱笆围成一个一面靠墙的矩形场地，墙的最大长度为4 m。

则场地的最大面积为_____m2.

三、解答题（本题包括9小题，共计69分）

18.(4分)计算：

19.(6分)先化简，再求值：，其中x2+3x﹣5＝0．

20.(6分)学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表．

学生借阅图书的次数统计表

请你根据统计图表中的信息，解答下列问题：

（1）a＝　   　，b＝　   　．

（2）该调查统计数据的中位数是　   　，众数是　   　．

（3）请计算扇形统计图中“3次”所对应扇形的圆心角的度数；

（4）若该校共有2000名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的人数．

21.（6分）随着“新冠肺炎”疫情防控形势日渐好转，各地开始复工复学，某校复学后成立“防疫志愿者服务队”，设立四个“服务监督岗”：①洗手监督岗，②戴口罩监督岗，③就餐监督岗，④操场活动监督岗．李老师和王老师报名参加了志愿者服务工作，学校将报名的志愿者随机分配到四个监督岗．

（1）李老师被分配到“洗手监督岗”的概率为______ ；

（2）用列表法或画树状图法，求李老师和王老师被分配到同一个监督岗的概

率.

22．(7分)某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动，他们制订了测量方案，并利用课余时间实地测量．

请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔AB的高度．

（精确到0.1米，参考数据：sin32°≈0.52，cos32°≈0.84，tan32°≈0.62）

23.(8分)如图，等腰△ABC中，AB＝AC，AD⊥BC交BC于D点，E点是AB的中点，分别过D，E两点作线段AC的垂线，垂足分别为G，F两点．

（1）求证：四边形DEFG为矩形；

（2）若AB＝10，EF＝4，求CG的长．

24.(10分)2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢．某商家两次购进冰墩墩进行销售，第一次用22000元，很快销售一空，第二次又用48000元购进同款冰墩墩，所购进数量是第一次的2倍，但单价贵了10元．

（1）求该商家第一次购进冰墩墩多少个？

（2）若所有冰墩墩都按相同的标价销售，要求全部销售完后的利润率不低于20%（不考虑其他因素），那么每个冰墩墩的标价至少为多少元？

25.(10分)如图，BD为⊙O的直径，AB为⊙O的切线，过点A的直线与⊙O分别交于点E，C，与BD交于点F，连接BE，BC．

（1）求证：∠ABE＝∠BCA．

（2）若∠A＝∠ABE，BE＝EF，BE＝5，BC＝8，求⊙O的半径．

26.(12分)如图，已知抛物线y＝﹣x2+bx+c交x轴于A（﹣3，0），B（4，0）两点，交y轴于点C，点P是抛物线上一点，连接AC、BC．

（1）求抛物线的表达式；

（2）连接OP，BP，若S△BOP＝2S△AOC，求点P的坐标；

（3）在抛物线的对称轴上是否存在点Q，使得∠QBA＝75°？若存在，直接写出点Q的坐标；若不存在，请说明理由．