_四川省达州市达川四中联盟2022-2023学年七年级上学期期中数学试卷 (含答案)

这是一份_四川省达州市达川四中联盟2022-2023学年七年级上学期期中数学试卷 (含答案)，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．下列各式中，负数是（ ）
A．|﹣5|B．（﹣1）2021C．﹣（﹣3）D．（﹣5）2
2．2021年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”．在制动捕获过程中，探测器距离地球的距离为192000000公里．数字192000000用科学记数法表示为（ ）
A．19.2×107B．19.2×108C．1.92×108D．1.92×109
3．下列立体图形中，其左视图与另外三个立体图形的左视图不可能相同的是（ ）
A．B．C．D．
4．A点为数轴上表示﹣2的点，则距A点4个单位长度的点所表示的数为（ ）
A．2B．﹣6C．2或﹣6D．﹣4或4
5．已知图1的小正方形和图2中所有的小正方形都全等，将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置，放置后所组成的图形是不能围成一个正方体的．那么安放的位置是（ ）
A．①B．②C．③D．④
6．在数轴上，一只蚂蚁从原点出发，它第一次向右爬行了一个单位长度，第二次接着向左爬行了2个单位长度，第三次接着向右爬行了3个单位长度，第四次接着向左爬行了4个单位长度，如此进行了2020次，问蚂蚁最后在数轴上什么位置？（ ）
A．﹣1010B．﹣1009C．1009D．1010
7．有三个正方体木块，每一块的各面都写上不同的数字，三块的写法完全相同，现把它们摆放成如图所示的位置请你判断数字5对面的数字是（ ）
A．1B．2C．3D．6
8．a，b，c大小关系如图，下列各式①a﹣b﹣c＜0；②++＝1；③ac﹣b＞0；④|a﹣c|﹣|a+b|＝c+b，其中错误的个数为（ ）
A．1个B．2个C．3个D．4个
二、填空题（每小题4分，共20分）
9．某粮店出售的三种品牌的面粉袋上，分别标有质量为（25±0.1）kg，（25±0.2）kg，（25±0.3）kg的字样，从中任意拿出两袋，它们的质量最多相差 ．
10．小江同学与小北同学约定了一种新运算：a△b＝3a﹣2b．小江同学尝试计算2△5＝3×2﹣2×5＝6﹣10＝﹣4，现在请小北同学计算2△（﹣5）＝ ．
11．计算：20×（﹣5）＝ ．
12．若代数式3x+2与代数式5x﹣10的值互为相反数，则x＝
13．如图①是一个小正方体的侧面展开图，小正方体从如图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格，这时小正方体朝上面的字是 ．
三、解答题（共计48分）
14．把下列各数分别填在相应的集合内：
﹣11，4.8，73，﹣2.7，，3.14，﹣，，0．
正分数集合：{ …}；
负有理数集合：{ …}；
整数集合：{ …}；
非正整数集合：{ …}．
15．计算：
（1）（﹣4）﹣（﹣2）+（﹣9）+3.5；
（2）1÷（0.75）×（﹣1）÷3×（﹣0.5）2；
（3）（﹣3）2﹣（1）3×﹣6÷；
（4）（﹣3+﹣）×（﹣36）．
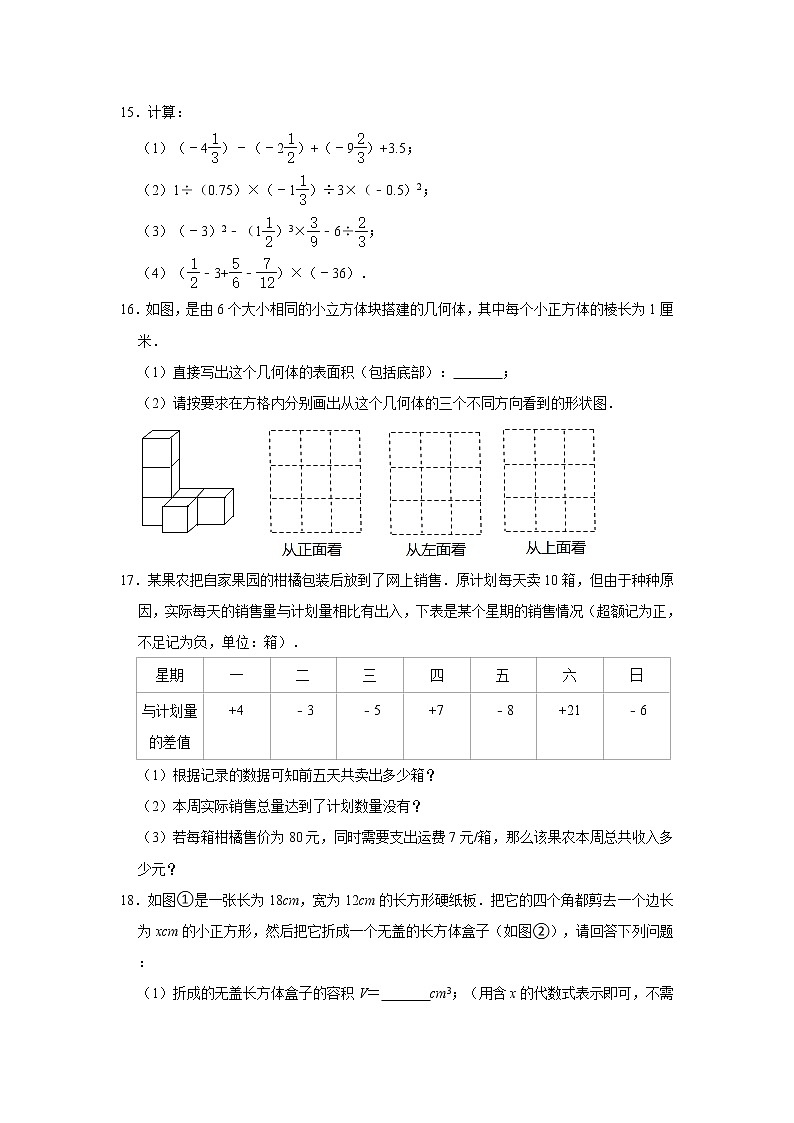
16．如图，是由6个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．
（1）直接写出这个几何体的表面积（包括底部）： ；
（2）请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．
17．某果农把自家果园的柑橘包装后放到了网上销售．原计划每天卖10箱，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某个星期的销售情况（超额记为正，不足记为负，单位：箱）．
（1）根据记录的数据可知前五天共卖出多少箱？
（2）本周实际销售总量达到了计划数量没有？
（3）若每箱柑橘售价为80元，同时需要支出运费7元/箱，那么该果农本周总共收入多少元？
18．如图①是一张长为18cm，宽为12cm的长方形硬纸板．把它的四个角都剪去一个边长为xcm的小正方形，然后把它折成一个无盖的长方体盒子（如图②），请回答下列问题：
（1）折成的无盖长方体盒子的容积V＝ cm3；（用含x的代数式表示即可，不需化简）
（2）请完成下表，并根据表格回答，当x取什么正整数时，长方体盒子的容积最大？
（3）从正面看折成的长方体盒子，它的形状可能是正方形吗？如果是正方形，求出x的值；如果不是正方形，请说明理由．
一、填空题（每小题4分，共计20分）
19．计算：÷（）＝ ．
20．已知|a|＝4且a＜0，b是绝对值最小的数，c是最大的负整数，则a+b﹣c＝ ．
21．如图为一个用正方体积木搭成的几何体的三视图，俯视图中方格上的数字表示该位置上积木累积的个数．若保证正视图和左视图成立，则a+b+c+d的最大值为 ．
22．如图，一个正方体截去一个角后，剩下的几何体有 个面，有 条棱．
23．阅读下列材料，并解决后面的问题．
材料：一般地，n个相同的因数a相乘：记为．如23＝8，此时，3叫做以2为底8的对数，记为lg28（即lg28＝3）．一般地，若an＝b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为lgab（即lgab＝n）．如34＝81，则4叫做以3为底81的对数，记为lg381（即lg381＝4）．则lg24，lg216，lg264之间满足的关系式为 ．
二、解答题
24．若a，b互为相反数，c，d互为倒数，且|x﹣2|＝5．求：x﹣（a+b+cd）+|（a+b）﹣4|﹣（﹣cd）2021的值．
25．观察下列等式＝1﹣，＝﹣，＝﹣，将以上三个等式两边分别相加得++＝1﹣+﹣+﹣＝1﹣＝．
（1）猜想并写出＝ ；
（2）+++…+＝ ；
（3）探究并计算：+++…+；
（4）计算：++++++++．
26．已知数轴上点A，O，P所表示的数分别是﹣3，0，x点P在线段AO上．
（1）请在数轴上标出A，O两点；
（2）①线段AP＝ （用含x的式子表示）
②在点P右侧的数轴上画线段PQ＝AP，当OP＝2OQ时，求x的值．
参考答案
一、选择题（每小题4分，共计32分）
1．下列各式中，负数是（ ）
A．|﹣5|B．（﹣1）2021C．﹣（﹣3）D．（﹣5）2
【分析】直接利用绝对值的性质以及有理数的乘方运算法则分别化简得出答案．
解：A、|﹣5|＝5，不合题意；
B、（﹣1）2021＝﹣1，符合题意；
C、﹣（﹣3）＝3，不合题意；
D、（﹣5）2＝25，不合题意；
故选：B．
【点评】此题主要考查了绝对值的性质以及有理数的乘方运算等知识，正确掌握相关定义是解题关键．
2．2021年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”．在制动捕获过程中，探测器距离地球的距离为192000000公里．数字192000000用科学记数法表示为（ ）
A．19.2×107B．19.2×108C．1.92×108D．1.92×109
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．据此解答即可．
解：192000000＝1.92×108，
故选：C．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要确定a的值以及n的值．
3．下列立体图形中，其左视图与另外三个立体图形的左视图不可能相同的是（ ）
A．B．C．D．
【分析】从左面看到的图形是左视图，进而分别判断得出答案．
解：因为圆柱的左视图是长方形，圆锥的左视图是三角形，长方体的左视图是长方形，三棱柱的左视图是长方形，
所以圆锥的左视图与另外三个立体图形的左视图不可能相同．
故选：B．
【点评】此题主要考查了三视图，解题的关键是把握好三视图所看的方向．属于基础题，中考常考题型．
4．A点为数轴上表示﹣2的点，则距A点4个单位长度的点所表示的数为（ ）
A．2B．﹣6C．2或﹣6D．﹣4或4
【分析】根据题意，可以写出距A点4个单位长度的点所表示的数，本题得以解决．
解：∵点A为数轴上表示﹣2的点，
∴距A点4个单位长度的点所表示的数为﹣2+4＝2或﹣2﹣4＝﹣6，
即距A点4个单位长度的点所表示的数为2或﹣6，
故选：C．
【点评】本题考查数轴，解答本题的关键是明确题意，利用数轴的知识解答．
5．已知图1的小正方形和图2中所有的小正方形都全等，将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置，放置后所组成的图形是不能围成一个正方体的．那么安放的位置是（ ）
A．①B．②C．③D．④
【分析】由平面图形的折叠及正方体的表面展开图的特点解题．
解：将图1的正方形放在图2中的①的位置出现重叠的面，所以不能围成正方体．
故选：A．
【点评】本题考查了展开图折叠成几何体，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．注意：只要有“田”字格的展开图都不是正方体的表面展开图．
6．在数轴上，一只蚂蚁从原点出发，它第一次向右爬行了一个单位长度，第二次接着向左爬行了2个单位长度，第三次接着向右爬行了3个单位长度，第四次接着向左爬行了4个单位长度，如此进行了2020次，问蚂蚁最后在数轴上什么位置？（ ）
A．﹣1010B．﹣1009C．1009D．1010
【分析】一只蚂蚁从原点出发，它第一次向右爬行了一个单位长度到达1，第二次接着向左爬行了2个单位长度到达﹣1，第三次接着向右爬行了3个单位长度到达2，第四次接着向左爬行了4个单位长度到达﹣2，依此类推得到一般性规律，即可得到结果．
解：一只蚂蚁从原点出发，它第一次向右爬行了一个单位长度到达1，第二次接着向左爬行了2个单位长度到达﹣1，第三次接着向右爬行了3个单位长度到达2，第四次接着向左爬行了4个单位长度到达﹣2，依此类推，第2020次到达﹣1010
则蚂蚁最后在数轴上﹣1010位置，
故选：A．
【点评】此题考查了数轴，弄清题中的规律是解本题的关键．
7．有三个正方体木块，每一块的各面都写上不同的数字，三块的写法完全相同，现把它们摆放成如图所示的位置请你判断数字5对面的数字是（ ）
A．1B．2C．3D．6
【分析】根据正方体的表面展开图的特征进行判断即可．
解：根据第一个和第二个正方体表面的数字可知，“4”的邻面是“1、6、2、5”，因此“4”的对面是“3”，
由第二个和第三个正方体表面的数字可知，“2”的邻面是“4、5、3、6”，因此“2”的对面是“1”，
所以“5”和“6”是对面，
故选：D．
【点评】本题考查正方体的展开与折叠，掌握正方体表面展开图的特征是正确判断的前提．
8．a，b，c大小关系如图，下列各式①a﹣b﹣c＜0；②++＝1；③ac﹣b＞0；④|a﹣c|﹣|a+b|＝c+b，其中错误的个数为（ ）
A．1个B．2个C．3个D．4个
【分析】利用a，b，c在数轴上的位置确定a，b，c的符号，进而确定﹣b，﹣c，ac，a﹣c，a+b的符号，利用有理数运算确定符号的法则以及绝对值的意义对每个结论进行判断即可得出结论．
解：由题意得：
a＜0，b＞0，c＞0，|a|＞|b|，
∴﹣b＜0，﹣c＜0，ac＜0，a﹣c＜0，a+b＜0．
∴a﹣b﹣c＜0．
故①正确；
∵++＝＝﹣1+1+1＝1，
∴②正确；
∵ac＜0，﹣b＜0，
∴ac﹣b＜0．
故③错误；
∵a﹣c＜0，a+b＜0，
∴|a﹣c|﹣|a+b|＝c﹣a+a+b＝c+b．
故④正确；
综上，错误的个数为1个．
故选：A．
【点评】本题主要考查了有理数的大小的比较，数轴，有理数的运算，绝对值的意义，利用数字在数轴上的位置确定数字的符号是解题的关键．
二、填空题（每小题4分，共20分）
9．某粮店出售的三种品牌的面粉袋上，分别标有质量为（25±0.1）kg，（25±0.2）kg，（25±0.3）kg的字样，从中任意拿出两袋，它们的质量最多相差 0.6kg ．
【分析】根据质量的范围求出质量的最大值（25+0.4）和最小值（25﹣0.4），相减即可求出答案．
解：质量最小值是25﹣0.3＝24.7，
最大值是25+0.3＝25.3，
∴25.3﹣24.7＝0.6（kg）．
故答案为：0.6kg．
【点评】本题考查了有理数的加减的应用，理解题意能求出质量的最大值和最小值是解此题的关键．
10．小江同学与小北同学约定了一种新运算：a△b＝3a﹣2b．小江同学尝试计算2△5＝3×2﹣2×5＝6﹣10＝﹣4，现在请小北同学计算2△（﹣5）＝ 16 ．
【分析】根据约定的新运算，把相应的数字代入运算即可．
解：由题意得：2△（﹣5）
＝3×2﹣2×（﹣5）
＝6+10
＝16．
故答案为：16．
【点评】本题主要考查有理数的混合运算，解答的关键是理解清楚题意，明确新运算的方式．
11．计算：20×（﹣5）＝ ﹣100 ．
【分析】采用简便方法计算，把20看做（20+），利用乘法分配律计算．
解：20×（﹣5）
＝（20+）×（﹣5）
＝20×（﹣5）+×（﹣5）
＝﹣100﹣
＝﹣100．
【点评】本题考查了有理数的乘法，解题的关键是掌握有理数混合运算的顺序和运算律的应用．
12．若代数式3x+2与代数式5x﹣10的值互为相反数，则x＝ 1
【分析】利用互为相反数之和为0列出方程，求出方程的解即可得到x的值．
解：根据题意得：3x+2+5x﹣10＝0，
移项合并得：8x＝8，
解得：x＝1，
故答案为：1
【点评】此题考查了解一元一次方程，以及相反数，熟练掌握运算法则是解本题的关键．
13．如图①是一个小正方体的侧面展开图，小正方体从如图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格，这时小正方体朝上面的字是 路 ．
【分析】根据正方体的表面展开图找出相对面，然后动手操作即可解答．
解：根据正方体表面展开图的“相间、Z端是对面”可知，
“中”与“梦”的面是相对的，
“复”与“路”的面是相对的，
“国”与“兴”的面是相对的，
根据题意可知第1格是“兴”，所以第4格是“国”；
第2格是梦”，第3格是“路”，所以第5格是“复”．
所以这时小正方体朝上面的字是“路”，
故答案为：路．
【点评】本题考查正方体的展开与折叠，掌握正方体表面展开图的特征是正确判断的前提．
三、解答题（共计48分）
14．把下列各数分别填在相应的集合内：
﹣11，4.8，73，﹣2.7，，3.14，﹣，，0．
正分数集合：{ 4.8，，3.14， …}；
负有理数集合：{ ﹣11，﹣2.7，﹣ …}；
整数集合：{ ﹣11，73，0 …}；
非正整数集合：{ ﹣11，0 …}．
【分析】根据有理数的分类逐一解答即可．
解：正分数集合：{4.8，，3.14，…}；
负有理数集合：{﹣11，﹣2.7，﹣…}；
整数集合：{﹣11，73，0…}；
非正整数集合：{﹣11，0…}．
故答案为：4.8，，3.14，；﹣11，﹣2.7，﹣；﹣11，73，0；﹣11，0．
【点评】本题考查了有理数分类，掌握有理数的分类是解题的关键．
15．计算：
（1）（﹣4）﹣（﹣2）+（﹣9）+3.5；
（2）1÷（0.75）×（﹣1）÷3×（﹣0.5）2；
（3）（﹣3）2﹣（1）3×﹣6÷；
（4）（﹣3+﹣）×（﹣36）．
【分析】（1）原式利用减法法则变形，计算即可求出值；
（2）原式先计算乘方，再利用除法法则变形，约分即可得到结果；
（3）原式先计算乘方，再乘除，最后算加减即可求出值；
（4）原式利用乘法分配律计算即可求出值．
解：（1）原式＝（﹣4）+2+（﹣9）+3.5
＝[（﹣4）+（﹣9）]+（2+3.5）
＝（﹣14）+6
＝﹣8；
（2）原式＝1××（﹣）××
＝﹣；
（3）原式＝9﹣×﹣6×
＝9﹣﹣9
＝﹣；
（4）原式＝×（﹣36）﹣3×（﹣36）+×（﹣36）﹣×（﹣36）
＝﹣18+108﹣30+21
＝81．
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
16．如图，是由6个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．
（1）直接写出这个几何体的表面积（包括底部）： 26cm2 ；
（2）请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．
【分析】（1）三视图面积和的2倍即可；
（2）利用三视图的画法画出图形即可．
解：（1）（5+4+4）×2＝26（cm2），
故答案为：26cm2；
（2）根据三视图的画法，画出相应的图形如下：
【点评】本题考查简单组合体的三视图，理解三视图的意义是正确解答问题的关键．
17．某果农把自家果园的柑橘包装后放到了网上销售．原计划每天卖10箱，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某个星期的销售情况（超额记为正，不足记为负，单位：箱）．
（1）根据记录的数据可知前五天共卖出多少箱？
（2）本周实际销售总量达到了计划数量没有？
（3）若每箱柑橘售价为80元，同时需要支出运费7元/箱，那么该果农本周总共收入多少元？
【分析】（1）将前五天的销售量相加即得结论；
（2）将表格中记录的数据相加得出结果，结果的符号表示达到或不足，结果的绝对值表示达到或不足的数量；
（3）利用本周的总收入减去总运费即得结论．
解：（1）10×5+4﹣3﹣5+7﹣8＝45 （箱），
答：根据记录的数据可知前五天共卖出45箱；
（2）4﹣3﹣5+7﹣8+21﹣6＝10＞0，
答：本周实际销售总量达到了计划数量；
（3）（10×7+10）×80﹣（10×7+10）×7＝5840（元），
答：该果农本周总共收入5840元．
【点评】此题考查正数和负数的问题，此题的关键是读懂题意，列式计算．
18．如图①是一张长为18cm，宽为12cm的长方形硬纸板．把它的四个角都剪去一个边长为xcm的小正方形，然后把它折成一个无盖的长方体盒子（如图②），请回答下列问题：
（1）折成的无盖长方体盒子的容积V＝ （18﹣2x）•（12﹣2x）•x cm3；（用含x的代数式表示即可，不需化简）
（2）请完成下表，并根据表格回答，当x取什么正整数时，长方体盒子的容积最大？
（3）从正面看折成的长方体盒子，它的形状可能是正方形吗？如果是正方形，求出x的值；如果不是正方形，请说明理由．
【分析】（1）表示出长方体盒子的长、宽、高，即可表示出体积；
（2）把x的值分别代入（1）中的代数式求值即可；
（3）若正面是正方形，说明长方体的长和高相等，列方程求解，再进行检验即可．
解：（1）由题意得，长方体盒子的长（18﹣2x）、宽（12﹣2x）、高x，因此体积为：（18﹣2x）•（12﹣2x）•x，
故答案为：（18﹣2x）•（12﹣2x）•x，
（2）把x＝2代入（18﹣2x）•（12﹣2x）•x得，（18﹣2x）•（12﹣2x）•x＝14×8×2＝224，
把x＝4代入（18﹣2x）•（12﹣2x）•x得，（18﹣2x）•（12﹣2x）•x＝10×4×4＝160，
故答案为：224，160；
（3）它的形状不可能是正方形，
当18﹣2x＝x时，即x＝6，而当x＝6时，图①的长边变为0，因此折不成长方体，故从正面看是正方形是不可能的．
【点评】考查展开与折叠，抽象出长方体的长、宽、高与原长方形的边长之间的关系是正确解答的关键．
一、填空题（每小题4分，共计20分）
19．计算：÷（）＝ ．
【分析】先计算括号内分数的加减，再将除法转化为乘法，计算乘法可得答案．
解：原式＝÷（﹣+）
＝÷
＝×
＝，
故答案为：．
【点评】本题主要考查有理数的混合运算，解题的关键是掌握有理数的混合运算顺序和运算法则．
20．已知|a|＝4且a＜0，b是绝对值最小的数，c是最大的负整数，则a+b﹣c＝ ﹣3 ．
【分析】由|a|＝4且a＜0，求a的值，b是绝对值最小的数，c是最大的负整数，求b、c的值，就得到a+b﹣c的值．
解：∵|a|＝4，
∴a＝±4．
∵a＜0，
∴a＝﹣4．
∵b是绝对值最小的数，
∴b＝0．
∵c是最大的负整数，
∴c＝﹣1．
把a＝﹣4，b＝0，c＝﹣1，代入a+b﹣c中，
∴a+b﹣c＝﹣3．
故答案为：﹣3．
【点评】本题考查了有理数的加减混合运算，绝对值的性质，掌握运算法则，求a、b、c、的值是解题关键．
21．如图为一个用正方体积木搭成的几何体的三视图，俯视图中方格上的数字表示该位置上积木累积的个数．若保证正视图和左视图成立，则a+b+c+d的最大值为 13 ．
【分析】由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状，依此即可求解．
解：由正视图第1列和左视图第1列可知a最大为3，由正视图第2列和左视图第2列可知b最大为3，由正视图第3列和左视图第1列和第2列可知c最大为4，d最大为3，
则a+b+c+d的最大值为3+3+4+3＝13．
故答案为：13．
【点评】此题考查了由三视图判断几何体，关键看学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查，用到的知识点是三视图．
22．如图，一个正方体截去一个角后，剩下的几何体有 7 个面，有 12 条棱．
【分析】观察图形，数剩下的几何体的面数和棱数即可．
解：观察图形可知：剩下的几何体有7个面，有12条棱，
故答案为：7；12．
【点评】本题考查了立体图形的认识，截面的形状，考查学生的空间观念，数出剩下的几何体的面数和棱数是解题的关键．
23．阅读下列材料，并解决后面的问题．
材料：一般地，n个相同的因数a相乘：记为．如23＝8，此时，3叫做以2为底8的对数，记为lg28（即lg28＝3）．一般地，若an＝b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为lgab（即lgab＝n）．如34＝81，则4叫做以3为底81的对数，记为lg381（即lg381＝4）．则lg24，lg216，lg264之间满足的关系式为 +＝ ．
【分析】利用题干中的定义分别计算lg24，lg216，lg264的值，利用计算结果即可得出结论．
解：∵22＝4，
∴lg24＝2，
∵24＝16，
∴lg216＝4，
∵26＝64，
∴lg264＝6，
∵2+4＝6，
∴lg24，lg216，lg264之间满足的关系式为：+＝．
故答案为：+＝．
【点评】本题主要考查了有理数的乘方，本题是阅读型题目，正确理解新定义并熟练应用是解题的关键．
二、解答题
24．若a，b互为相反数，c，d互为倒数，且|x﹣2|＝5．求：x﹣（a+b+cd）+|（a+b）﹣4|﹣（﹣cd）2021的值．
【分析】由题意得a+b＝0，cd＝1，x﹣2＝±5，继而知x＝7或x＝﹣3，再分别代入计算即可．
解：由题意知a+b＝0，cd＝1，x﹣2＝±5，
则x＝7或x＝﹣3，
当x＝7时，原式＝7﹣（0+1）+|0﹣4|﹣（﹣1）2021
＝7﹣1+4+1
＝11；
当x＝﹣3时，原式＝﹣3﹣（0+1）+|0﹣4|﹣（﹣1）2021
＝﹣3﹣1+4+1
＝1；
综上，原式的值为11或1．
【点评】本题主要考查有理数的混合运算，解题的关键是掌握有理数的混合运算顺序和运算法则．
25．观察下列等式＝1﹣，＝﹣，＝﹣，将以上三个等式两边分别相加得++＝1﹣+﹣+﹣＝1﹣＝．
（1）猜想并写出＝ ﹣ ；
（2）+++…+＝ ；
（3）探究并计算：+++…+；
（4）计算：++++++++．
【分析】（1）先根据题中所给出的等式进行猜想，写出猜想结果即可；
（2）根据（1）中的猜想计算出结果；
（3）根据乘法分配律提取，再计算即可求解；
（4）先拆项，再抵消即可求解．
解：（1）＝﹣；
故答案为：﹣；
（2）+++…+
＝1﹣+﹣+﹣+…+﹣
＝1﹣
＝；
故答案为：；
（3）+++…+
＝（+++…+）
＝（1﹣）
＝×
＝；
（4）++++++++
＝（+++…+）
＝（1﹣）
＝
＝．
【点评】本题考查的是有理数的混合运算，根据题意找出规律是解答此题的关键．
26．已知数轴上点A，O，P所表示的数分别是﹣3，0，x点P在线段AO上．
（1）请在数轴上标出A，O两点；
（2）①线段AP＝ x+3 （用含x的式子表示）
②在点P右侧的数轴上画线段PQ＝AP，当OP＝2OQ时，求x的值．
【分析】（1）根据数轴的特点数轴上标出A，O两点；
（2）①根据两点间的距离公式即可求解；
②情况一：当点Q在点O的左侧时，情况二：当点Q在点O右侧时，进行讨论即可求解．
解：（1）如图所示：
（2）①线段AP＝x+3；
②情况一：当点Q在点O的左侧时，如图：
∵AP＝PQ，
∴AQ＝2AP＝2（x+3）＝2x+6，
OQ＝OA﹣AQ＝3﹣（2x+6）＝﹣2x﹣3，
OP＝﹣x，
OP＝2OQ，
﹣x＝2（﹣2x﹣3），
x＝﹣2．
情况二：当点Q在点O右侧时，如图：
此时OQ＝AQ﹣OA＝（2x+6）﹣3＝2x+3，
OP＝2OQ，
﹣x＝2（2x+3），
．
综上，x的值为﹣2或．
故答案为：x+3．
【点评】考查了列代数式，两点间的距离和数轴，解题时，需要采用数形结合和分类应用的数学思想．
星期
一
二
三
四
五
六
日
与计划量的差值
+4
﹣3
﹣5
+7
﹣8
+21
﹣6
x/cm
1
2
3
4
5
V/cm3
160

216

80
星期
一
二
三
四
五
六
日
与计划量的差值
+4
﹣3
﹣5
+7
﹣8
+21
﹣6
x/cm
1
2
3
4
5
V/cm3
160
224
216
160
80