







数学八年级下册3 三角形的中位线优秀课件ppt
展开北师大版八年级数学下册
《6.3三角形的中位线》教学设计
课题名 | 6.3三角形的中位线 |
教学目标 | 1.知识与技能:理解三角形的中位线的概念,会区别三角形的中线;掌握三角形中位线性质. 2.过程与方法:经历探索三角形中位线性质的过程,体会转化的思想方法.通过相关问题的变式探究进一步培养学生的思维发散和创新能力. 3.情感态度和价值观:通过对三角形中位线定理的自主探究,让学生获得亲自参与探索的情感体验,从而培养学生科学分析的态度和积极的探索精神. |
教学重点 | 平行四边形判定定理的探究,运用平行四边形的判定定理解决问题. |
教学难点 | 对平行四边形判定方法的探究以及平行四边形的性质和判定的综合运用. |
教学准备 | 教师准备:课件、三角尺 学生准备:三角尺及常规用具 |
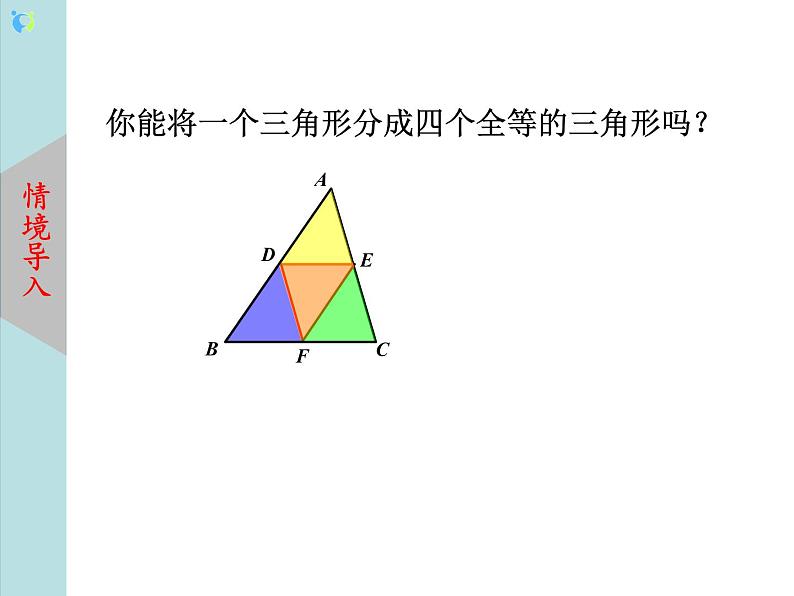
教学过程 | 一、 新课导入 情景问题:你能将一个三角形分成四个全等的三角形吗? 师生活动:教师引导学生展示课前对本问题操作的成果及其思考过程,引导学生发现连接三角形两边中点的线段的特殊性,激发学生的好奇心及进一步探究的兴趣;学生在分享过程中感受到大家得出的结果是相同的,但是思维的过程及具体的操作过程却是不同的 设计意图:通过设计这样有趣又有挑战性的动手操作题,激发学生探究欲望,也水到渠成地引出三角形的中位线的概念,同时让学生在动手操作中经历“探索---猜想---验证“的过程,发展学生合情推理及通过动手操作去初步检验猜想的合理性的能力. 二、 新知讲授 知识点一:三角形中位线的性质 连接三角形两边中点的线段叫做三角形的中位线. 符号语言: ∵ D、E分别为AB、AC的中点 ∴ DE为△ABC的中位线 已知:如图,D、E分别是△ABC的边AB、AC的中点. 求证:DE∥BC,
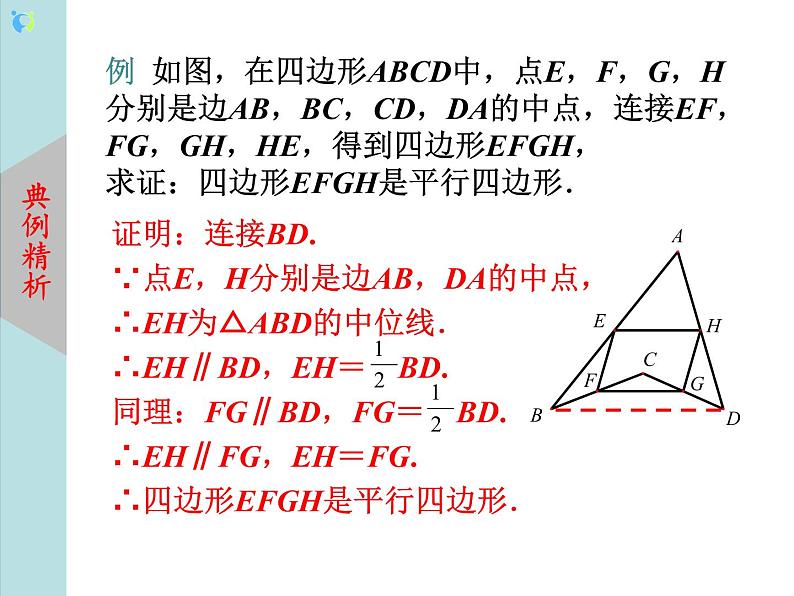
师生活动:让学生经过动手操作,给出三角形中位线的定义,既让学生得出三角形中位线的概念又让学生在无形中区分了三角形的中线和三角形中位线.有了前面的交流活动,学生要证明三角形的中位线定理思路就清晰多了,教师要引导学生正确的做出辅助线. 设计意图:几何定理的证明不但能加深学生对定理的印象及认识,同时也是进一步培养学生应用已有知识来解决新问题的一个重要契机. 例 如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE,得到四边形EFGH, 求证:四边形EFGH是平行四边形.
设计意图:通过例题,让学生对三角形中位线定理有更深入的理解;让学生会规范书写;对能应用三角形中位线定理来解决的问题形成感知. 知识点二:中点四边形 已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点. 求证:四边形EFGH是平行四边形.
顺次连接四边形各边中点所得的四边形(中点四边形)是平行四边形. 学生活动:利用课前准备好的学具动手操作、观察,完成探究活动,得出猜想命题. 设计意图:引导学生体会四边形问题转化为三角形问题解决;看到中点,联想到中位线后去构造基本的图形. 三、 知识巩固 1.如图,MN 为△ABC 的中位线,若∠ABC =61°,则∠AMN = , 若MN =12 ,则BC = .
2. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3, E,F,G,H分别是AB,BD, CD,AC的中点,则四边形EFGH的周长为( ) A.12 B.14 C.24 D.21 3. 如图,已知长方形ABCD中,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当P在BC上从B向C移动而R不动时,下列结论成立的是( ) A.线段EF的长逐渐增大 B.线段EF的长逐渐减小 C.线段EF的长不改变 D.线段EF的长先增大后减小 4. 如图,D,E,F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC 的周长为( ) A.5 B.10 C.20 D.40
5. 在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则 EF和MN的关系是__________. 6. 如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m, DE=24 m,则AB=( ) A.50 m B.48 m C.45 m D.35 m 7. (1)顺次连结平行四边形各边中点所得的四边形是 . (2)顺次连结矩形各边中点所得的四边形是 . (3)顺次连结菱形各边中点所得的四边形是 . (4)顺次连结正方形各边中点所得的四边形是 . (5)顺次连结等腰梯形各边中点所得的四边形是 . (6)顺次连结对角线相等的四边形各边中点所得的四边形是 . (7)顺次连结对角线垂直的四边形各边中点所得的四边形是 . (8)顺次连结对角线既相等又垂直的四边形各边中点所得的四边形是 . 8. 如图,在△ABC中,CD⊥AB于点D,E,F分别BC,AC的中点,连接DF,DE,EF,若△ABC的周长为6,求△DEF的周长.
四、 课堂小结 三角形的中位线: 定义:两连结三角形两边中点的线段叫做三角形的中位线.判定定理1:两组对边分别相等的四边形是平行四边形. 性质:三角形的中位线平行于第三边,且等于第三边的一半. 应用:①周长;②面积;③综合应用. |
布置作业 | 教材152页2,3题 |
板书设计 | 6.3三角形的中位线
|
教学反思 | 本节课以探究三角形中位线的性质及证明为主线开展教学活动.在三角形中位线定理探究过程中,学生先是通过动手画图、观察、测量、猜想出三角形中位线的性质,然后师生通过测量和课件演示验证猜想的正确性,再引导学生尝试构造平行四边形进行证明.经历知识的形成过程,使学生体会探究数学问题的基本方法.通过定理的探究与证明,努力培养学生分析问题和解决问题的能力,提升学生数学的思维品质. |
北师大版八年级下册3 三角形的中位线一等奖备课课件ppt: 这是一份北师大版八年级下册<a href="/sx/tb_c94894_t3/?tag_id=26" target="_blank">3 三角形的中位线一等奖备课课件ppt</a>,文件包含精选备课北师大版数学八年级下册63三角形的中位线课件pptx、精选备课北师大版数学八年级下册63三角形的中位线教案doc、精选备课北师大版数学八年级下册63三角形的中位线练习doc、精选备课北师大版数学八年级下册63三角形的中位线学案doc等4份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
初中数学北师大版八年级下册3 三角形的中位线课前预习ppt课件: 这是一份初中数学北师大版八年级下册3 三角形的中位线课前预习ppt课件,共31页。PPT课件主要包含了学习目标,导入新课,情境引入,讲授新课,合作探究,四个全等的三角形,两层含义,中位线,动画演示,DE和边BC的关系等内容,欢迎下载使用。
北师大版八年级下册3 三角形的中位线课文课件ppt: 这是一份北师大版八年级下册3 三角形的中位线课文课件ppt,共18页。PPT课件主要包含了创设情境引入新课,DE∥BC,师生互动探究新知,学以致用巩固新知,学生练习巩固新知,小结回顾反思提高,布置作业巩固所学等内容,欢迎下载使用。














