_江苏省苏州市姑苏区市区直属学校2022-2023学年九年级上学期期中数学试卷(含答案)

这是一份_江苏省苏州市姑苏区市区直属学校2022-2023学年九年级上学期期中数学试卷(含答案)，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
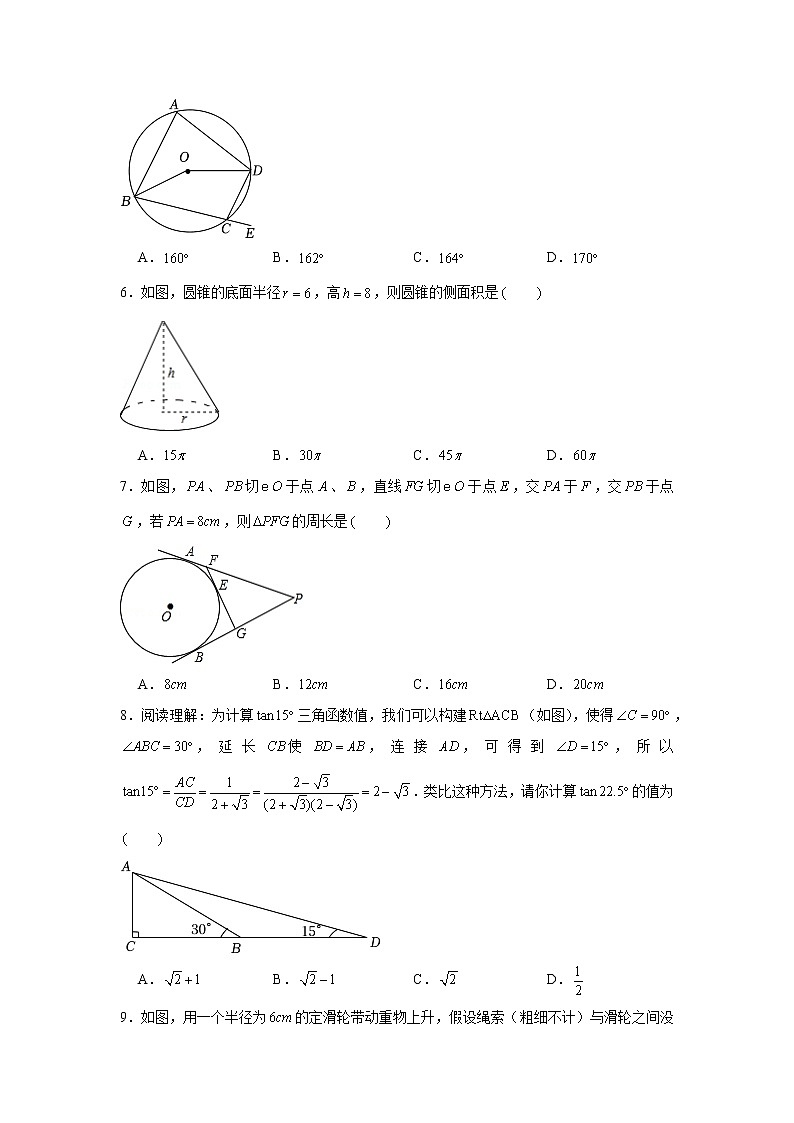
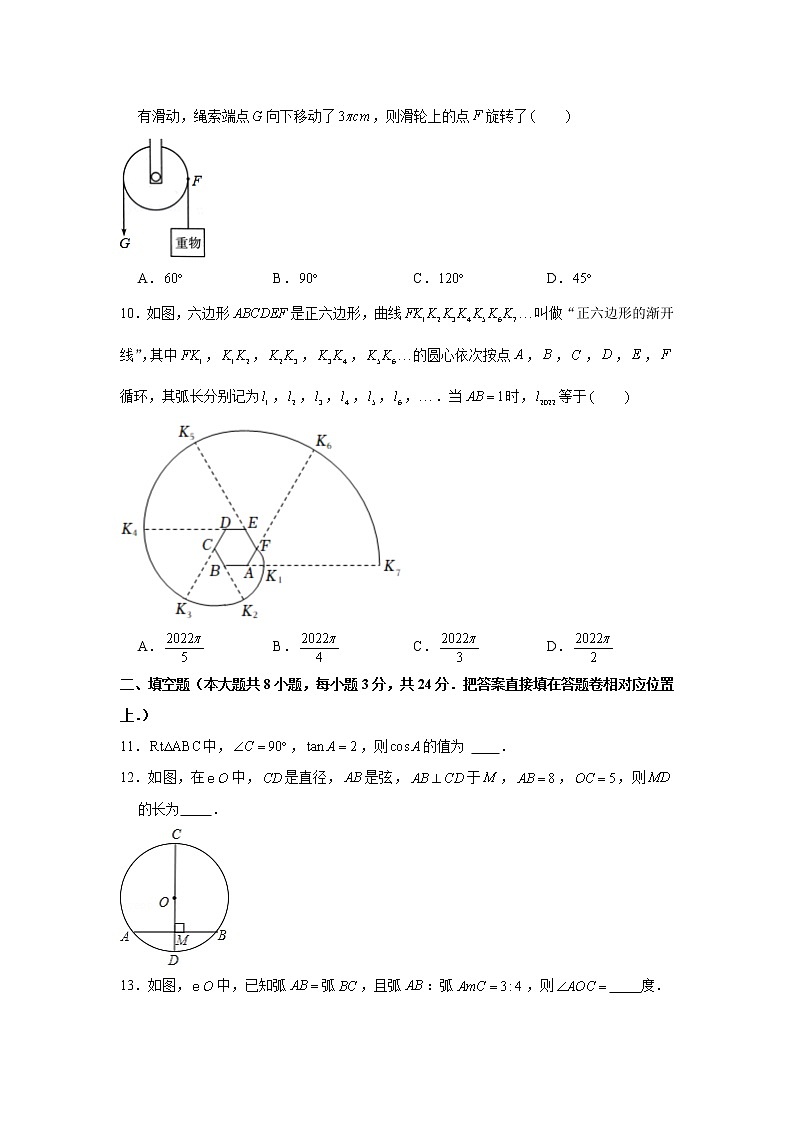
2022-2023学年江苏省苏州市姑苏区市区直属学校九年级（上）期中数学试卷一、选择题（本大题共有10小题，每小题3分，共30分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填在答题卷相应的位置上．）1．已知的半径为5，若，则点与的位置关系是　　A．点在内 B．点在上 C．点在外 D．无法判断2．下列语句中，正确的是　　A．长度相等的弧是等弧 B．在同一平面上的三点确定一个圆 C．三角形的内心是三角形三边垂直平分线的交点 D．三角形的外心到三角形三个顶点的距离相等3．如图，为了测量河岸、两点的距离，在与垂直的方向点处测得，，那么等于　　A． B． C． D．4．如图，是的直径，、是上的两点，若，则的度数为　　A． B． C． D．5．如图，是内接四边形的一个外角，若，那么的度数为　　A． B． C． D．6．如图，圆锥的底面半径，高，则圆锥的侧面积是　　A． B． C． D．7．如图，、切于点、，直线切于点，交于，交于点，若，则的周长是　　A． B． C． D．8．阅读理解：为计算三角函数值，我们可以构建（如图），使得，，延长使，连接，可得到，所以．类比这种方法，请你计算的值为　　A． B． C． D．9．如图，用一个半径为的定滑轮带动重物上升，假设绳索（粗细不计）与滑轮之间没有滑动，绳索端点向下移动了，则滑轮上的点旋转了　　A． B． C． D．10．如图，六边形是正六边形，曲线叫做“正六边形的渐开线”，其中，，，，的圆心依次按点，，，，，循环，其弧长分别记为，，，，，，．当时，等于　　A． B． C． D．二、填空题（本大题共8小题，每小题3分，共24分．把答案直接填在答题卷相对应位置上．）11．中，，，则的值为 　　．12．如图，在中，是直径，是弦，于，，，则的长为　 　．13．如图，中，已知弧弧，且弧：弧，则　 　度．14．如图，的弦、半径延长交于点，．若，则的度数是　 　．15．如图所示，三圆同心于，，于，则图中阴影部分的面积为　　．16．如图，点，，为正方形网格中的3个格点，则　　．17．如图，正方形内接于，其边长为2，则的内接正三角形的边长为　 　．18．如图，的半径为2，定点在上，动点，也在上，且满足，为的中点，当点，在圆上运动时，线段的最大值为 　　．三、解答题（本大题共9小题，共76分.把解答过程写在答题卷相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.）19．（6分）计算：（1）；（2）．20．（6分）根据下列条件解直角三角形：（1）在中，，，；（2）在中，，，．21．（8分）我们已经学习过：同弧或等弧所对的圆周角都相等，都等于该弧所对的圆心角的一半．请您就下面所给的图（1）和图（2）中，圆心与的位置关系，证明：．22．（8分）如图，公园里有三条笔直的健身步道，两两相交呈三角形，交点为、、．经测量，点在点的正东方向，点在点北偏东的方向，且在点北偏东的方向，．小明从处出发，沿着的路径散步．求小明散步的路程．23．（8分）如图1中的某种冰激凌的外包装可以视为圆锥（如图，制作这种外包装需要用如图3所示的等腰三角形材料，其中，将扇形围成圆锥时，、恰好重合，已知这种加工材料的顶角．（1）求图2中圆锥底面圆直径与母线长的比值；（2）若圆锥底面圆的直径为，求加工材料剩余部分（图3中阴影部分）的面积．（结果保留24．（8分）如图，是直径，是的中点，交的延长线于，的切线交的延长线于点．（1）求证：是的切线；（2）试探究，，三者之间的等量关系．26．（10分）如图，是的直径，点，在上，，点在的延长线上，．（1）求证：是的切线：（2）连接，若的半径长为5，，求的长．27．（12分）如图1，在平面直角坐标系中，点的坐标为，是轴正半轴上一动点，以为直径画交轴于点，连接，过点作交于点，连接，．（1）求的度数．（2）求证：．（3）如图2，连接，过点作于点，过点作交的延长线于点，设点的横坐标为．①用含的代数式表示．②记，求关于的函数表达式．
参考答案与试题解析1．【解答】解：的半径为5，若，，点与的位置关系是点在内，故选：．2．【解答】解：、在同圆或等圆中，能完全重合的弧才是等弧，故错误；、不在同一直线上的三点确定一个圆，故错误；、三角形的内心到三边的距离相等，是三条角平分线的交点，故错误；、三角形的外心是外接圆的圆心，到三顶点的距离相等，故正确；故选：．3．【解答】解：根据题意，在，有，，且，则，故选：．4．【解答】解：是的直径，，，，．故选：．5．【解答】解：，，，，，．故选：．6．【解答】解：圆锥的母线，圆锥的侧面积，故选：．7．【解答】解：根据切线长定理可得：，，；所以的周长，，，，故选：．8．【解答】解：如图：在中，，，延长使，连接，，设，则，，在中，，故选：．9．【解答】解：根据题意得：，解得：，故选：．10．【解答】解：根据题意得：，，，，按照这种规律可以得到：，所以．故选：．11．【解答】解：在中，，得为斜边．由，得．在中，，由勾股定理，得．，故答案为：．12．【解答】解：连接，，过，，，在中，，，由勾股定理得：，即，故答案为：2．13．【解答】解：弧弧，且弧：弧，弧：弧，的度数为．14．【解答】解：连接，，，，，都是等腰三角形，设的度数是，则，则在中，利用三角形的内角和是180度，可得：，解得．故答案为：．15．【解答】解：阴影部分的面积应等于圆．16．【解答】解：连接格点、因为，，所以．在中，故答案为：17．【解答】解；连接、、，作于，四边形是正方形，，，是直径，，，，，是等边三角形，，在中，，，，，．故答案为．18．【解答】解：如图，连接，，，延长到，使得，连接．，，，，当的值最大时，的值最大，，，是等边三角形，，，，，，当、、共线时，最大，的最大值为，的最大值为．故答案为：．19．【解答】解：（1）原式；（2）原式．20．【解答】解：（1），，，，，，，；（2）在中，，，，，，，，，，．21．【解答】证明：（1）如图（1），延长交于点，连接，则（同弧或等弧所对的圆周角都相等），，，（三角形的一个外角等于与它不相等的两个内角的和），，即； （2）如图（2），延长交于点，连接，则（同弧或等弧所对的圆周角都相等），，，（三角形的一个外角等于与它不相邻的两个内角的和），，即．22．【解答】解：如图，作交的延长线于．在中，，，，，在中，，，，，小明散步的路程：23．【解答】解：（1）根据题意得，，与母线长的比值为；（2），，，而，，．答：加工材料剩余部分的面积为．24．【解答】（1）证明：如图1，连接，，，是直径，，于，，，，点是的中点，，，又，垂直平分，，，是的切线；（2），理由如下：如图2，连接，由（1）知，，，为直径，，于，，，，，．26．【解答】（1）证明：连接，则，又，，，，，又是直径，是的半径；与相切；（2）解：设，，，，在中，，，，，，，，，，由（1）知，，，，，，，，，故的长为．27．【解答】解：（1）由点的坐标知，，则，，，则，则，的度数为； （2），，，； （3）①，，由点的坐标知，，则，点的坐标为，则，，即，则；②过点作交的延长线于点，连接，，故点是的中点，，故是的中位线，则，由（1）知，则，，，，，，，．声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2022/11/23 19:22:56；用户：陈文祺；邮箱：15395952626；学号：38764849