北师大版八年级下册4 多边形的内角与外角和教课课件ppt

课题名

6.4多边形的内角和与外角和第2课时

教学目标

1.知识与技能：掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题

2.过程与方法：经历探索并掌握“多边形外角和等于360°”的过程,进一步发展合情推理能力.

3.情感态度和价值观：在探究多边形外角和公式的过程中,发展学生的合情推理意识和主动探究习惯,体会数学与现实生活的紧密联系、培养学生小组合作交流意识,树立和谐的团队精神.

教学重点

多边形外角和定理的探索和应用．

教学难点

灵活运用公式解决简单的实际问题．

教学准备

教师准备：课件、三角尺

学生准备：三角尺及常规用具

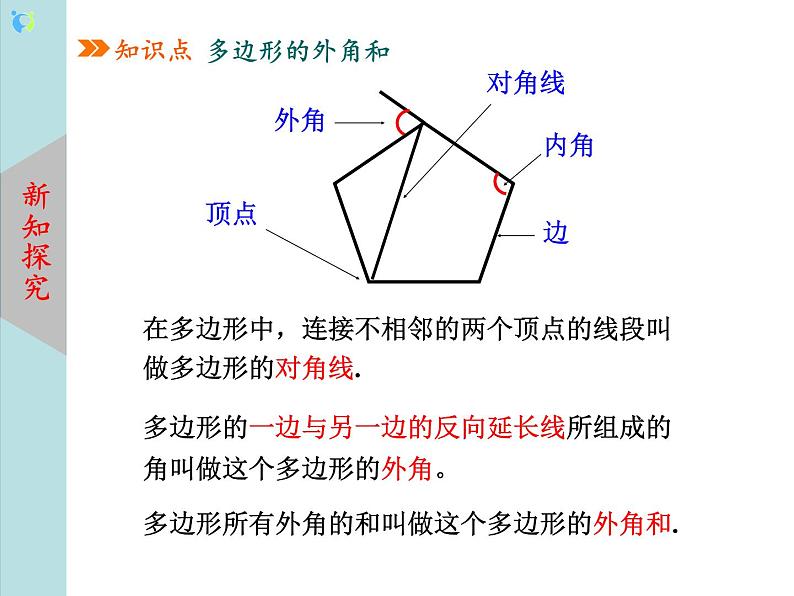
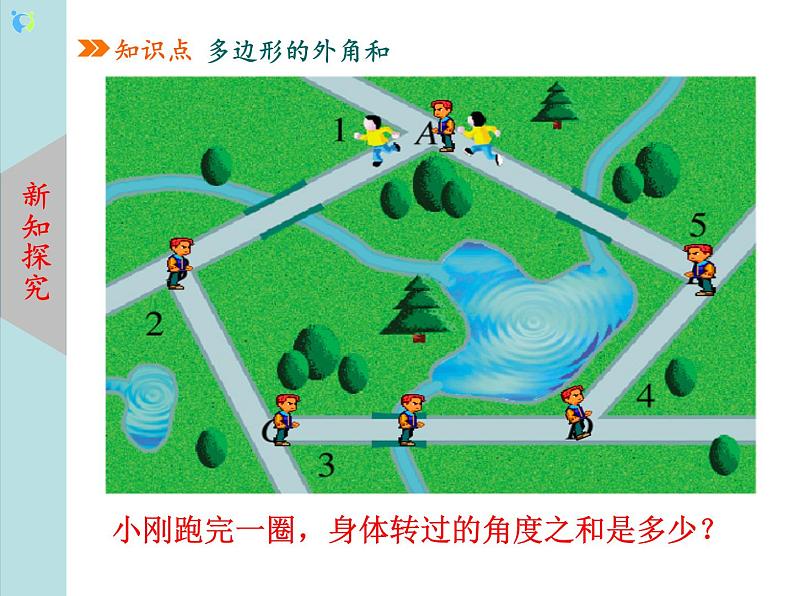
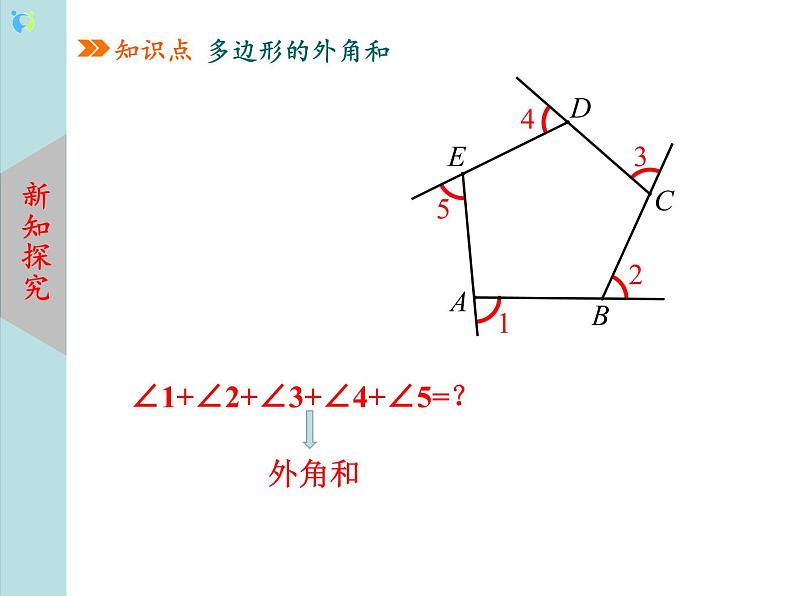
教学过程

一、    新课导入

回顾旧知：1.多边形的内角和公式是什么?

2.正n边形的内角怎么计算？

设计意图：为新知探究做铺垫.

二、    新知讲授

知识点：多边形的外角和

1.基本概念认知：在多边形中，连接不相邻的两个顶点的线段叫做多边形的对角线.

多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。

多边形所有外角的和叫做这个多边形的外角和.

2.探究新知：(多媒体演示)小明沿一个五边形广场周围的小路,按逆时针方向跑步.如                (1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?

(2)他每跑完一圈,身体转过的角度之和是多少?

(3)由此,你能求出∠1+∠2+∠3+∠4+∠5的结果吗?你是怎样得到的?

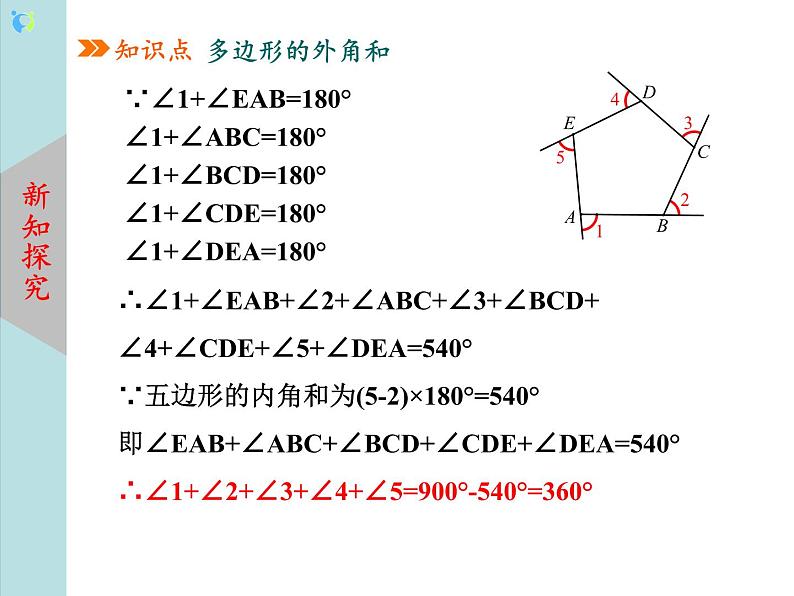
方法一:以小明自身转过的度数计算,转过一周,刚好是360°;

方法二:用量角器量出度数后计算;

方法三:把各个外角都剪出来,再拼在一起,类似验证三角形内角和的方法;

方法四:利用内角与相邻的外角互补的关系推理得出:

∵∠1+∠EAB=180°,∠2+∠ABC=180°,∠3+∠BCD=180°,∠4+∠CDE=180°,∠5+∠DEA=180°,

∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠DEA=900°.

∵五边形的内角和为(5-2)×180°=540°,

即∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°,

∴∠1+∠2+∠3+∠4+∠5=900°-540°=360°.

问题引申:

1.如果广场的形状是六边形,那么还有类似的结论吗?

2.如果广场的形状是八边形呢?

外角和定理：多边形的外角和都等于360°

设计意图：利用生活情境,设计问题,激发学生的兴趣和积极性,同时给学生一定的思考空间,很好地训练学生的合作交流的意识和分析问题、解决问题的能力.通过问题的解决和延伸,引发学生自主思考,由特殊到一般,培养学生解决问题的逻辑思维能力,也为多边形外角和的得出做好铺垫.

例 一个多边形的内角和等于它的外角和的3倍，它是几边形？

三、知识巩固

1. 五边形的外角和等于(　　)

A．180°                           B．360° 

C．540°                           D．720°

2.如果正n边形每一个内角等于与它相邻外角的2倍，则n的值是(　　)

A．4           B．5       C．6         D．7

3.如图，小华从点A出发，沿直线前进10 m后向左转24°，再沿直线前进10 m，又向左转24°……照这样走下去，他第一次回到出发地点A时，一共走的路程是（      ）

A. 140 m        B. 150 m    C. 160 m        D. 240 m

4．多边形的内角和为外角和的4倍，这个多边形是（　　）

A．八边形        B．九边形      C．十边形        D．十一边形

5．正多边形的一个外角等于36°，则该多边形是正(　　)

A．八边形      B．九边形  C．十边形      D．十一边形

6. 一个正多边形的内角和是540゜，则这个正多边形的每一个外角等于（    ）

A．60゜           B．72゜           C．90゜           D．108゜

7. 一个多边形的内角和与外角和的差为1260°，求它的边数．

8. 若一个多边形的边数增加1,则这个多边形的内角和与外角和增加的度数之和是(　　)

A.60°  B.90°  C.180°  D.360°

9. 正八边形中,每个内角与每个外角的度数之比为(　　)

A.1∶3  B.1∶2  C.2∶1  D.3∶1

10. 如图,在五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是五边形的外角,则

∠1+∠2+∠3=　　　　. 

11. (1)如图①,已知△ABC为直角三角形，∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2

等于              度;

(2)如图②,已知在△ABC中,∠A=40°,剪去∠A后成了四边形,则∠1+∠2等于              度.

(3)根据(1)与(2)的求解过程，请你归纳猜想∠1+∠2与∠A的关系是              ;

(4)如图③,若没有剪掉∠A,而是把它折成如图所示的形状,试探究∠1+∠2与∠A的关系，并说明理由.

拓展练习：12. 如图,求则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为      .

13. 一副三角尺如图所示摆放，则∠α与∠β的数量关系为(　　)

A．∠α＋∠β＝180° 

B．∠α＋∠β＝225°

C．∠α＋∠β＝270° 

D．∠α＝∠β

四、课堂小结

1．多边形的内角和等于(n－2)·180°，多边形的外角和等于360°.

2．多边形的边数与内角和、外角和的关系：

(1)n边形的内角和等于(n－2)·180°(n≥3，n是正整数)，可见多边形内角和与边数n有关，每增加1条边，内角和增加180°.

(2)多边形的外角和等于360°，与边数的多少无关.

3.正n边形：正n边形的内角的度数为，外角的度数为

布置作业

教材157页1,2,3题

板书设计

        6.4多边形的内角和与外角和(第2课时)

多边形的内角和等于(n－2)·180°；

多边形的外角和等于360°.

教学反思

本节课的设计突出对多边形的外角和公式的探究与推导过程，探究过程既有类比前一节课的方法，又有承接多边形内角和的新方法；既是新知识的学习过程，又是旧知识的拓展过程．相信这样的设计一定能够达到教学目标的三个维度的要求．另外，可以考虑增加一些课堂中的习题量，以帮助学生巩固新知识．