2022年人教版浙江省丽水市中考数学试卷

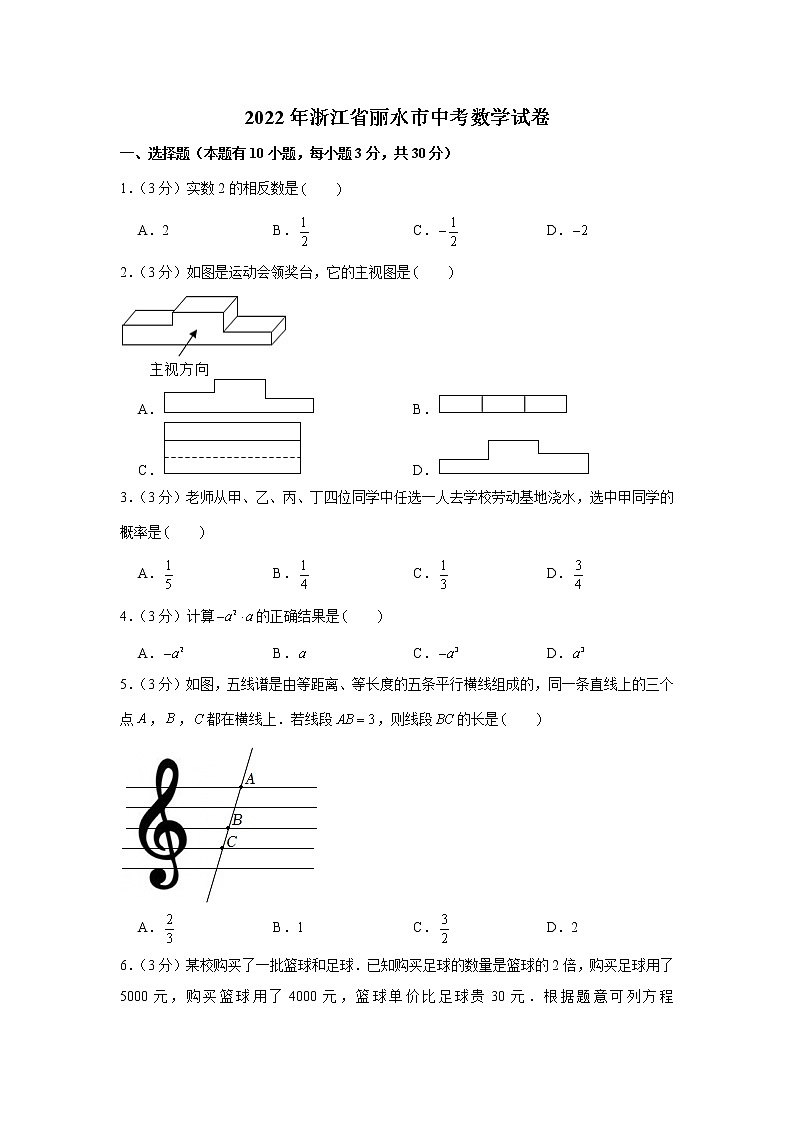
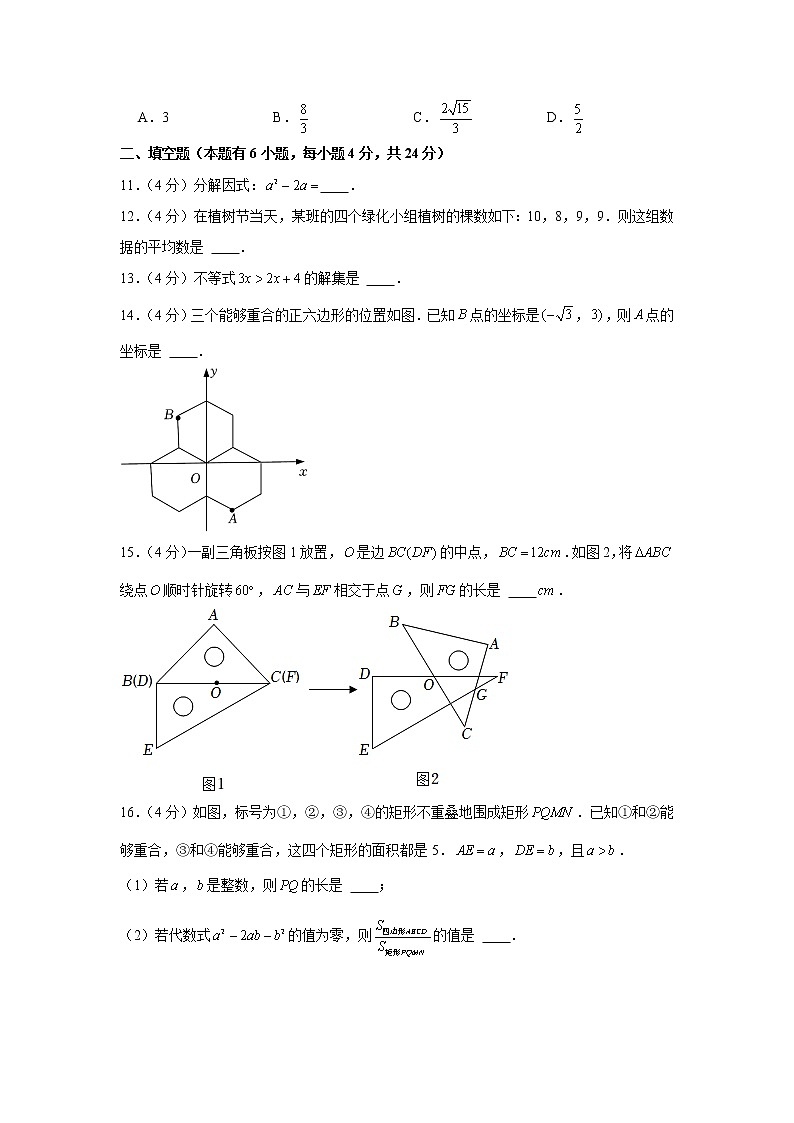
2022年浙江省丽水市中考数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．（3分）实数2的相反数是　　A．2 B． C． D．2．（3分）如图是运动会领奖台，它的主视图是　　A． B． C． D．3．（3分）老师从甲、乙、丙、丁四位同学中任选一人去学校劳动基地浇水，选中甲同学的概率是　　A． B． C． D．4．（3分）计算的正确结果是　　A． B． C． D．5．（3分）如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点，，都在横线上．若线段，则线段的长是　　A． B．1 C． D．26．（3分）某校购买了一批篮球和足球．已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元．根据题意可列方程，则方程中表示　　A．足球的单价 B．篮球的单价 C．足球的数量 D．篮球的数量7．（3分）如图，在中，，，分别是，，的中点．若，，则四边形的周长是　　A．28 B．14 C．10 D．78．（3分）已知电灯电路两端的电压为，通过灯泡的电流强度（A）的最大限度不得超过．设选用灯泡的电阻为，下列说法正确的是　　A．至少 B．至多 C．至少 D．至多9．（3分）某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为，高为，则改建后门洞的圆弧长是　　A． B． C． D．10．（3分）如图，已知菱形的边长为4，是的中点，平分交于点，交于点．若，则的长是　　A．3 B． C． D．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）分解因式：　　．12．（4分）在植树节当天，某班的四个绿化小组植树的棵数如下：10，8，9，9．则这组数据的平均数是 　　．13．（4分）不等式的解集是 　　．14．（4分）三个能够重合的正六边形的位置如图．已知点的坐标是，，则点的坐标是 　　．15．（4分）一副三角板按图1放置，是边的中点，．如图2，将绕点顺时针旋转，与相交于点，则的长是 　　．16．（4分）如图，标号为①，②，③，④的矩形不重叠地围成矩形．已知①和②能够重合，③和④能够重合，这四个矩形的面积都是5．，，且．（1）若，是整数，则的长是 　　；（2）若代数式的值为零，则的值是 　　．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分，各小题都必须写出解答过程）17．（6分）计算：．18．（6分）先化简，再求值：，其中．19．（6分）某校为了解学生在“五一”小长假期间参与家务劳动的时间（小时），随机抽取了本校部分学生进行问卷调查．要求抽取的学生在，，，，五个选项中选且只选一项，并将抽查结果绘制成如下两幅不完整的统计图，请根据图中信息回答问题：（1）求所抽取的学生总人数；（2）若该校共有学生1200人，请估算该校学生参与家务劳动的时间满足的人数；（3）请你根据调查结果，对该校学生参与家务劳动时间的现状作简短评述．20．（8分）如图，在的方格纸中，点，，均在格点上，试按要求画出相应格点图形． （1）如图1，作一条线段，使它是向右平移一格后的图形；（2）如图2，作一个轴对称图形，使和是它的两条边；（3）如图3，作一个与相似的三角形，相似比不等于1．21．（8分）因疫情防控需要，一辆货车先从甲地出发运送防疫物资到乙地，稍后一辆轿车从甲地急送防疫专家到乙地．已知甲、乙两地的路程是，货车行驶时的速度是．两车离甲地的路程与时间的函数图象如图．（1）求出的值；（2）求轿车离甲地的路程与时间的函数表达式；（3）问轿车比货车早多少时间到达乙地？22．（10分）如图，将矩形纸片折叠，使点与点重合，点落在点处，折痕为．（1）求证：；（2）若，，求的长．23．（10分）如图，已知点，，，在二次函数的图象上，且．（1）若二次函数的图象经过点．①求这个二次函数的表达式；②若，求顶点到的距离；（2）当时，二次函数的最大值与最小值的差为1，点，在对称轴的异侧，求的取值范围．24．（12分）如图，以为直径的与相切于点，点在左侧圆弧上，弦交于点，连结，．点关于的对称点为，直线交于点，交于点．（1）求证：；（2）当点在上，连结交于点，若，求的值；（3）当点在射线上，，以点，，，为顶点的四边形中有一组对边平行时，求的长．
2022年浙江省丽水市中考数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．（3分）实数2的相反数是　　A．2 B． C． D．【分析】相反数的概念：只有符号不同的两个数叫做互为相反数．【解答】解：实数2的相反数是．故选：．2．（3分）如图是运动会领奖台，它的主视图是　　A． B． C． D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看，可得如下图形：故选：．3．（3分）老师从甲、乙、丙、丁四位同学中任选一人去学校劳动基地浇水，选中甲同学的概率是　　A． B． C． D．【分析】利用事件概率的意义解答即可．【解答】解：老师从甲、乙、丙、丁四位同学中任选一人去学校劳动基地浇水，事件的等可能性有4种，选中甲同学的可能性有一种，选中甲同学的概率是，故选：．4．（3分）计算的正确结果是　　A． B． C． D．【分析】同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加．据此判断即可．【解答】解：，故选：．5．（3分）如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点，，都在横线上．若线段，则线段的长是　　A． B．1 C． D．2【分析】过点作平行横线的垂线，交点所在的平行横线于，交点所在的平行横线于，根据平行线分线段成比例定理列出比例式，计算即可．【解答】解：过点作平行横线的垂线，交点所在的平行横线于，交点所在的平行横线于，则，即，解得：，故选：．6．（3分）某校购买了一批篮球和足球．已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元．根据题意可列方程，则方程中表示　　A．足球的单价 B．篮球的单价 C．足球的数量 D．篮球的数量【分析】设篮球的数量为个，足球的数量是个，列出分式方程解答即可．【解答】解：设篮球的数量为个，足球的数量是个．根据题意可得：，故选：．7．（3分）如图，在中，，，分别是，，的中点．若，，则四边形的周长是　　A．28 B．14 C．10 D．7【分析】根据三角形中位线定理解答即可．【解答】解：，，分别是，，的中点，，、分别为、中点，，四边形的周长为：，故选：．8．（3分）已知电灯电路两端的电压为，通过灯泡的电流强度（A）的最大限度不得超过．设选用灯泡的电阻为，下列说法正确的是　　A．至少 B．至多 C．至少 D．至多【分析】利用已知条件列出不等式，解不等式即可得出结论．【解答】解：电压一定时，电流强度（A）与灯泡的电阻为成反比例，．已知电灯电路两端的电压为，．通过灯泡的电流强度（A）的最大限度不得超过，，．故选：．9．（3分）某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为，高为，则改建后门洞的圆弧长是　　A． B． C． D．【分析】先作出合适的辅助线，然后根据题意和图形，可以求得优弧所对的圆心角的度数和所在圆的半径，然后根据弧长公式计算即可．【解答】解：连接，，和相交于点，则为圆心，如图所示，由题意可得，，，，，，，，，，优弧所对的圆心角为，改建后门洞的圆弧长是：，故选：．10．（3分）如图，已知菱形的边长为4，是的中点，平分交于点，交于点．若，则的长是　　A．3 B． C． D．【分析】方法一：过点作于点，过点作于点，根据，可得，所以，然后证明是的垂直平分线，可得，设，根据，进而可以解决问题．方法二：作垂直于，延长和交于点由已知可得，所以设，则，，由三角形相似于三角形即可得结论．【解答】解：方法一，如图，过点作于点，过点作于点，菱形的边长为4，，，，，是的中点，，，是的垂直平分线，，平分，，，，，，设，，，，，，，，，解得，则的长是．方法二：如图，作垂直于，延长和交于点，由已知可得，所以，设，则，，由，，，解得．故选：．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）分解因式：　　．【分析】观察原式，找到公因式，提出即可得出答案．【解答】解：．故答案为：．12．（4分）在植树节当天，某班的四个绿化小组植树的棵数如下：10，8，9，9．则这组数据的平均数是 　9　．【分析】算术平均数：对于个数，，，，则就叫做这个数的算术平均数．【解答】解：这组数据的平均数是．故答案为：9．13．（4分）不等式的解集是 　　．【分析】先移项，再合并同类项即可．【解答】解：，，，故答案为：．14．（4分）三个能够重合的正六边形的位置如图．已知点的坐标是，，则点的坐标是 　，　．【分析】根据正六边形的性质可得点和点关于原点对称，进而可以解决问题．【解答】解：因为点和点关于原点对称，点的坐标是，，所以点的坐标是，，故答案为：，．15．（4分）一副三角板按图1放置，是边的中点，．如图2，将绕点顺时针旋转，与相交于点，则的长是 　　．【分析】设与交于点，根据旋转的性质证明，可得，利用含30度角的直角三角形可得，，然后证明的等腰直角三角形，可得，进而可以解决问题．【解答】解：如图，设与交于点，是边的中点，．如图2，．将绕点顺时针旋转，，，，，，，，，．故答案为：．16．（4分）如图，标号为①，②，③，④的矩形不重叠地围成矩形．已知①和②能够重合，③和④能够重合，这四个矩形的面积都是5．，，且．（1）若，是整数，则的长是 　任意正整数　；（2）若代数式的值为零，则的值是 　　．【分析】（1）直接根据线段的差可得结论；（2）先把当常数解方程：，（负值舍），根据四个矩形的面积都是5表示小矩形的宽，最后计算面积的比，化简后整体代入即可解答．【解答】解：（1）由图可知：，，是整数，，的长是任意正整数；故答案为：任意正整数；（2），，，（负值舍），四个矩形的面积都是5．，，，，则．故答案为：．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分，各小题都必须写出解答过程）17．（6分）计算：．【分析】分别根据算术平方根的定义，任何非零数的零次幂等于1以及负整数指数幂的意义计算即可．【解答】解：原式．18．（6分）先化简，再求值：，其中．【分析】先根据平方差公式和单项式乘多项式的运算法则化简，再把代入计算即可．【解答】解：，当时，原式．19．（6分）某校为了解学生在“五一”小长假期间参与家务劳动的时间（小时），随机抽取了本校部分学生进行问卷调查．要求抽取的学生在，，，，五个选项中选且只选一项，并将抽查结果绘制成如下两幅不完整的统计图，请根据图中信息回答问题：（1）求所抽取的学生总人数；（2）若该校共有学生1200人，请估算该校学生参与家务劳动的时间满足的人数；（3）请你根据调查结果，对该校学生参与家务劳动时间的现状作简短评述．【分析】（1）用类别的人数除以类别所占百分比即可；（2）用1200乘所占比例即可；（3）根据统计图的数据解答即可．【解答】解：（1）（人，故所抽取的学生总人数为50人；（2）（人，答：估算该校学生参与家务劳动的时间满足的人数为240人；（3）由题意可知，该校学生在“五一”小长假期间参与家务劳动时间在占最多数，中位数位于这一组（答案不唯一）．20．（8分）如图，在的方格纸中，点，，均在格点上，试按要求画出相应格点图形． （1）如图1，作一条线段，使它是向右平移一格后的图形；（2）如图2，作一个轴对称图形，使和是它的两条边；（3）如图3，作一个与相似的三角形，相似比不等于1．【分析】（1）把点、向右作平移1个单位得到；（2）作点关于的对称点即可；（3）延长到使，延长到点使，则满足条件．【解答】解：（1）如图1，为所作；（2）如图2，（3）如图3，为所作．21．（8分）因疫情防控需要，一辆货车先从甲地出发运送防疫物资到乙地，稍后一辆轿车从甲地急送防疫专家到乙地．已知甲、乙两地的路程是，货车行驶时的速度是．两车离甲地的路程与时间的函数图象如图．（1）求出的值；（2）求轿车离甲地的路程与时间的函数表达式；（3）问轿车比货车早多少时间到达乙地？【分析】（1）根据路程、时间、速度三者之间的关系即可解决问题；（2）设直线的表达式为，然后利用待定系数法求一次函数解析式解答即可解决问题；（3）根据时间路程速度分别求出货车与小轿车到达终点的时间，即可解决问题．【解答】解：（1）货车的速度是，；（2）由图象可得点，，设直线的表达式为，把，代入得：，解得，；（3）由图象可得货车走完全程需要，货车到达乙地需，，，解得，两车相差时间为，货车还需要才能到达，即轿车比货车早到达乙地．22．（10分）如图，将矩形纸片折叠，使点与点重合，点落在点处，折痕为．（1）求证：；（2）若，，求的长．【分析】（1）根据证明两个三角形全等即可；（2）如图，过点作于，由勾股定理计算，设，在中，由勾股定理得：，列方程可解答．【解答】（1）证明：四边形是矩形，，，由折叠得：，，，，，，在和中，，；（2）解：如图，过点作于，，，在中，由勾股定理得：，设，由（1）知：，，，由折叠得：，，，在中，由勾股定理得：，，，．23．（10分）如图，已知点，，，在二次函数的图象上，且．（1）若二次函数的图象经过点．①求这个二次函数的表达式；②若，求顶点到的距离；（2）当时，二次函数的最大值与最小值的差为1，点，在对称轴的异侧，求的取值范围．【分析】（1）①把点代入二次函数的解析式求出即可；②判断出，关于抛物线的对称轴对称，求出点的纵坐标，可得结论；（2）分两种情形：若，在对称轴的异侧，，若，在对称轴的异侧，，，分别求解即可．【解答】解：（1）①二次函数经过，，，二次函数的解析式为； ②，，关于抛物线的对称轴对称，对称轴是直线，且，，，当时，，当时，顶点到的距离； （2）若，在对称轴的异侧，，，，，，，函数的最大值为，最小值为，，，，．若，在对称轴的异侧，，，，，函数的最大值为，最小值为，，，，．综上所述，．24．（12分）如图，以为直径的与相切于点，点在左侧圆弧上，弦交于点，连结，．点关于的对称点为，直线交于点，交于点．（1）求证：；（2）当点在上，连结交于点，若，求的值；（3）当点在射线上，，以点，，，为顶点的四边形中有一组对边平行时，求的长．【分析】（1）根据等角的余角相等证明即可；（2）证明，推出，可得结论；（3）分四种情形：如图1中，当时，如图2中，当时，如图3中，当时，如图4中，当时，分别求解即可．【解答】（1）证明：是的切线，，，，关于对称，，点在上，，，，，； （2）解：是直径，，，，，，，，，，，，，； （3）解：如图1中，当时，连接，．设，则，，，，，，，，，，，，，，，，．如图2中，当时，连接，设交点．设，，，，，，，，，，，是等腰直角三角形，，，，；如图3中，当时，连接，．设，，，，，，，，，，，，，．如图4中，当时，连接，，．设，，，，，，，由，，，，，，．综上所述，满足条件的的长为或或或，声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/6/29 6:53:07；用户：柯瑞；邮箱：ainixiaoke00@163.com；学号：500557