河南省沈丘县2022-2023学年八年级（上）数学期末模拟测试（含答案及详解）

这是一份河南省沈丘县2022-2023学年八年级（上）数学期末模拟测试（含答案及详解），共17页。试卷主要包含了选择题等内容，欢迎下载使用。
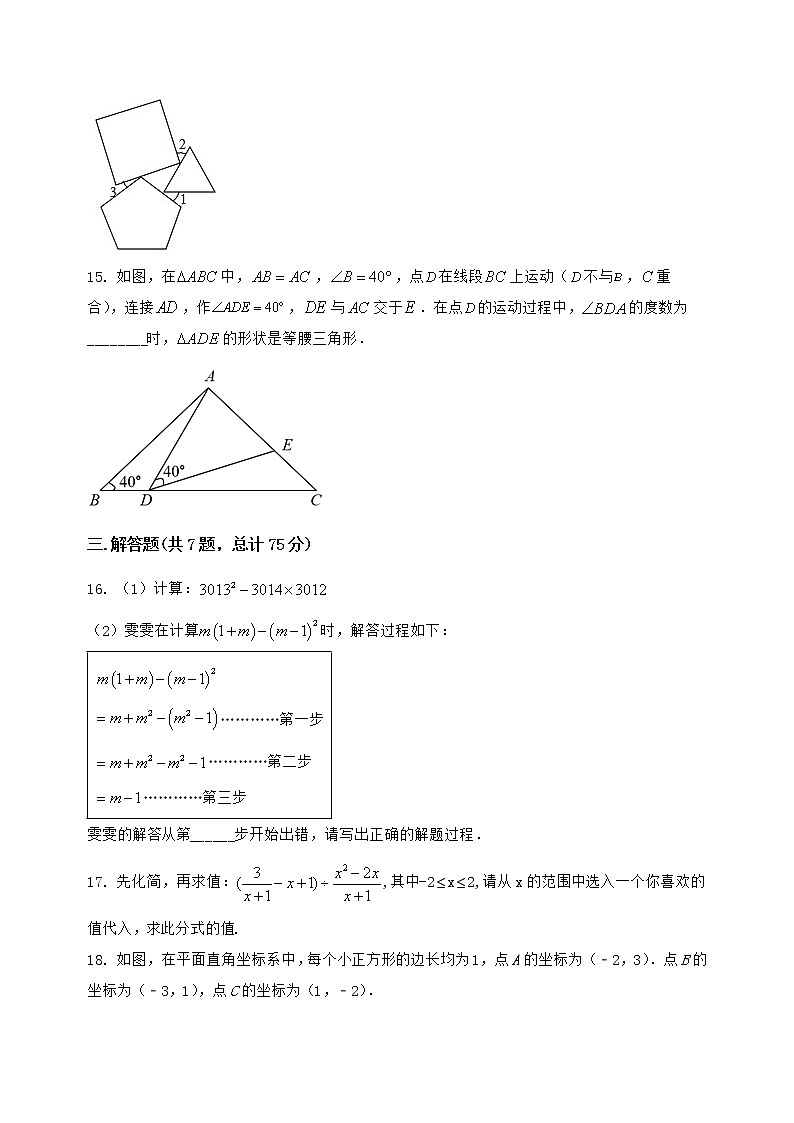
沈丘县2022-2023学年八年级（上）数学期末模拟测试一、选择题（本题共10个小题，每小题3分，共 30分。下列各题，每小题只有一个选项符合题意。）1. 下列防疫的图标中是轴对称图形的是（    ）A.  B.  C.  D. 2. 冠状病毒是一个大型病毒家族，借助电子显微镜，我们可以看到这些病毒直径约为125纳米（1纳米米），125纳米用科学记数法表示等于（    ）A. 米 B. 米 C. 米 D. 米3. 计算(4a3  12a2b  8a3b2) ÷ (4a2)的结果是（    ）A. a  3b  2ab2 B. a2 3b  2ab C. a  2ab D. 1.5a  3b4. 下列从左到右的运算是因式分解的是（　　）A. 2x2﹣2x﹣1=2x（x﹣1）﹣1 B. 4a2+4a+1=（2a+1）2C. （a+b）（a﹣b）=a2﹣b2 D. x2+y2=（x+y）2﹣2xy5. 已知三角形的两边长分别为6，11，那么第三边的长可以是（　　）A. 3 B. 4 C. 5 D. 66. 下列各式中，正确的是(　　)A. B. C. D. 7. 计算a﹣2b2•（a2b﹣2）﹣2正确的结果是（   ）A.  B.  C. a6b6 D. 8. 如果把分式中的，都扩大3倍，那么分式的值（   ）A. 扩大3倍 B. 不变 C. 缩小3倍 D. 扩大9倍9. 如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为(　　)A. 2 B.  C. 4 D. 10. 如图，在中，，，点，分别是，上的动点，将沿直线翻折，点的对点恰好落在边上，若是等腰三角形，那么的度数为（  ）A. 或 B. 或C. ，或 D. ，或二.填空题(共5题，总计 15分)11. 已知点与点关于轴对称，则的值为_________．12. 在△ABC中，2∠B＝∠A+∠C，∠A＝30°，最长边为6cm，则最短边的长为 _____cm．13. 若x2＋2mx＋9是一个完全平方式，则m的值是_______14. 将等边三角形、正方形、正五边形按如图所示的位置摆放，如果，，那么的度数等于________．15. 如图，在中，，，点在线段上运动（不与，重合），连接，作，与交于．在点的运动过程中，的度数为________时，的形状是等腰三角形．三.解答题(共7题，总计75分)16. （1）计算：（2）雯雯在计算时，解答过程如下：…………第一步…………第二步…………第三步雯雯的解答从第______步开始出错，请写出正确的解题过程．17. 先化简，再求值：,其中-2x2,请从x的范围中选入一个你喜欢的值代入，求此分式的值.18. 如图，在平面直角坐标系中，每个小正方形的边长均为1，点A的坐标为（﹣2，3）．点B的坐标为（﹣3，1），点C的坐标为（1，﹣2）．（1）作出△ABC关于y轴对称的△A'B'C'．其中A'，B'，C'分别是A，B，C的对应点，不要求写作法；（2）在x轴上找一点P，使得PB+PA的值最小．（不要求写作法）19. 如图，已知△ABC．（1）用直尺和圆规按下列要求作图：①作△ABC的角平分线AD；②作∠CBE＝∠ADC，BE交CA的延长线于点E；③作AF⊥BE，垂足为F．（2）直接判断图中EF与BF的数量关系．20. （1）若，求的值；（2）请直接写出下列问题的答案：①若，则___________；②若，则__________．21. 刘峰和李明相约周末去科技馆看展览，根据他们的谈话内容，试求李明乘公交车、刘峰骑自行车每小时各行多少千米？刘峰：我查好地图了，你看看李明：好的，我家门口的公交车站，正好有一趟到科技馆那站停的车，我坐明天的车．刘峰：从地图上看，我家到科技馆的距离比你家近10千米，我就骑自行车去了．李明：行，根据我的经验，公交车的速度一般是你骑自行车速度的3倍，那你明天早上点从家出发，如顺利，咱俩同时到达．22. 课堂上，老师提出了这样一个问题：如图1，在中，平分交于点D，且．求证：．小明的方法是：如图2，在上截取，使，连接，构造全等三角形来证明结论．（1）小天提出，如果把小明方法叫做“截长法”，那么还可以用“补短法”通过延长线段构造全等三角形进行证明．辅助线的画法是：延长至F，使_________，连接．请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；（2）小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：如图3，点D在的内部，，，分别平分，，，且．求证：．请你解答小芸提出的这个问题；（3）小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：如果在中，，点D在边上，，那么平分．小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．
沈丘县2022-2023学年八年级（上）数学期末模拟测试参考答案及解析一.选择题 1.【答案】：C【解析】：解：轴对称图形定义：把一个图形沿某条直线对折，对折后直线两旁的部分能完全重合．发现A，B，D都不符合定义，所以A，B，D都错误，只有C符合，所以C正确．故答案为C．2.【答案】：A【解析】：解：125纳米=125×10-9米=米，故选：A．2.【答案】：A【解析】：解：(4a3  12a2b  8a3b2) ÷ (4a2).故选A4.【答案】：B【解析】：解：A、没把一个多项式转化成几个整式积的形式，故本选项错误；
B、把一个多项式转化成几个整式积的形式，故本选项正确；
C、是整式的乘法，故本选项错误；
D、没把一个多项式转化成几个整式积的形式，故本选项错误；
故选：B．5.【答案】：D【解析】：设第三边长为x，由题意得：11﹣6＜x＜11+6，解得：5＜x＜17．故选D．6.【答案】：B【解析】：解：A、 ，错误；B、 ，正确；C、 ，错误；D、 ，错误．故选：B．7.【答案】：B【解析】：原式＝，故选B.【点睛】本题考查了幂的混合运算，掌握幂的运算法则是解题的关键．8.【答案】：B【解析】：．故选：B．【点睛】本题考查了分式的性质，分式的分子分母都乘以或除以同一个不为0的整式，分式的值不变．9.【答案】：C【解析】：解：∵P是∠AOB角平分线上的一点，∠AOB=60°，∴∠AOP=∠AOB=30°，∵PD⊥OA，M是OP的中点，DM=4cm，∴OP=2DM=8，∴PD=OP=4，∵点C是OB上一个动点，∴PC的最小值为P到OB距离，∴PC的最小值=PD=4．故选C10.【答案】：D【解析】：，，，分三种情况讨论：①当时，如图：，；②当时，如图：，；③当时，如图：，；综上所述，为或或，故选：D．二. 填空题11.【答案】： -1【解析】：点与点关于轴对称，，，∴，故答案为：．12.【答案】：3【解析】：解：在△ABC中，∵∠A+∠B+∠C＝180°，2∠B＝∠A+∠C，∴∠B＝60°．∴∠C＝180°﹣∠A﹣∠B＝90°．在Rt△ABC中，∵∠A＝30°，AB＝6cm．∴BC＝AB＝3cm．故答案为：3．13.【答案】：【解析】：∵是完全平方式，
∴，
解得．
故答案是：14.【答案】： 【解析】：等边三角形的每个内角的度数为，正方形的每个内角的度数为，正五边形的每个内角的度数为，如图，的外角和等于，，即，，又，，解得，故答案为：．15.【答案】： 或【解析】：解：∵AB=AC， ∴∠B=∠C=40°， ①当AD=AE时，∠ADE=∠AED=40°， ∵∠AED＞∠C， ∴此时不符合； ②当DA=DE时，即∠DAE=∠DEA=（180°-40°）=70°， ∵∠BAC=180°-40°-40°=100°， ∴∠BAD=100°-70°=30°； ∴∠BDA=180°-30°-40°=110°； ③当EA=ED时，∠ADE=∠DAE=40°， ∴∠BAD=100°-40°=60°， ∴∠BDA=180°-60°-40°=80°； ∴当△ADE是等腰三角形时，∠BDA的度数是110°或80°， 故答案为：110°或80°．三.解答题16【答案】：（1）；（2）一，见解析【解析】：（1）；（2）一，m（1＋m）−（m−1）2＝m＋m2−（m2−2m＋1）＝m＋m2−m2＋2m−1＝3m−1．17【答案】：, 0【解析】：= =-当x=1时，原式=-．18【答案】：（1）如图，△A'B'C'即所求作．见解析；（2）如图，点P即为所求作，见解析．【解析】：（1）如图，△A'B'C'即为所求作．（2）如图，点P即为所求作．19【答案】：（1）①作图见解析；②作图见解析；③作图见解析    （2）【解析】：【小问1详解】①解：如图1，射线AD就是∠BAC的角平分线； ②解：作∠EBC=∠ADC，点E就是所求作的点，如图1所示；③解：作线段的垂直平分线，如图1所示；【小问2详解】解：．由（1）可知∵∠CBE＝∠ADC∴∴，∴∴∴是等腰三角形∵∴．【点睛】本题考查了作角平分线、作一个角等于已知角、作线段的垂直平分线、等腰三角形的判定与性质．解题的关键在于对知识的灵活运用．20【答案】：（1）12；（2）①；②17【解析】：（1）∵，∴，∴；   （2）①∵，∴=，∴；    故答案为：；②设a=4-x，b=5-x，∵a-b=4-x-（5-x）=-1，∴，∴，∵ab=，∴，∴，故答案为：17．21【答案】：刘峰骑自行车每小时行20千米，李明乘公交车每小时行60千米【解析】：解：设刘峰骑自行车每小时行x千米，则李明乘公交车每小时行千米，根据题意，得，解得，经检验，是所列分式方程的解，且符合题意，∴（千米/时），答：刘峰骑自行车每小时行20千米，李明乘公交车每小时行60千米．22【答案】：（1）BD，证明见解析；（2）见解析；（3）见解析．【解析】：（1）延长AB至F，使BF＝BD，连接DF，根据三角形的外角性质得到∠ABC＝2∠F，则可利用SAS证明△ADF≌△ADC，根据全等三角形的性质可证明结论；（2）在AC上截取AE，使AE＝AB，连接DE，则可利用SAS证明△ADB≌△ADE，根据全等三角形的性质即可证明结论；（3）延长AB至G，使BG＝BD，连接DG，则可利用SSS证明△ADG≌△ADC，根据全等三角形的性质、角平分线的定义即可证明结论．【详解】证明：（1）如图1，延长AB至F，使BF＝BD，连接DF，则∠BDF＝∠F，∴∠ABC＝∠BDF＋∠F＝2∠F，∵AD平分∠BAC∴∠BAD＝∠CAD，∵AB＋BD＝AC，BF＝BD，∴AF＝AC，在△ADF和△ADC中，，∴△ADF≌△ADC（SAS），∴∠ACB＝∠F ，∴∠ABC＝2∠ACB．故答案为：BD．（2）如图3，在AC上截取AE，使AE＝AB，连接DE，∵AD，BD，CD分别平分∠BAC，∠ABC，∠ACB，∴∠DAB＝∠DAE，∠DBA＝∠DBC，∠DCA＝∠DCB，∵AB＋BD＝AC，AE＝AB，∴DB＝CE，△ADB和△ADE中，，∴△ADB≌△ADE（SAS），∴BD＝DE，∠ABD＝∠AED，∴DE＝CE，∴∠EDC＝∠ECD，∴∠AED＝2∠ECD， ∴∠ABD＝2∠ECD，∴∠ABC＝2∠ACB．（3）如图4，延长AB至G，使BG＝BD，连接DG，则∠BDG＝∠AGD，∴∠ABC＝∠BDG＋∠AGD＝2∠AGD，∵∠ABC＝2∠ACB，∴∠AGD＝∠ACB，∵AB＋BD＝AC，BG＝BD，∴AG＝AC，∴∠AGC＝∠ACG，∴∠DGC＝∠DCG，∴DG＝DC，在△ADG和△ADC中，，∴△ADG≌△ADC（SSS），∴∠DAG＝∠DAC，即AD平分∠BAC．【点睛】本题考查的是三角形全等的判定和性质、角平分线的定义，掌握全等三角形的判定定理和性质定理是解题的关键．