中考数学一轮考点复习统计与概率《数据分析》精练(2份打包，教师版+原卷版)

这是一份中考数学一轮考点复习统计与概率《数据分析》精练(2份打包，教师版+原卷版)，文件包含中考数学一轮考点复习统计与概率《数据分析》精练教师版doc、中考数学一轮考点复习统计与概率《数据分析》精练原卷版doc等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
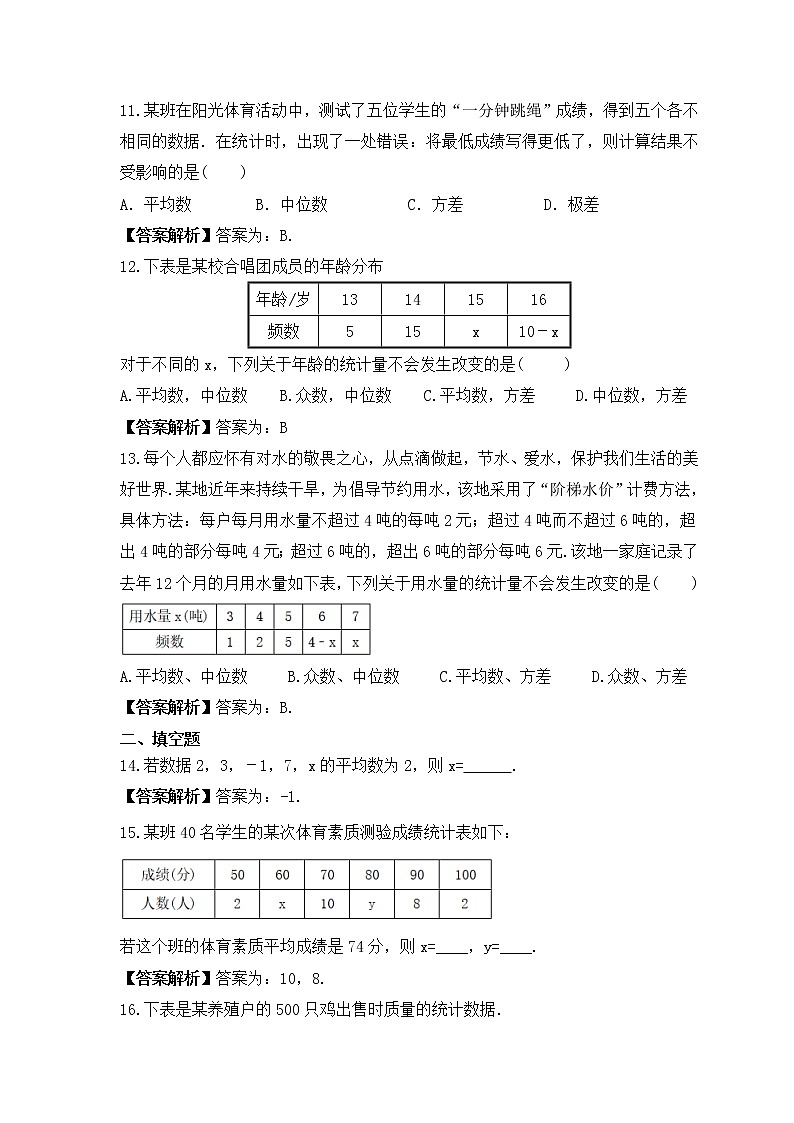
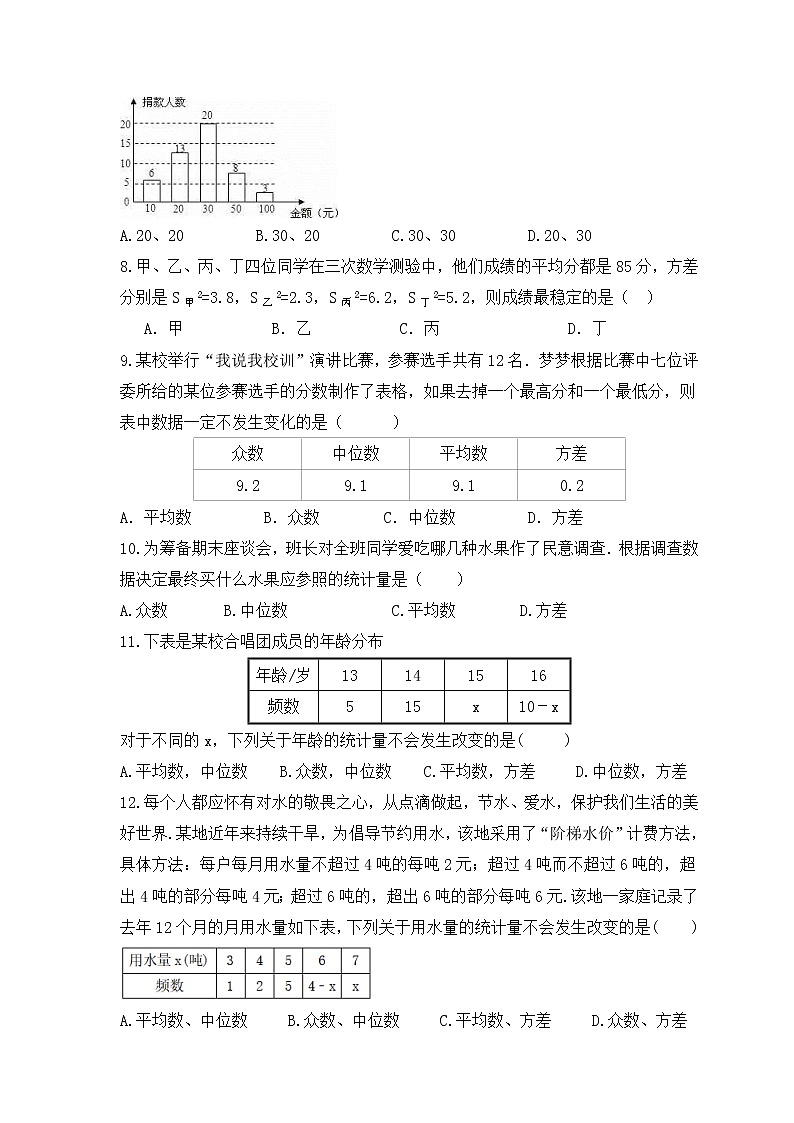
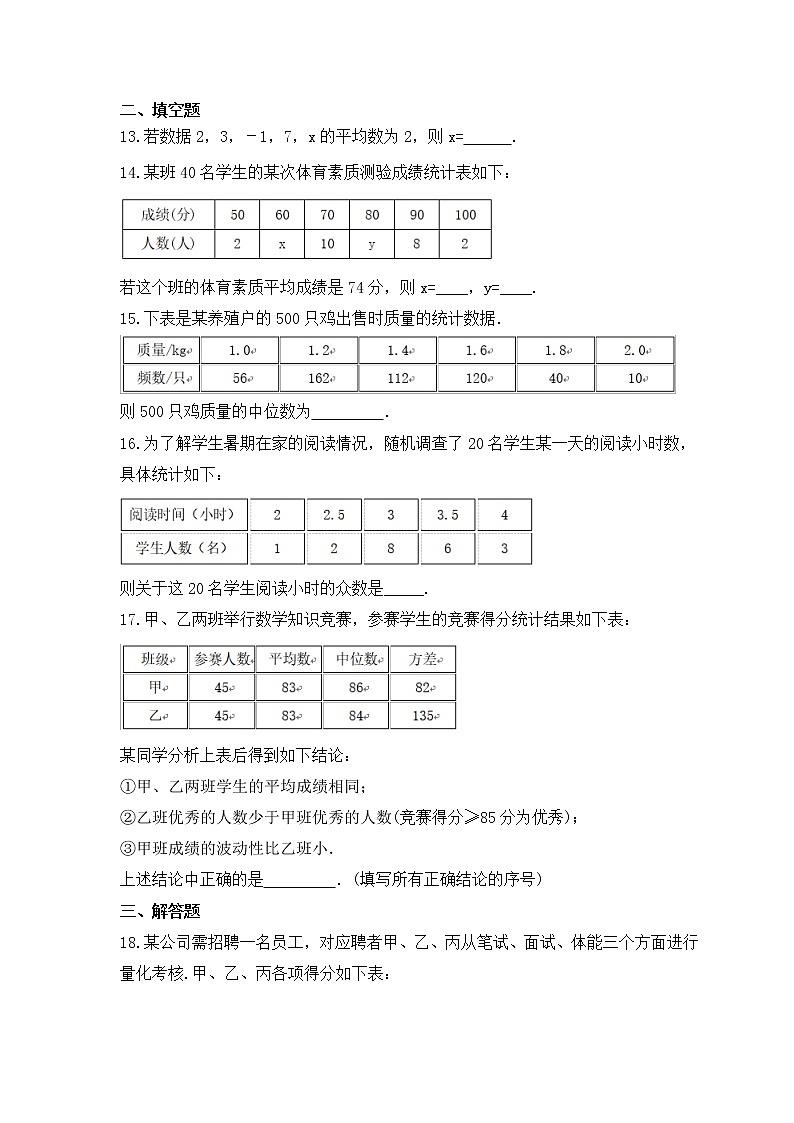
中考数学一轮考点复习统计与概率《数据分析》精练一              、选择题1.某次射击训练中，一个小组的成绩如下表所示：已知该小组的平均成绩为8.1环，那么成绩为8环的人数是(　　)A.4                 B.5                  C.6                       D.7【答案解析】B2.某校生物小组11人到校外采集标本，其中2人每人采集到6件，4人每人采集到3件，5人每人采集到4件，则这个小组平均每人采集标本(      ) A.3件     B.4件     C.5件     D.6件【答案解析】答案为：B3.已知x1，x2，x3，……，x10的平均数是5，x11，x12，x13，……，x20的平均数是3，则x1，x2，x3，……，x20的平均数是(  )A.5       B.4        C.3       D.8【答案解析】答案为：B4.某校九年级“诗歌大会”比赛中，各班代表队得分如下(单位：分)：9，7，8，7，9，7，6，则各代表队得分的中位数是(　　)A.9分         B.8分         C.7分         D.6分【答案解析】C5.中国奥运冠军朱启南在亚运会男子10米气步枪决赛中，凭借最后3枪的出色发挥，以总成绩702.2环夺得冠军。他在决赛中打出的10枪成绩(单位：环)是：10.4，9.6，10.4，10.1，10.2，10.7，10.2，10.5，10.7，10.4.则这组数据的中位数是(  )A.10.7   B.10.4   C.10.3    D.10.2【答案解析】答案为：B6.据统计，某校某班30名同学3月份最后一周每天按时做数学“小测题”的学生数依次是：27，30，29，25，26，28，29，那么这组数据的中位数和众数分别是（    ）A.25和30   B.25和29      C.28和30      D.28和29【答案解析】答案为：D.7.世界因爱而美好，在今年我校的“献爱心”捐款活动中，九年级三班50名学生积极加献爱心捐款活动，班长将捐款情况进行了统计，并绘制成了统计图，根据图中提供的信息，捐款金额的众数和中位数分别是（  ）A.20、20     B.30、20     C.30、30     D.20、30【答案解析】C8.甲、乙、丙、丁四位同学在三次数学测验中，他们成绩的平均分都是85分，方差分别是S甲2=3.8，S乙2=2.3，S丙2=6.2，S丁2=5.2，则成绩最稳定的是（  ）   A．甲                         B．乙                         C．丙                              D．丁【答案解析】9.某校举行“我说我校训”演讲比赛，参赛选手共有12名．梦梦根据比赛中七位评委所给的某位参赛选手的分数制作了表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（      ）众数中位数平均数方差9.29.19.10.2A．平均数                       B．众数                      C．中位数                       D．方差【答案解析】C10.为筹备期末座谈会，班长对全班同学爱吃哪几种水果作了民意调查．根据调查数据决定最终买什么水果应参照的统计量是（　　）                                          A.众数                     B.中位数                           C.平均数                      D.方差【答案解析】A．11.某班在阳光体育活动中，测试了五位学生的“一分钟跳绳”成绩，得到五个各不相同的数据．在统计时，出现了一处错误：将最低成绩写得更低了，则计算结果不受影响的是(　　)A．平均数     B．中位数      C．方差       D．极差【答案解析】答案为：B.12.下表是某校合唱团成员的年龄分布年龄/岁13141516频数515x10－x对于不同的x，下列关于年龄的统计量不会发生改变的是(     )A.平均数，中位数    B.众数，中位数    C.平均数，方差     D.中位数，方差【答案解析】答案为：B13.每个人都应怀有对水的敬畏之心，从点滴做起，节水、爱水，保护我们生活的美好世界.某地近年来持续干旱，为倡导节约用水，该地采用了“阶梯水价”计费方法，具体方法：每户每月用水量不超过4吨的每吨2元；超过4吨而不超过6吨的，超出4吨的部分每吨4元；超过6吨的，超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表，下列关于用水量的统计量不会发生改变的是(　　)A.平均数、中位数     B.众数、中位数     C.平均数、方差     D.众数、方差【答案解析】答案为：B.二              、填空题14.若数据2，3，－1，7，x的平均数为2，则x=      .【答案解析】答案为：-1.15.某班40名学生的某次体育素质测验成绩统计表如下：若这个班的体育素质平均成绩是74分，则x=____，y=____.【答案解析】答案为：10，8.16.下表是某养殖户的500只鸡出售时质量的统计数据．则500只鸡质量的中位数为　   　．【答案解析】答案为：1.4kg．17.为了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体统计如下：则关于这20名学生阅读小时的众数是_____.【答案解析】答案为：3.18.甲、乙两班举行数学知识竞赛，参赛学生的竞赛得分统计结果如下表：某同学分析上表后得到如下结论：①甲、乙两班学生的平均成绩相同；②乙班优秀的人数少于甲班优秀的人数(竞赛得分≥85分为优秀)；③甲班成绩的波动性比乙班小．上述结论中正确的是　   　．(填写所有正确结论的序号)【答案解析】答案为：①②③．三              、解答题19.某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表：(1)根据三项得分的平均分，从高到底确定三名应聘者的排名顺序； (2)该公司规定：笔试、面试、体能得分分别不得低于80分、80分、70分，并按60%，30%，10%的比例计入总分.根据规定，请你说明谁将被录用. 【答案解析】解：(1)x甲=84，x乙=80，x丙=81，∴x甲＞x丙＞x乙，∴排名顺序为甲、丙、乙(2)由题意可知，甲不符合规定不能被录用，又∵x乙′=85×60%＋80×30%＋75×10%=82.5，x丙′=80×60%＋90×30%＋73×10%=82.3，∴乙将被录用20.参与我市教育资源倍增工程的学校有A、B两个校区，为了加强融合，两个校区的学生特举办了以“弘扬校园真善美，文名礼仪在我心”为主题的演讲比赛．两校区参赛人数相等，比赛结束后，按分数进行分类统计，共有7分、8分、9分、10分（满分10分）四个等级．依据统计数据绘制了如下尚不完整的统计图表． （1）根据图表信息可知两个校区参加的人数为    人，并将图2的统计图补充完整；（2）经计算，B校区的平均分是8.3分，中位数是8分，请计算A校区的平均分、中位数，并从平均数和中位数的角度分析哪个校区成绩较好；（3）如果该学校要组织8人的代表队参加学区内的演讲团体赛，决定从这两个校区中的一所挑选参赛选手，请你分析，应选哪个小区？【答案解析】解：（1）20；补充统计图如图所示；  （2）A校区的平均分为8．     第10名与第11名都得7分，所以中位数为7分；     由于两校区平均分相等，B校区成绩的中位数大于A校区的中位数，     所以B校区的成绩较好．（3）因为选8名学生参加学区内的演讲团体赛，21.某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：（1）本次接受随机抽样调查的学生人数为   ，图①中m的值是   ；（2）求本次调查获取的样本数据的平均数、众数和中位数；（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．【答案解析】解：（1）根据条形图4+16+12+10+8=50（人），m=100﹣20﹣24﹣16﹣8=32；（2）∵=（5×4+10×16+15×12+20×10+30×8）/50=16，∴这组数据的平均数为：16，∵在这组样本数据中，10出现次数最多为16次，∴这组数据的众数为：10，∵将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是15，∴这组数据的中位数为：0.5（15+15）=15；（3）∵在50名学生中，捐款金额为10元的学生人数比例为32%，∴由样本数据，估计该校1900名学生中捐款金额为10元的学生人数比例为32%，有1900×32%=608，∴该校本次活动捐款金额为10元的学生约有608名．故答案为：50，32．22. “知识改变命运，科技繁荣祖国．”为提升中小学生的科技素养，我区每年都要举办中小学科技节．为迎接比赛，某校进行了宣传动员并公布了相关项目如下：A﹣﹣杆身橡筋动力模型；B﹣﹣直升橡筋动力模型；C﹣﹣空轿橡筋动力模型．右图为该校报名参加科技比赛的学生人数统计图．(1)该校报名参加B项目学生人数是_______人；(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是_______°；(3)为确定参加区科技节的学生人选，该校在集训后进行了校内选拔赛，最后一轮复赛，决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛，每人进行了4次试飞，对照一定的标准，判分如下：甲：80，70，100，50；乙：75，80，75，70．如果你是教练，你打算安排谁代表学校参赛？请说明理由．【答案解析】解：(1)∵参加科技比赛的总人数是6÷25%=24，∴报名参加B项目学生人数是24×41.67%=10，故答案为10；(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是：360°×(1﹣25%﹣41.67%)=120°，(3)∵甲的平均数=乙的平均数=75，∴S2甲=[(80﹣75)2+(70﹣75)2+(100﹣75)2+(50﹣75)2]=325，S2乙=[(75﹣75)2+(80﹣75)2+(75﹣75)2+(70﹣75)2]=12.5，∵S2甲＞S2乙，∴选乙．23.某校为了了解初中学生每天的睡眠时间(单位为小时)，随机调查了该校的部分初中学生，根据调查结果，绘制出如下统计图．请根据相关信息，解答下列问题：(1)本次接受调查的初中学生人数为___________人，扇形统计图中的m=________，条形统计图中的n=_____；(2)所调查的初中学生每天睡眠时间的众数是____________，方差是___________；(3)该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数．【答案解析】解：(1)由图表中的数据可得：8÷20%=40人，10÷40×100%=25%，即m=25，40×37.5%=15人，即n=15，故答案为：40；25；15；(2)由条形统计图可得：∵睡眠时间诶7h的人数为15人，最多，∴众数是：7，平均数是：7，方差是1.15，(3)1080人，∴该校初中学生每天睡眠时间不足8小时的人数为1080人．24.某校举办了一次成语知识竞赛，满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀，这次竞赛中，甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下所示．(1)求出下列成绩统计分析表中a，b的值：组别平均分中位数方差合格率优秀率甲组6.8a3.7690%30%乙组b7.51.9680%20%(2)小英同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上面表格判断，小英是甲、乙哪个组的学生；(3)甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你写出两条支持乙组同学观点的理由．【答案解析】解：(1)由折线统计图可知，甲组成绩从小到大排列为：3，6，6，6，6，6，7，9，9，10，∴a=6，b=7.2.(2)∵甲组的中位数为6，乙组的中位数为7.5，而小英的成绩位于小组中上游，∴小英属于甲组学生．(3)①乙组的平均分高于甲组，即乙组的总体平均水平高；②乙组的方差比甲组小，即乙组的成绩比甲组的成绩稳定．25.在6.26国际禁毒日到来之际，贵阳市教育局为了普及禁毒知识，提高禁毒意识，举办了“关爱生命，拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人，现从中各随机抽取20名同学的测试成绩进行调查分析，成绩如下：(1)根据上述数据，将下列表格补充完成.整理、描述数据：分析数据：样本数据的平均数、中位数、满分率如表：得出结论：(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共　   　人；(3)你认为哪个年级掌握禁毒知识的总体水平较好，说明理由.【答案解析】解：(1)由题意知初二年级的分数从小到大排列为69、69、79、79、89、94、95、96、97、97、98、98、99、99、99、99、100、100、100、100，所以初二年级成绩的中位数为97.5分，补全表格如下：年级平均数中位数满分率初一90.19325%初二92.897.520%(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共300×25%+300×20%=135人，故答案为：135；(3)初二年级掌握禁毒知识的总体水平较好，∵初二年级的平均成绩比初一高，说明初二年级平均水平高，且初二年级成绩的中位数比初一大，说明初二年级的得高分人数多于初一，∴初二年级掌握禁毒知识的总体水平较好.