2022西宁高三高考二模数学（理）试题含解析

这是一份2022西宁高三高考二模数学（理）试题含解析，文件包含青海省西宁市2021-2022学年高三高考二模数学理试题含解析docx、青海省西宁市2021-2022学年高三高考二模数学理试题无答案docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
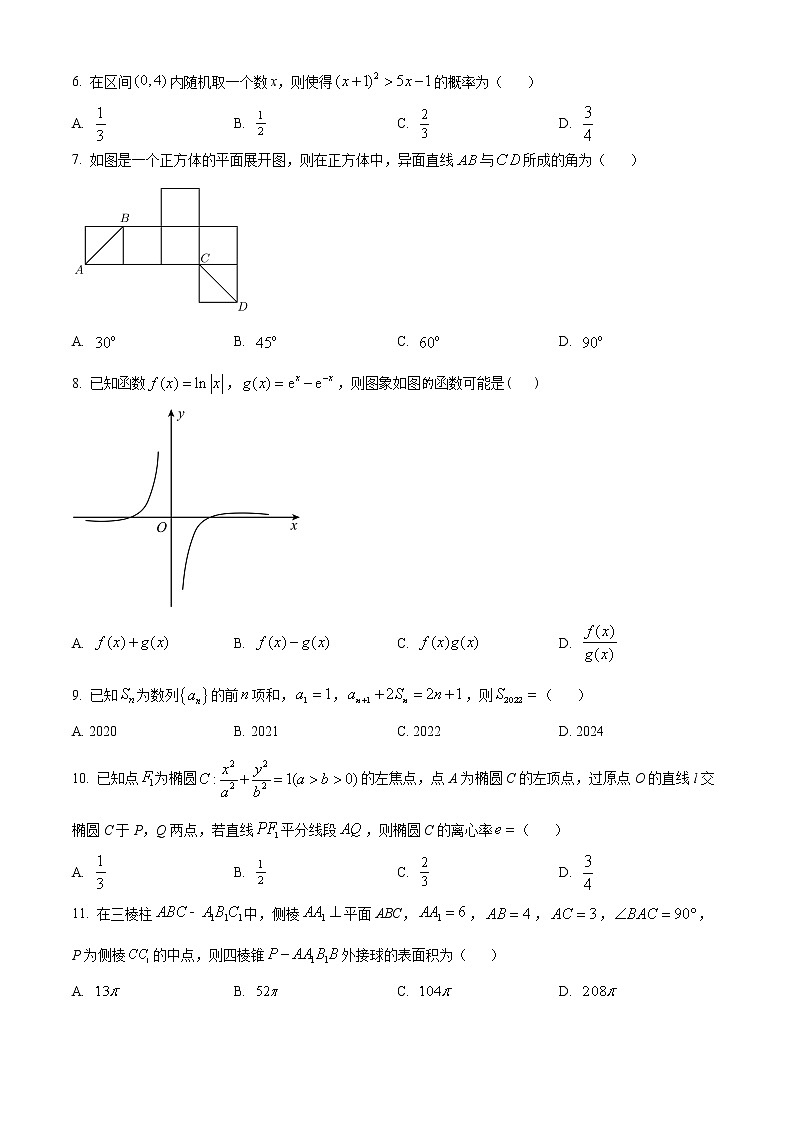
2022年普通高等学校招生全国统一考试西宁市高三年级复习检测（二）理科数学试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 集合，，则图中阴影部分表示的集合为A.  B.  C.  D. 【答案】B【解析】【详解】图中阴影部分表示为，因为，所以，故选.2. 设为虚数单位，则复数（    ）A.  B.  C.  D. 【答案】A【解析】【分析】利用复数除法运算求得正确答案.【详解】.故选：A3. 已知在平行四边形ABCD中，，，对角线AC与BD相交于点M，（    ）A.  B.  C.  D. 【答案】D【解析】【分析】根据向量加法的几何意义可得，应用向量线性运算的坐标表示，即可求的坐标.【详解】由题设，.故选：D.4. 在北京冬奥会开幕式上，二十四节气倒计时惊艳了世界．从冬至之日起，小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影长依次成等差数列，若冬至的日影长为18.5尺，立春的日影长为15.5尺，则立夏的日影长为（    ）A. 9.5 尺 B. 10.5 尺 C. 11.5 尺 D. 12.5 尺【答案】A【解析】【分析】由等差数列相关运算得到公差，进而求出立夏的日影长.【详解】由题意得：为等差数列，公差为d，则，，则，解得：，则，故立夏的日影长为9.5尺.故选：A5. 的展开式中，的系数为（    ）A. 40 B.  C. 80 D. 【答案】D【解析】【分析】求出的展开式为，在令，即可求出结果.【详解】因为的展开式为令，所以的系数为.故选：D.6. 在区间内随机取一个数x，则使得的概率为（    ）A.  B.  C.  D. 【答案】D【解析】【分析】求出不等式在上的解集，利用几何概型概率公式可求得所求事件的概率.【详解】由，有，解得或，又，故所求概率为.故选：D.7. 如图是一个正方体的平面展开图，则在正方体中，异面直线与所成的角为（    ）A.  B.  C.  D. 【答案】C【解析】【分析】把展开图还原成正方体，由于且相等，故异面直线与所成的角就是和所成的角，由于是等边三角形可得答案.【详解】把展开图还原成正方体如图所示，由于且相等，故异面直线与所成的角就是和所成的角，故 (或其补角)为所求，再由是等边三角形，可得.故选：C.8. 已知函数，，则图象如图的函数可能是(    )A.  B.  C.  D. 【答案】D【解析】【分析】结合函数图像的奇偶性和单调性即可判断.【详解】由图可知，该函数奇函数，和为非奇非偶函数，故A、B不符；当x＞0时，单调递增，与图像不符，故C不符；为奇函数，当x→＋时，∵y＝的增长速度快于y＝lnx的增长速度，故＞0且单调递减，故图像应该在x轴上方且无限靠近x轴，与图像相符.故选：D.9. 已知为数列的前项和，，，则（    ）A. 2020 B. 2021 C. 2022 D. 2024【答案】C【解析】【分析】利用化简可得出，则可求出答案.【详解】当时， ，当时，由得，两式相减可得，即，所以，可得，所以.故选：C.10. 已知点为椭圆的左焦点，点A为椭圆C的左顶点，过原点O的直线l交椭圆C于P，Q两点，若直线平分线段，则椭圆C的离心率（    ）A.  B.  C.  D. 【答案】A【解析】【分析】直接由条件判断出为的重心，利用重心的性质即可求解.【详解】∵为线段的中线，为线段的中线，∴为的重心，∴，即．故选：A.11. 在三棱柱中，侧棱平面ABC，，，，，P为侧棱的中点，则四棱锥外接球的表面积为（    ）A.  B.  C.  D. 【答案】B【解析】【分析】连接，交于点O，连接OP．根据题意数量关系求得，得到，又在矩形中，，得到点为四棱锥外接球的球心，可得外接球的半径，进而得到表面积.【详解】连接，交于点O，连接OP．因为平面ABC，所以在矩形中，由P为的中点，知．在中，，所以．在中，，所以，所以，又O为的中点，所以，又在矩形中，，所以点为四棱锥外接球的球心，所以外接球的半径，其表面积，故选：B．12. 定义方程的实根叫做函数的“新驻点”，若函数，，的“新驻点”分别为，，，则，，的大小关系为（    ）A.  B.  C.  D. 【答案】B【解析】【分析】分别求出导函数，由导函数与原函数相等列出方程，直接解得，再引入新函数，利用新函数的导数确定新函数的零点所在区间，得的范围从而确定它们的大小．【详解】由题意：，所以分别为的根，即为函数的零点，可解得；为单调递增函数，且，所以，令，解得，或，当时，，单调递增，当时，，单调递减，当时，，单调递增，由，，，，所以，所以.故选：B.二、填空题：本题共4小题，每小题5分，共20分．13. 在数列中，，且，则________．【答案】【解析】【分析】由题知，，然后两式相除，可得答案.【详解】由题知  ①∴有  ②由①÷②，可得，∴.故答案为：.14. 已知双曲线的左､右焦点分别为，，点P是双曲线左支上一点且，则______．【答案】3【解析】【分析】根据双曲线方程求出，再根据双曲线的定义可知，即可得到、，再由正弦定理计算可得；【详解】解：因为双曲线为，所以、，因为点P是双曲线左支上一点且，所以，所以，，在中，由正弦定理可得，所以；故答案：15. 将某射击运动员的十次射击成绩（环数）按从小到大的顺序（相等数据相邻排列）排列为：8.1，8.4，8.4，8.7，x，y，9.3，9.4，9.8，9.9，已知总体的中位数为9，则的最小值为__________．【答案】【解析】【分析】由中位数的概念结合基本不等式可得.【详解】因为总体的中位数为9．所以，则，当且仅当时等号成立．故答案为：16. 已知定义在R上的可导函数的导函数为，满足，且为偶函数，，则不等式的解集为______．【答案】【解析】【分析】构造，利用导数研究单调性，由题设知对称轴为，即可得，进而求，而原不等式等价于，即可求解集.【详解】设，则，又，所以，即在R上是减函数，因为为偶函数，所以图象关于y轴对称，而向右平移3个单位可得，所以对称轴为，则，所以，不等式等价于，故，所以不等式的解集为.故答案为：三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17. 在①；②；③这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求的值；若问题中的三角形不存在，说明理由．问题：是否存在，它的内角A，，的对边分别为，，，面积为S，且，，________？【答案】答案不唯一，具体见解析【解析】【分析】根据题干条件及余弦定理、面积公式，可求得角C的值，若选①，根据正弦定理，可求得的值，根据大边对大角原则，可得角A只有一解，根据同角三角函数关系，可求得的值；若选②，根据正弦定理，可求得的值，根据大边对大角原则，可得角A有两解，根据同角三角函数关系，可求得的值；若选③，根据正弦定理，可求得的值，因为，则三角形无解.【详解】由题意可知在中，因为，且，所以，由余弦定理可知，所以因为，所以；          若选①，由正弦定理可得，解得，          在中，因为，所以，又因为，则角A只有一解，且，          所以． 若选②，由正弦定理可得，解得，          在中，因为，所以，又因为，则角A有两解，          所以．          若选③，由正弦定理可得，解得，          因为，所以无解，即三角形不存在．18. 某中学有初中学生1800人，高中学生1200人，为了解学生本学期课外阅读时间，现采用分成抽样的方法，从中抽取了100名学生，先统计了他们课外阅读时间，然后按“初中学生”和“高中学生”分为两组，再将每组学生的阅读时间（单位：小时）分为5组：[0，10），[10，20），[20，30），[30，40），[40，50]，并分别加以统计，得到如图所示的频率分布直方图.（1）写出a的值；（2）试估计该校所有学生中，阅读时间不小于30个小时的学生人数；（3）从阅读时间不足10个小时的样本学生中随机抽取3人，并用X表示其中初中生的人数，求X的分布列和数学期望.【答案】（1）a＝0.03；（2）870人；（3）分布列见解析，.【解析】【分析】（1）根据频率频率直方图的性质，可求得a的值；（2）由分层抽样，求得初中生有60名，高中有40名，分别求得初高中生阅读时间不小于30小时的学生的频率及人数，求和；（3）分别求得初高中生中阅读时间不足10个小时的学生人数，写出X的取值及概率，写出分布列和数学期望.【详解】解：（1）由频率直方图的性质，（0.005+0.02+a+0.04+0.005）×10＝1，解得a＝0.03，（2）由分层抽样可知：抽取初中生有60名，高中有40名，∵初中生中，阅读时间不小于30小时的学生的频率为（0.03+0.005）×10＝0.25，∴所有的初中生阅读时间不小于30小时的学生约有0.25×1800＝450人，同理，高中生阅读时间不小于30小时的学生的频率为（0.03+0.005）×10＝0.035，学生人数约为0.35×1200＝420人，所有的学生阅读时间不小于30小时的学生约有450+420＝870，（3）初中生中阅读时间不足10个小时的学生的频率为0.005×10＝0.05，样本人数为0.05×60＝3人，同理，高中生中阅读时间不足10个小时的学生的频率为0.005×10×40＝2，故X的可能取值为：1，2，3，P（X＝1）＝＝，P（X＝2）＝＝，P（X＝3）＝＝，∴X的分布列为： X 1 2 3 P  ∴E（X）＝1×+2×+3×＝.19. 如图，为圆锥的顶点，为底面圆心，点，在底面圆周上，且，点，分别为，的中点．求证：；若圆锥的底面半径为，高为，求直线与平面所成的角的正弦值．【答案】证明见解析；.【解析】【分析】利用线面垂直的判定定理和线面垂直的性质定理即可证明；建立空间直角坐标系，结合向量的数量积运算求出直线与平面所成的角的正弦值．【详解】解：由题意，得底面圆，点，分别为，的中点，， 底面圆，在底面圆上，．，为正三角形，又因为为的中点，，又因为，且平面，平面，平面，平面，．如图，以为原点，，，所在直线为轴，轴，轴建立空间直角坐标系，则，，，，故，，，设平面的法向量为，由，可得，令，得为平面的一个法向量，设直线与平面所成的角为，则，即直线与平面所成的角的正弦值为．【点睛】本题考查线线垂直的判定，以及线面所成角的正弦值的求法，考查分析问题能力，运算求解能力，属于中档题.20. 已知定点，定直线，动圆过点，且与直线相切.（1）求动圆的圆心轨迹的方程；（2）过焦点的直线与抛物线交于两点，与圆交于两点（，在轴同侧），求证：是定值.【答案】（1）    （2）1【解析】【分析】（1）利用抛物线的定义先判定动点的轨迹形状，再求其标准方程；（2）设出直线方程，联立直线和抛物线方程，得到关于的一元二次方程，利用根与系数的关系、抛物线的定义进行证明.【小问1详解】解：由题意，得动圆的圆心到点的距离等于到直线的距离，所以的轨迹是以点为焦点的抛物线，其轨迹方程为；【小问2详解】解：设经过焦点的直线为，联立，得；设，，则，且，；因为圆的圆心为（即抛物线的焦点），半径为，由抛物线的定义，得，，则，，所以，即是定值，定值是1.21 已知函数，.（1）讨论的单调性；（2）若关于的不等式在上恒成立，求的取值范围.【答案】（1）在上单调递增，在上单调递减    （2）【解析】【分析】（1）求出导函数，利用的范围，判断导函数的符号，推出函数的单调区间即可.（2）不等式等价于在上恒成立，构造函数，通过函数的导数，利用二次函数的性质，说明极值点一正一负，设函数，利用导函数，结合函数的单调性，转化求解的范围即可.【小问1详解】解：（1）因为的定义域为，且.①若，则，所以在上单调递增.②若，令，得.当时，；当时，.所以在上单调递增，在上单调递减.【小问2详解】（2）不等式在上恒成立等价于在上恒成立，令，则.对于函数，，所以其必有两个零点.又两个零点之积为-1，所以两个零点一正一负，设其中一个零点，则，即.此时在上单调递增，在上单调递减，故，即.设函数，则.当时，；当时，.所以在上单调递减，在上单调递增.又，所以.由在上单调递增，得.故的取值范围为.（二）选考题：共10分．请考生在第22、23题中任选一题做答．如果多做，则按所做的第一题记分． [选修4-4：坐标系与参数方程]22. 在直角坐标系xOy中，，曲线C的参数方程为(为参数)，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为(，)（1）求曲线C的极坐标方程；（2）已知曲线C与直线l交于A，B两点，若，求直线l的直角坐标方程.【答案】（1）；（2）.【解析】【分析】（1）首先将曲线C的参数方程华为普通方程，再将其转化为极坐标方程即可；（2）根据极坐标系中的几何意义,结合三角函数知识进行解题即可.【详解】解：（1）由曲线C的参数方程(为参数)，得曲线C的普通方程为，得，即曲线C的极坐标方程为.（2）将直线l的极坐标方程代入曲线C的极坐标方程，得，设，，，，又，，所以，即，因为，所以或，所以直线的直角坐标方程为.【点睛】求解与极坐标有关的问题的主要方法：（1）直接利用极坐标系求解，可与数形结合思想配合使用；（2）转化为直角坐标系，用直角坐标求解.使用后一种方法时，应注意若结果要求的是极坐标，还应将直角坐标化为极坐标. [选修4-5：不等式选讲]23. 已知函数.（1）当时，解不等式；（2）当时，，求实数a的取值范围.【答案】（1）    （2）【解析】【分析】（1）根据绝对值的定义分类讨论解不等式可得；（2）先化简不等式，然后按和分类讨论，由不等式的解得结论．【小问1详解】当a=2时，，当时，，解得，所以当时，，解得，所以；当时，，无解，综上所述，不等式的解集为【小问2详解】当时，等价于成立.当，且时，，不合题意；当时，的解集为，所以，故.综上所述，实数的取值范围为.