【暑假班】苏教版数学四升五衔接精编讲义 专题07《三角形、平行四边形和梯形》（解析版）

这是一份【暑假班】苏教版数学四升五衔接精编讲义 专题07《三角形、平行四边形和梯形》（解析版），共15页。试卷主要包含了定义，三角形的高，三角形三边的关系，三角形的内角和，三角形的分类等内容，欢迎下载使用。
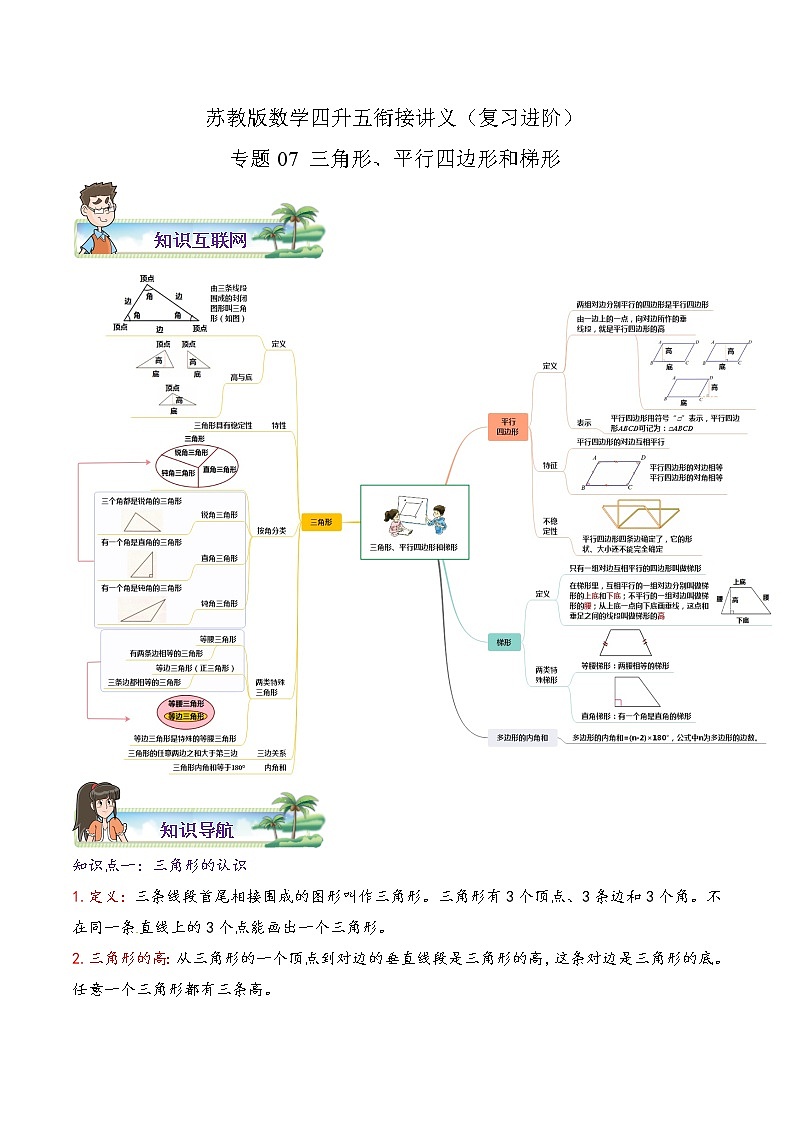
苏教版数学四升五衔接讲义（复习进阶）专题07 三角形、平行四边形和梯形知识点一：三角形的认识1.定义：三条线段首尾相接围成的图形叫作三角形。三角形有3个顶点、3条边和3个角。不在同一条直线上的3个点能画出一个三角形。2.三角形的高：从三角形的一个顶点到对边的垂直线段是三角形的高，这条对边是三角形的底。任意一个三角形都有三条高。3.三角形三边的关系：三角形任意两边长度的和大于第三边。4.三角形的内角和：三角形的内角和等于180°5.三角形具有稳定性（也就是当一个三角形的三条边的长度确定后，这个三角形的形状和大小都不会改变），生活中很多物体利用了这样的特性。如：人字梁、斜拉桥、自行车车架。6.三角形的分类：三个角都是锐角的三角形是锐角三角形有一个角是直角的三角形是直角三角形有一个角是钝角的三角形是钝角三角形。任意一个三角形至少有两个锐角。7.等腰三角形和等边三角形和等腰直角三角形：两条边相等的三角形是等腰三角形，相等的两条边叫做腰，另外一条边叫做底，两条腰的夹角叫做顶角，底和腰的夹角叫做底角，两个底角相等，等腰三角形是轴对称图形，有一条对称轴。三条边都相等的三角形是等边三角形，三条边都相等，三个角也  都相等（每个角都是 60°，所有等边三角形的三个角都是60°。）等边三角形是轴对称图形，有三条对称轴。有一个角是直角的等腰三角形叫做等腰直角三角形，它的底角等于45°，顶角等于90°等腰三角形的顶角=180°－底角×2     等腰三角形的底角=（180°－顶角）÷2一个三角形最大的角是 60 度，这个三角形一定是等边三角形。多边形的内角和=180°×（边数－2）知识点二：平行四边形的认识1.定义：两组对边分别平行的四边形叫平行四边形，它的对边平行且相等，对角相等。从一个顶点向对边可以作两种不同的高。一个平行四边形有无数条高。2.特征：平行四边形有4条边，4个角；平行四边形的两组对边分别平行且想等；平行四边形的两组对角分别相等。3.平行四边形容易变形（不稳定性）：生活中许多物体都利用了这样的特性。如：电动伸缩门、铁拉门、伸降机。把平行四边形拉成一个长方形，周长不变，面积变了。平行四边形不是轴对称图形。4.用两块(完全一样)的三角尺可以拼成一个平行四边形，正方形、长方形属于特殊的平行四边形。知识点三：梯形的认识1.定义：只有一组对边平行的四边形叫梯形。平行的一组对边分别是梯形的上底和下底，不平行的一组对边叫做梯形的腰，从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高（无数条）。2.梯形的分类及特征：两条腰相等的梯形叫等腰梯形，它的两个底角相等，等腰梯形是轴对称图形，有一条对称轴；有一个角是直角的梯形叫直角梯形，直角梯形有两组邻边互相垂直3.两个（完全一样）的梯形可以拼成一个平行四边形。一．选择题（共5小题，满分10分，每小题2分）1．（2分）（2022春•乳源县期中）一个三角形的两个内角分别是34°和48°，它是一个（　　）三角形。A．锐角 B．直角 C．钝角【思路引导】因为三角形的内角度数和是180°，已知两个角的度数，用180°减去这两个角的度数和即可求出第三个角，再看最大的角是什么角，这个三角形就是什么三角形。【完整解答】解：180°﹣（34°+48°）＝180°﹣82°＝98°这个三角形中最大的角是98°，是一个钝角，所以这个三角形是钝角三角形。故选：C。【考察注意点】解决本题关键是明确三角形的内角和是180度，以及三角形按角分类的方法。2．（2分）（2022春•交城县期中）七巧板是一种古老的中国传统智力玩，其中1号和2号两个三角形拼成的大三角形的内角和是（　　）°。A．180 B．360 C．以上答案都不对【思路引导】根据三角形的内角和等于180°，解答此题即可。【完整解答】解：1号和2号两个三角形拼成的大三角形的内角和是180°。故选：A。【考察注意点】熟练掌握三角形的内角和知识，是解答此题的关键。3．（2分）（2022春•乳源县期中）把一个平行四边形框架拉成一个长方形框架，它的周长（　　）A．变大 B．变小 C．不变【思路引导】把一个平行四边形框架拉成一个长方形框架，四条边的长度不会发生改变，因此它的周长不变。据此即可判断。【完整解答】解：把一个平行四边形框架拉成一个长方形框架，它的周长不变。故选：C。【考察注意点】解答此题的关键是明确四边形的形状虽然发生了变化，但每条边长都没有发生变化，周长就不发生变化。4．（2分）（2022春•高台县期中）如图，学校伸缩门里有许多小平行四边形，这是应用了平行四边形（　　）的性质。A．容易变形 B．对边相等 C．稳定性【思路引导】根据平行四边形的不稳定性，解答此题即可。【完整解答】解：学校伸缩门里有许多小平行四边形，这是应用了平行四边形的容易变形性质。故选：A。【考察注意点】熟悉平行四边形的不稳定性，是解答此题的关键。5．（2分）（2021春•厦门期末）下列方法中，不能验证“一个四边形的内角和是360°”的是（　　）A．分别量四个内角的度数，再相加 B．把四个角撕下来，拼成一个周角 C．把四个角折成一个平角 D．把四边形分成两个三角形，再用180°×2＝360°【思路引导】要想求出四边形的内角和，可以用量角器分别量出四个内角的度数，再相加；也可以把四个角撕下来，拼成一个周角；还可以把四边形分成两个三角形，根据三角形的内角和是180度，求出四边形的内角和。据此解答。【完整解答】解：由分析得：A、分别量出四个内角的度数，再相加。此方法正确。B、把四个角撕下来，拼成一个周角。此方法正确。C、把四个角折成一个平角。此方法错误。D、还可以把四边形分成两个三角形，再用180°×2＝360°。此方法正确。故选：C。【考察注意点】此题考查的目的是理解掌握求四边形内角和的方法及应用。二．填空题（共9小题，满分19分）6．（2分）（2022春•交城县期中）有1.5cm、2cm、3.5cm和5cm的4根小棒，取其中三根能围成一个三角形，这个三角形的周长是 　10.5　cm。【思路引导】任意三角形的两边之和必须大于第三边，任意两边的差必须小于第三边，据此选出3条线段，把三条线段相加即可求出三角形的周长，据此解答。【完整解答】解：因为2+3.5＞5，所以2厘米、3.5厘米和5厘米可以围成一个三角形。周长：2+3.5+5＝10.5（厘米）。故答案为：10.5。【考察注意点】本题考查了三角形的三边关系的应用。7．（2分）（2022春•项城市期中）从如图所示的4根小木棒中选3根围三角形，可以选 　①、③、④　，也可以选 　②、③、④　。【思路引导】根据三角形任意两边之和大于第三边，解答此题即可。【完整解答】解：6+13＞157+13＞15答：从如图所示的4根小木棒中选3根围三角形，可以选①、③、④，也可以选②、③、④。故答案为：①、③、④；②、③、④。【考察注意点】熟练掌握三角形的三边关系，是解答此题的关键。8．（3分）（2022春•项城市期中）∠1，∠2，∠3是一个三角形的3个内角，已知∠1＝∠2＝60°，那么∠3＝　60　°，这是一个 　等边　三角形，也是一个 　锐角　三角形。【思路引导】根据三角形的内角和等于180°和三角形的分类，解答此题即可。【完整解答】解：180﹣60﹣60＝60（度）答：∠3＝60°，这是一个等边三角形，也是一个锐角三角形。故答案为：60；等边；锐角。【考察注意点】熟练掌握三角形的内角和知识和三角形的分类，是解答此题的关键。9．（2分）（2022春•乳源县期中）在一个三角形中，至少有 　2　个锐角。【思路引导】我们知道锐角三角形有3个锐角，直角三角形有2个锐角，钝角三角形也有2个锐角，所以在一个三角形中，至少有2个锐角。【完整解答】解：在一个三角形中，至少有2个锐角。故答案为：2。【考察注意点】本题考查了对三角形特征的掌握情况。10．（2分）（2022春•乐陵市期中）有两根小棒，长度分别为17厘米、11厘米，再拿一根小棒就可以拼成三角形。第三根小棒最长 　27　厘米，最短 　7　厘米。（取整厘米数）【思路引导】根据三角形任意两边之和大于第三边，两边之差小于第三边，解答此题即可。【完整解答】解：17﹣11＝6（厘米）17+11＝28（厘米）6厘米＜第三边＜28厘米答：第三根小棒最长27厘米，最短7厘米。故答案为：27；7。【考察注意点】熟练掌握三角形的三边关系，是解答此题的关键。11．（2分）（2022春•德州期中）等腰三角形的一个底角是35°，那么它的顶角是 　110　°，如果它的顶角是102°，那么它的一个底角是 　39　°。【思路引导】根据三角形的内角和等于180°和等腰三角形的两腰相等，解答此题即可。【完整解答】解：180﹣35﹣35＝110（度）（180﹣102）÷2＝78÷2＝39（度）答：等腰三角形的一个底角是35°，那么它的顶角是110°，如果它的顶角是102°，那么它的一个底角是39°。故答案为：110；39。【考察注意点】熟练掌握等腰三角形的性质和三角形的内角和，是解答此题的关键。12．（2分）（2015春•夏邑县校级期末）一个长方形的桌子，锯掉一个角后，还剩下　3或4或5　只角，这些角的度数之和是　180或360或540　度．【思路引导】长方形的桌子据掉一个角以后可能是：三角形或四边形或五边形，根据多边形的内角和定理即可解决．【完整解答】解：长方形的桌子据掉一个角以后可能是：三角形或四边形或五边形，即还剩下3或4或5只角，180°×（3﹣2）＝180°180°×（4﹣2）＝360°180°×（5﹣2）＝540°因而这些角的度数之和是180或360或540度．故答案为：180或360或540．【考察注意点】本题考查了多边形的内角和，正确理解一个长方形据掉一个角以后得到的多边形的形状是解决本题的关键．13．（2分）一个多边形的每一个外角都等于30°，这个多边形的边数是　12　，它的内角和是　1800度　．【思路引导】任何一个多边形的外角都等于360°，用360除以每一个外角的度数就是这个多边形的边数，再根据多边形的内角和公式：（n﹣2）×180，即可求出它的内角和．【完整解答】解：360÷30＝12（条）（12﹣2）×180＝10×180＝1800（度）答：这个多边形的边数是12，它的内角和是1800度．故答案为：12，1800度．【考察注意点】本题考查了多边形的外角和与多边形的内角和公式的灵活应用．14．（2分）（2020春•衡水期末）一个三角形中，最大的角是78°．按角分，这个三角形是　锐角　三角形．【思路引导】小于90度的角叫做锐角，3个角都是锐角的三角形叫做锐角三角形．据此解答．【完整解答】解：一个三角形中，最大的角是78°．按角分，这个三角形是锐角三角形．故答案为：锐角．【考察注意点】此题考查的目的是理解掌握锐角的意义、三角形的内角和、三角形按照角的大小分类及应用．三．判断题（共5小题，满分10分，每小题2分）15．（2分）（2022春•德州期中）用一根3cm、一根2cm和一根5cm长的小棒可以围成一个三角形。 　×　（判断对错）【思路引导】根据三角形任意两边之和大于第三边，解答此题即可。【完整解答】解：2+3＝5所以用一根3cm、一根2cm和一根5cm长的小棒不可以围成一个三角形。所以题干说法是错误的。故答案为：×。【考察注意点】熟练掌握的三边关系，是解答此题的关键。16．（2分）（2022春•聊城期中）因为平行四边形具有不稳定性，所以把一个平行四边形拉成长方形，周长变了。 　×　（判断对错）【思路引导】把一个平行四边形拉成长方形，围成图形的四条边的长度没变，所以周长没变。【完整解答】解：把一个平行四边形拉成长方形，周长不变。故答案为：×。【考察注意点】根据平行四边形周长的含义，解答此题即可。17．（2分）（2022春•岷县月考）从长为3cm、5cm、7cm和9cm的四条线段中，任选三条组成三角形，可组成4种不同的三角形。 　×　（判断对错）【思路引导】三角形的任意两边之和必须大于第三边，任意选3个数字，把最小的两个数相加与较大的数作比较即可判断。【完整解答】解：3+5＞7，这一组可以组成三角形；3+7＞9，可以组成三角形；5+7＞9，可以组成三角形，3+5＜9，不可以组成三角形。因此只能有3组组成不同的三角形。原题说法错误。故答案为：×。【考察注意点】本题考查了三角形的三边关系的应用。18．（2分）（2022春•广平县期中）长分别为4厘米、5厘米、9厘米的三根小棒，可以围成一个三角形。 　×　（判断对错）【思路引导】根据三角形任意两边之和大于第三边，解答此题即可。【完整解答】解：因为4+5＝9所以长分别为4厘米、5厘米、9厘米的三根小棒，不可以围成一个三角形。所以题干说法是错误的。故答案为：×。【考察注意点】熟练掌握三角形的三边关系，是解答此题的关键。19．（2分）（2021秋•黄梅县期末）平行四边形的对边相等，对角也相等．　√　（判断对错）【思路引导】平行四边形的特征：对边平行且相等，对角相等；据此判断．【完整解答】解：由分析可知：平行四边形的对边相等，对角也相等．故答案为：√．【考察注意点】此题考查了长方形和正方形、平行四边形的特征，应注意理解和掌握．四．计算题（共1小题，满分6分，每小题6分）20．（6分）（2021春•古丈县期末）算出下面∠A和∠D的度数。【思路引导】根据三角形的内角和等于180°，四边形的内角和等于360°，解答此题即可。【完整解答】解：∠A＝180°﹣38°﹣（180°﹣80°）＝180°﹣38°﹣100°＝42°∠D＝360°﹣40°﹣90°﹣115°＝115°【考察注意点】熟练掌握三角形的内角和、四边形的内角和，是解答此题的关键。五．应用题（共5小题，满分26分）21．（5分）（2022春•项城市期中）杨奶奶家有一块三角形菜地，其中最大角是最小角的4倍，另外一个角是60°，这个三角形中最小的角是多少度？【思路引导】根据三角形的内角和等于180°，解答此题即可。【完整解答】解：（180﹣60）÷（1+4）＝120÷5＝24（度）答：这个三角形中最小的角是24度。【考察注意点】熟练掌握三角形的内角和知识，是解答此题的关键。22．（5分）（2021春•德州期中）王老师准备了12厘米和6厘米的木棒各一根，现在他想拼成一个三角形，这个三角形第三边最长是多少厘米？最短是多少厘米？（取整厘米）【思路引导】任意三角形的两边之和必须大于第三边，任意两边的差必须小于第三边，据此解答。【完整解答】解：12+6＝18（厘米）12﹣6＝6（厘米）根据三角形的三边关系，因此三角形的第三边必须在6和118之间，因此最长是：18﹣1＝17（厘米），最短是6+1＝7（厘米）。答：这个三角形第三边最长是17厘米，最短是7厘米。【考察注意点】本题考查了三角形的三边关系的应用。23．（5分）（2021春•景县期中）一个等腰三角形的顶角是48°，那么它的一个底角是多少度？【思路引导】一个等腰三角形两个底角相等，三角形的内角和是180度，利用180度减去顶角的度数就是两个底角的度数和，再除以2即可求出一个底角的度数。【完整解答】解：（180°﹣48°）÷2＝132°÷2＝66°答：它的一个底角是66°。【考察注意点】本题考查了三角形内角和定理和等腰三角形的特征，属于基础题，关键是掌握三角形内角和为180度。24．（5分）（2021春•衡阳期末）向阳小学要举行一次风筝比赛。设计要求这个风筝的造型是等腰三角形，它的一个底角是42°，计算一下这个风筝的顶角是多少度？【思路引导】根据三角形的内角和等于180°和等腰三角形的两个底角相等，解答此题即可。【完整解答】解：180°﹣42°×2＝180°﹣84°＝96°答：这个风筝的顶角是96度。【考察注意点】熟练掌握三角形的内角和定理，是解答此题的关键。25．（6分）（2021春•铜官区期末）学校举行风筝比赛，李东做了一个风筝，风筝的造型是等腰三角形。其中有一个角是48°，其它两个角各是多少度？【思路引导】根据三角形的内角和等于180°和等腰三角形的两个底角相等，解答此题即可。【完整解答】解：假设这个角是顶角，则其它两个角：（180°﹣48°）÷2＝132°÷2＝66°假设这个角是底角，则另一个底角也是48°顶角：180°﹣48°×2＝180°﹣96°＝84°答：其它两个角是66°、66°或48°、84°。【考察注意点】熟练掌握三角形的内角和定理，是解答此题的关键。六．解答题（共7小题，满分29分）26．（3分）（2021春•河西区期末）下面的三角形有一个角被信封盖住了，猜一猜它们分别是什么三角形。【思路引导】据直角三角形的意义，有一个角是直角的三角形叫直角三角形；根据钝角三角形的意义，用一个角是钝角的三角形叫钝角三角形；根据锐角三角形的意义，三个角都是锐角的三角形叫锐角三角形；由此可以求出三角形的另外一个角的度数，进而根据锐角、直角、钝角三角形的含义进行判定。【完整解答】解：180﹣40﹣25＝115（度），所以该三角形是钝角三角形；180﹣18﹣72＝90（度），所以该三角形是直角三角形；180﹣65﹣65＝50（度），所以该三角形是锐角三角形；填写如下：【考察注意点】明确三角形按角分类的方法，是解答此题的关键。27．（3分）（2022春•科左中旗期中）请在三角形指定边上作高。【思路引导】过三角形指向底的对角顶点向指定底（或指定底所在的直线）作垂线，顶点与垂足间的线段，就是三角形指定底上的高。用三角板即可画出三角形的高。【完整解答】解：【考察注意点】本题是考查作三角形的高。注意作高通常用虚线，并标出垂足。28．（4分）（2022春•肇州县校级期中）∠1、∠2、∠3是一个三角形的内角，∠2是∠1的3倍，∠3是∠1的5倍，∠1、∠2、∠3分别是多少度？【思路引导】根据三角形的内角和等于180°，解答此题即可。【完整解答】解：180÷（3+5+1）＝180÷9＝20（度）20×3＝60（度）20×5＝100（度）答：∠1是20°、∠2是60°、∠3是100°。【考察注意点】熟练掌握三角形的内角和，是解答此题的关键。29．（4分）（2020春•柯桥区期末）如图1所示，一个三角形的三个角可以拼成一个平角，得知三角形的内角和是180°。我们发现：∠4＝∠2+∠3，你能根据这个发现，求出如图2中五个角的和吗？∠1+∠2+∠3+∠4+∠5＝　180　°写出你的思考过程：　∠1所在的小三角形的另外两个角分别等于∠2+∠3和∠4+∠5，这个小三角形内角和是180°，那么∠1+∠2+∠3+∠4+∠5＝180°。　。【思路引导】根据图1，与三角形的一个角拼成平角的角（我们叫它三角形的外角），等于与它不相邻的两个内角的和。∠1所在的小三角形的另外两个角分别等于∠2+∠3和∠4+∠5，这个小三角形内角和是180°，所以∠1+∠2+∠3+∠4+∠5＝180°。【完整解答】解：图中∠6＝∠4+∠5，∠7＝∠2+∠3∠1、∠7、∠6是同一个三角形的三个内角∠1+∠2+∠3+∠4+∠5＝∠1+∠7+∠6＝180°故答案为：180°，∠1所在的小三角形的另外两个角分别等于∠2+∠3和∠4+∠5，这个小三角形内角和是180°，那么∠1+∠2+∠3+∠4+∠5＝180°。【考察注意点】此题重点考查三个内角和为180°的运用。30．（5分）（2013春•双峰县期末）找规律，写得数．．（1）多边形内角和与它的边数的关系式是：（多边形边数﹣2）×　180　度．（2）一个十边形的内角和是　1440　度．【思路引导】（1）根据过同一顶点作出的对角线把多边形分成的三角形的个数的规律，再利用三角形的内角和等于180°即可推出多边形的内角和公式；（2）根据前面推出的公式代入计算即可求解．【完整解答】解：（1）n边形分成（n﹣2）个三角形，故多边形内角和与它的边数的关系式是：（多边形边数﹣2）×180度． （2）一个十边形的内角和是（10﹣2）×180°＝1440°答：一个十边形的内角和是1440度．故答案为：180，1440．【考察注意点】本题考查了多边形的内角和公式的推导，理清过同一个顶点把多边形分成的三角形的个数是解题的关键，也是本题的难点．31．（5分）（2021春•美兰区校级期末）一个直角三角形中，已知其中一个锐角是55，求另一个锐角是多少度？【思路引导】根据三角形的内角和公式，用“180﹣90＝90”求出直角三角形的另外两个内角的度数和，然后根据给出的一个锐角的度数，求出另外一个内角的度数．【完整解答】解：180﹣90﹣55，＝90﹣55，＝35（度）．答：另一个锐角是35度．【考察注意点】此题考查了三角形的内角和，应注意知识的灵活运用．32．（5分）（2020春•越城区期末）已知三角形的两条边长分别是1cm和2cm，那么第三条边长可能是多少？为什么？（取整厘米数）【思路引导】根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可。【完整解答】解：2﹣1＜第三边＜2+1所以1＜第三边＜3所以第三边的长是2厘米。答：第三边的长是2厘米。【考察注意点】此题关键是根据三角形的特性进行分析、解答即可