初中数学8.2 消元---解二元一次方程组试讲课ppt课件

课题名

8.2.1  代入法解二元一次方程组

教学目标

1.了解解二元一次方程组时的“消元思想”,“化未知为已知”的化归思想.

2.会用二元一次方程组解决实际问题。

教学重点

理解“消元思想”和“化归思想”

教学难点

会用代入法解二元一次方程组

教学准备

教师准备：PPT

学生准备：听课笔记，习题本

教学过程

教学流程

教师活动

学生活动

设计意图

新课导入

师：上节课我们学习了二元方程及二元一次方程组的有关知识，同学们请回答以下3个问题。

《一千零一夜》中有这样一段文字：有一群鸽子，其中一部分在树上，另一部分在地上．树上的一只鸽子对地上的鸽子说：“若从你们中飞上来一只，则地上的鸽子为整个鸽群的三分之一；若从树上飞下去一只，则树上、地上的鸽子一样多．”你知道树上、地上各有多少只鸽子吗？

方法一：设树上有x只鸽子，则由题意得：x+(x-2)=3[(x-2)-1]

方法二：解：设树上有x只鸽子，地上有y只鸽子，

               得到方程组

1、什么叫二元一次方程组的解？

2、若是方程2x+y=2的解，则8a+4b-3=____.

．已知4x-y=-1，用关于x的代数式表示y：___________；

用关于y的代数式表示x ：_________

 此题怎么解呢？有几种解法？

我们发现，二元一次方程组中第二个方程可以写出y=x-2.由于两个方程中的y都表示地上鸽子的数量，所以我们把第一个方程中的y都换成x-2，这个方程组就转化为一元一次方程x+(x-2)=3[(x-2)-1]，解这个方程即可得出x的值，然后再代入y=x-2，即可得出y的值.

复习，为新知学习做好准备。

引入新课。

通过实际应用，发现二元一次方程组的价值，并思考如何求出方程组的解。

关注两种数量关系，得出两个方程。

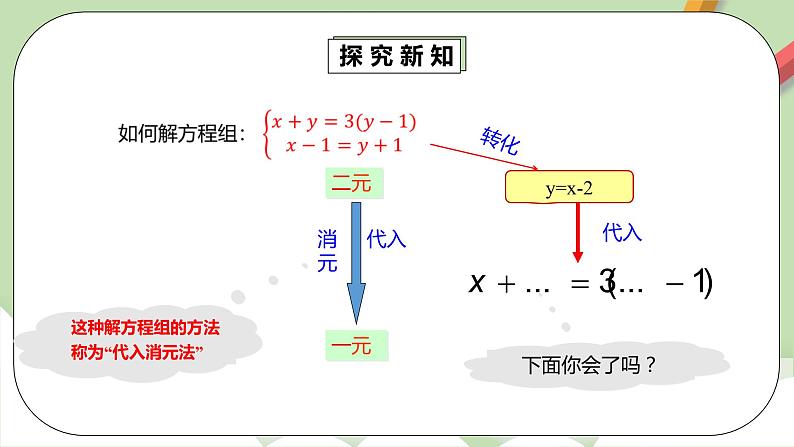
探究新知

师：根据上面的问题，我们思考如何求解。

二元一次方程组中有两个未知数，如果消去其中一个未知数，将二元一次方程组转化为我们熟悉的一元一次方程，我们就可以先解出一个未知数，然后再设法求另一未知数.这种将未知数的个数由多化少、逐一解决的思想，叫做消元思想.

把二元一次方程组中一个方程的一个未知数用含有另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解，这种方法叫做代入消元法，简称代入法.

    理解消元思想

解方程组时，将未知数的个数由多化少、逐一解决的思想，叫消元思想.

    代入消元法简称，代入法。

明确探究范围，强调“相交”。

培养学生的学科素养。

强化基础知识，培养学科素养。

归纳总结探究的结果。

典例剖析

例1：解方程组

学生独立解答此题并总结步骤.

方法提炼

用代入法解二元一次方程组的一般步骤

1.将方程组里的一个方程变形，用含有一个未知数的式子表示另一个未知数；

2.用这个式子代替另一个方程中相应的未知数，得到一个一元一次方程，求得一个未知数的值；

3.把这个未知数的值代入上面的式子，求得另一个未知数的值；

4、写出方程组的解

跟踪训练

回答：

把③代入②可以吗？

把y=2代入① 或②可以吗？

把求出的解代入原方程组，可以知道你解得对不对.

典例剖析

例2、用代入法解方程组

解：令,则x=3k+2 ③ y=5k-4 ④

把③、④代入，得2(3k+2)-7(5k-4)=90

解得：k=-2

即=-2，

解得：

跟踪练习

已知是关于x，y的方程组的解，求a，b的值.

典例剖析

例3、根据市场调查，某种消毒液的大瓶装（500g）和小瓶装（250g），两种产品的销售数量（按瓶计算）的比为2:5某厂每天生产这种消毒液22.5吨，这些消毒液应该分装大、小瓶两种产品各多少瓶？

根据题意可列方程组：

由得：

把③代入得：

解得：x=20000

把x=20000代入得：y=50000

答：这些消毒液应该分装20000大瓶和50000小瓶.

链接中考

(中考，河北)如图4-2所示的两架天平保持平衡，且每块巧克力的质量相等，·每个果冻的质量也相等，则一块巧克力的质量是(     )

A.20g           B.25g           C.15g           D.30g

随堂检测

1．在方程2x－3y＝6中，用含有x的代数式表示y，得（   ）

A.

C.

2.用代入法解方程组下列说法正确的是(     )

A．直接把①代入②，消去y

B．直接把①代入②，消去x

C．直接把②代入①，消去y

D．直接把②代入①，消去x

3．二元一次方程组的解为(     )

A.                     B.

C.                     D.

4．方程组的解为____________．

5．用代入法解下列方程组：

6.小张把两个大小不同的苹果放到天平上称，当天平保持平衡时的砝码重量如图所示．问：这两个苹果的重量分别为多少克？

课堂小结

1.解二元一次方程组的基本思想是什么？（消元）

2.我们已经学习了解二元一次方程组的哪些知识？

教学反思

在这节课的教学过程中，对学生的学习积极性调到不够，整个课堂气氛较和谐，因为课前已经做了充分准备，所以整节课教学过程流畅，讲解例题时由简单到复杂，由易到难逐步加深。解二元一次方程组的基本思想是消元，学生能较好地用含有一个未知数的式子。