陕西省西安市周至县第四中学2022-2023学年高三上学期期中考试数学（理）试题

2022-2023学年度第一学期

高三数学（理科）期中考试题

考试时间：120分钟    总分：150分

第I卷（选择题）

一、单选题（每题只有一个正确选项，每题5分，共70分）

2．设，，，则的大小关系为（    ）

A． B． C． D．

3．函数零点所在的一个区间是（    ）

A． B． C． D．

4．已知命题p：，，命题q：，，则下列判断正确的是（    ）

A．是假命题    B．q是真命题   C．是真命题  D．是真命题5．“”是“”的（    ）

A．充分不必要条件 B．充要条件

C．必要不充分条件 D．既不充分也不必要条件

6．下列函数中，既是偶函数又在区间上单调递增的是（    ）

A． B． C． D．

7．函数在区间上的最小值是（    ）

A．- B． C．1 D．-1

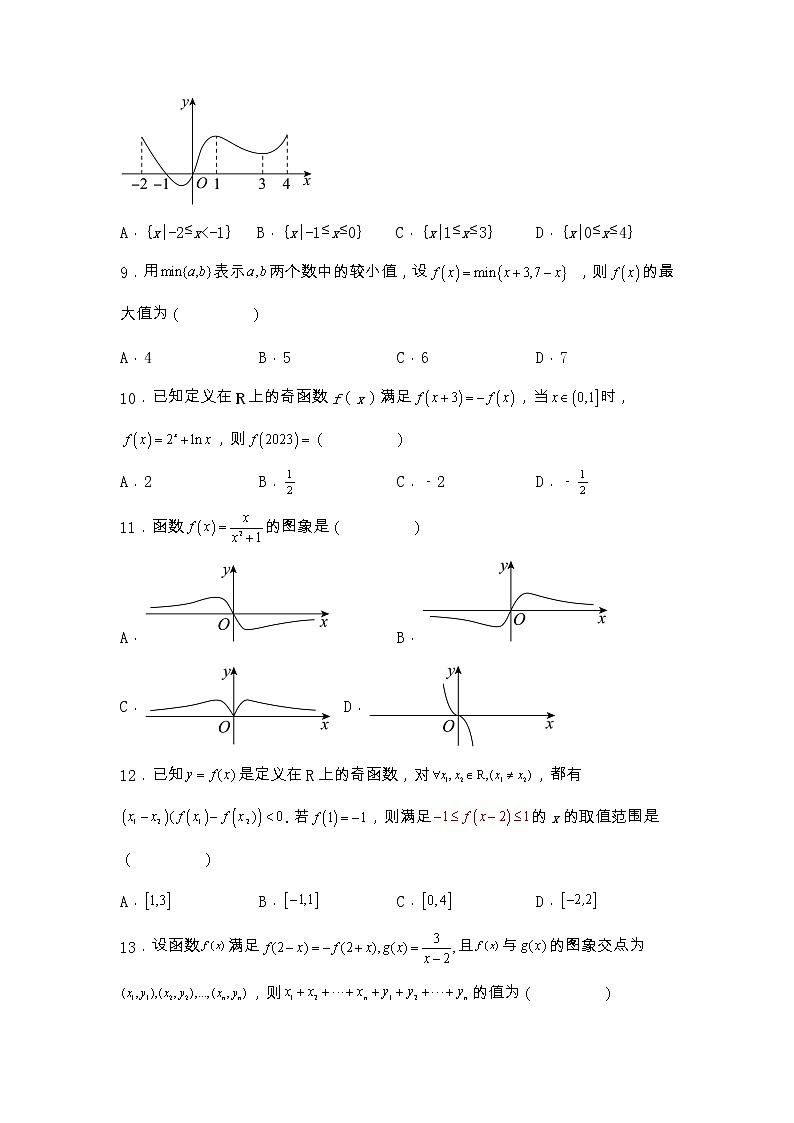
8.已知函数f(x)的定义域为[-2，4]，其图像如图所示，则xf(x)<0的解集为（    ）

A．{x|-2≤x<-1}   B．{x|-1≤x≤0}    C．{x|1≤x≤3}    D．{x|0≤x≤4}

9．用表示两个数中的较小值，设 ，则的最大值为（    ）

A．4 B．5 C．6 D．7

10．已知定义在R上的奇函数f（x）满足，当时，，则（    ）

A．2 B． C．－2 D．－

11．函数的图象是（    ）

A． B．

C． D．

12．已知是定义在R上的奇函数，对，都有.若，则满足的x的取值范围是（    ）

A． B． C． D．

13．设函数满足且与的图象交点为，则的值为（    ）

A．0 B．n C．2n D．4n

14．已知函数，则不等式的解集为（    ）

A． B． C． D．

第II卷（非选择题）

二、填空题（每题5分，共30分）

15．,的否定形式为__________.

17．函数的单调递增区间是__．

18．已知，则__________.

19．若函数的零点是和，则不等式的解集为__________.

三、解答题（请规范书写必要的解题步骤）

21．（10分）化简求值：

(1)；

(2)．

22．（10分）解下列不等式和方程：

（1）

（2）

23．（15分）已知函数f(x)＝，若函数f(x)的图像过点(－1，3)．

(1)求k的值；

(2)若f(a)≥27，求实数a的取值范围；

(3)若函数y＝f(|x|)－b有两个零点，求实数b的取值范围．

24．（15分）已知函数是上的奇函数，当时，．

（1）当时，求的解析式；

（2）若，求实数的取值范围．

高三数学（理科）期中考试答案

一、单选题（每题只有一个正确选项，每题5分，共70分）

1.D   2.D   3.C   4.D    5.C   6.C   7.A    8.A   9.B   10.A

11.B    12.A     13.C    14.D

二、填空题（每题5分，共30分）(对一空得3分）

15．,      16.         17．          18．            19．              20 .m=-1 ,    n=2

三、解答题（请规范书写必要的解题步骤）共50分

21．（10分）化简求值：

(1)；

(2)．

【解析】（1）根据有理数指数幂及根式的运算性质即可求解；

（2）根据对数运算性质及指数幂的运算即可求解.

【详解】（1）原式，

（2）原式

.

22．（10分）解下列不等式和方程：

（1）

（2）

解答：（1），（2）或

【分析】（1）利用对数函数的单调性解不等式即可；

（2）利用换元法，设，则，求出的值，从而可求出的值

【详解】解：（1）由，得，

所以，解得，

所以不等式的解集为，

（2）设，则，得，

解得或，

当时，，得，

当时，，得，

所以方程的解为或

23．（15分）已知函数f(x)＝，若函数f(x)的图像过点(－1，3)．

(1)求k的值；

(2)若f(a)≥27，求实数a的取值范围；

(3)若函数y＝f(|x|)－b有两个零点，求实数b的取值范围．

解：(1)∵f(－1)＝3，

∴＝3，

∴k－2＝－1，解得k＝1.

(2)由(1)及题意得，f(a)＝≥27，

∴2a＋1≤－3，

解得a≤－2.

故实数a的取值范围为(－∞，－2]．

(3)由(1)知，f(x)＝，∴当x≥0时，

f(|x|)＝是减函数，值域为.

∵y＝f(|x|)是偶函数，

∴当x≤0时，y＝f(|x|)是增函数，值域为，

∴函数y＝f(|x|)－b有两个零点时，b∈.

24．（15分）已知函数是上的奇函数，当时，．

（1）当时，求的解析式；

（2）若，求实数的取值范围．

答案（1）；（2）．

【分析】（1）根据题意，当时，，求出的表达式，结合函数的奇偶性的解析式，即可得答案；

（2）根据题意，分析函数在上的单调性，则原不等式等价于，进而可得，解可得的取值范围，即可得答案．

【详解】（1）根据题意，当时，，则，

又由是上的奇函数，则，

故；

（2）当时，，则在上为增函数，

又由是上的奇函数，则在上也为增函数，

由于函数在处连续，故在上为增函数，

由可得，

，解得.

因此，实数的取值范围是.