资料中包含下列文件,点击文件名可预览资料内容





还剩3页未读,
继续阅读
成套系列资料,整套一键下载
- 专题15 整式加减运算特训50道 其他 5 次下载
- 专题16 整式加减中的化简求值特训50道 其他 9 次下载
- 专题18 一元一次方程有整数解 其他 4 次下载
- 专题19 同解方程 其他 5 次下载
- 专题20 解一元一次方程特训50道 其他 8 次下载
专题17 整式加减的应用
展开
专题17 整式加减的应用
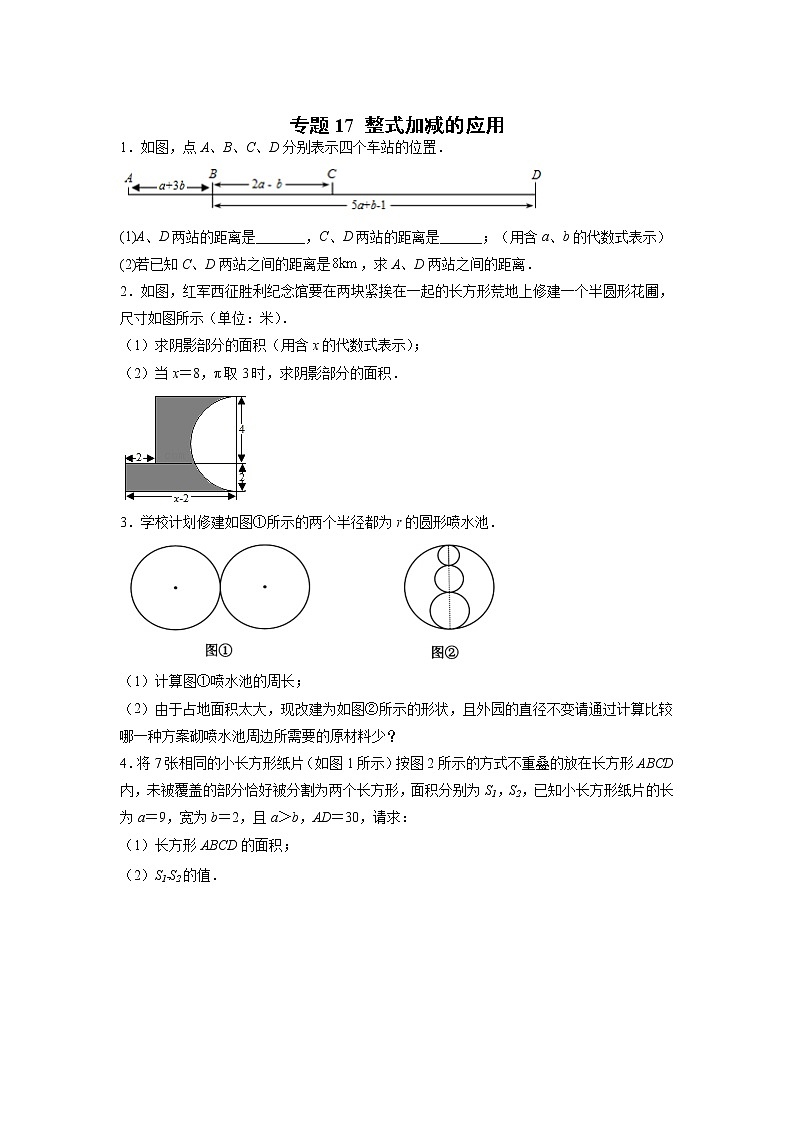
1.如图,点A、B、C、D分别表示四个车站的位置.
(1)A、D两站的距离是_______,C、D两站的距离是______;(用含a、b的代数式表示)
(2)若已知C、D两站之间的距离是,求A、D两站之间的距离.
【答案】(1)6a+4b-1,3a+2b-1
(2)A,D两站之间的距离为17km
【分析】(1)根据和代入求解即可;
(2)首先根据代入(1)中求出的中得到关于AB的等式,然后整体代入到(1)中求出的中即可求解.
(1)
解:,
,
故答案为:6a+4b-1,3a+2b-1.
(2)
解:∵CD=8,
∴3a+2b-1=8,
∴3a+2b=9,
∴AD=6a+4b-1=2(3a+2b)-1=2×9-1=17.
答:A,D两站之间的距离为17km.
【点睛】此题考查了线段的和差运算,整式的加减混合运算的应用,代数式求值问题,解题的关键是熟练掌握整式的加减混合运算法则和整体代入思想的运用.
2.如图,红军西征胜利纪念馆要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,尺寸如图所示(单位:米).
(1)求阴影部分的面积(用含x的代数式表示);
(2)当x=8,π取3时,求阴影部分的面积.
【答案】(1)6x﹣20﹣π;(2)13.5.
【分析】(1)利用两个长方形的面积之和减去半圆的面积即可;
(2)将x=8,π取3代入(1)中的代数式计算即可.
【详解】解:(1)阴影部分的面积为:
2(x﹣2)+4(x﹣2﹣2)﹣×π×32
=6x﹣20﹣π.
∴阴影部分的面积为(6x﹣20﹣π);
(2)当x=8,π取3时,
6x﹣20﹣4.5π
=6×8﹣20﹣4.5×3
=28﹣13.5
=14.5.
答:阴影部分的面积为13.5.
【点睛】本题考查了整式的加减的应用,正确的列出代数式是解题的关键.
3.学校计划修建如图①所示的两个半径都为r的圆形喷水池.
(1)计算图①喷水池的周长;
(2)由于占地面积太大,现改建为如图②所示的形状,且外园的直径不变请通过计算比较哪一种方案砌喷水池周边所需要的原材料少?
【答案】(1);(2)经过计算可得两种方案的周长相等,因此两种方案所需要的原材料相等
【分析】(1)直接根据圆的周长公式进行求解即可;
(2)设这个喷水池内圆半径分别为,则方案②的周长,进而问题可求解.
【详解】解:(1)因为这个喷水池由两个半径为圆形图案组成,
所以这个喷水池的周长为;
(2)设这个喷水池内圆半径分别为,
则方案②的周长
所以,经过计算可得两种方案的周长相等,因此两种方案所需要的原材料相等.
【点睛】本题主要考查列代数式及整式的加减,熟练掌握列代数式及整式的加减是解题的关键.
4.将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a=9,宽为b=2,且a>b,AD=30,请求:
(1)长方形ABCD的面积;
(2)S1﹣S2的值.
【答案】(1)510;(2).
【分析】(1)先用含a和b的式子表示出CD的长,然后求得矩形ABCD的面积,从而代入求值;
(2)根据长方形的面积公式列式,然后代入求值.
【详解】(1)①由题意可得:CD=a+4b,
∴S长方形ABCD=AD•CD=AD(a+4b),
当a=9,b=2,AD=30时,
S长方形ABCD=30×(9+4×2)=30×17=510,
故长方形ABCD的面积为:510;
②由题意可得:S2=a(AD−3b),S1=4b(AD−a),
当a=9,b=2,AD=30时,
=
=
=
=.
【点睛】此题考查了整式的加减运算以及代数式求值问题,熟练掌握运算法则是解本题的关键.整式加减的应用时:(1)认真审题,弄清已知和未知的关系;(2)根据题意列出算式.
5.已知:b是最小的正整数,且a、b、c满足(c﹣5)2+|a+b|=0,请回答问题:
(1)请直接写出a、b、c的值.a=_____ ,b= ______ ,c= ______
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|﹣|x﹣1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值
【答案】(1) -1;1;5;(2) 4x+10或2x+12;(3)不变, BC-AB=2
【分析】(1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数的和是0,则每个数都是0,即可求得a,b,c的值;
(2)根据x的范围,确定x+1,x-1,x+5的符号,然后根据绝对值的意义即可化简;
(3)先求出BC=3t+4,AB=3t+2,从而得出BC-AB=2.
【详解】(1)∵b是最小的正整数,∴b=1.
根据题意得:c-5=0且a+b=0,
∴a=-1,b=1,c=5.
故答案是:-1;1;5;
(2)当0≤x≤1时,x+1>0,x-1≤0,x+5>0,
则:|x+1|-|x-1|+2|x+5|
=x+1-(1-x)+2(x+5)
=x+1-1+x+2x+10
=4x+10;
当1<x≤2时,x+1>0,x-1>0,x+5>0.
∴|x+1|-|x-1|+2|x+5|
=x+1-(x-1)+2(x+5)
=x+1-x+1+2x+10
=2x+12.
(3)不变.理由如下:
t秒时,点A对应的数为-1-t,点B对应的数为2t+1,点C对应的数为5t+5.
∴BC=(5t+5)-(2t+1)=3t+4,AB=(2t+1)-(-1-t)=3t+2,
∴BC-AB=(3t+4)-(3t+2)=2,
即BC-AB的值不随着时间t的变化而改变,BC-AB=2.
【点睛】本题考查了数轴与绝对值,整式的加减,通过数轴把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.
6.小明的爸爸以每件m元的成本价购进了30件甲种商品,以每件n元的成本价购进了40件乙种商品,且.
(1)在销售前小明的爸爸经市场调查发现,甲种商品比较畅销供不应求,乙种商品基本没人问津.为了尽快减少库存,但又不能亏本,小明的爸爸决定将甲种商品按成本价提高40%后标价出售;乙种商品按成本价的七折出售,则甲种商品的每件售价可表示为______(用含m的代数式表示),乙种商品的每件售价可表示为______(用含n的代数式表示);
(2)在(1)的条件下,将甲、乙商品全部售出,用含m、n的代数式表示小明爸爸的获利;
(3)若小明的爸爸将两种商品都以的平均价格一次打包全部出售,请判断他这次买卖是赚钱还是亏本,请说明理由.
【答案】(1),;(2);(3)赚钱,理由见解析
【分析】(1)根据甲种商品按成本价提高40%后标价出售;乙种商品按成本价的七折出售解答即可;
(2)根据总销售额减去总成本即可得出总获利;
(3)利用已知表示出总销售额减去总成本,判断正负即可得出结论.
【详解】解:(1)由题意得:甲种商品的每件售价为:,
乙种商品的每件售价为:,
故答案为:,;
(2)由题意得:,
故总获利为:;
(3)根据题意,这次买卖的利润为:,
∵,
∴,
∴,
∴这次买卖是赚钱.
【点睛】本题考查了列代数式以及整式的加减运算,正确表示出获利是解题的关键.
7.某超市在双十一期间对购物实行优惠,规定如下:
一次性购物货款
优惠办法
不超过200元
不予优惠
超过200元但不超过500元
九折优惠
超过500元
其中500元部分给予九折优惠,超过500元部分给予八折优惠
(1)王阿姨一次性购物700元,她实际付款 元.
(2)若顾客在该超市一次性购物货款为x元,用含x的代数式表示下列结果.
①当x超过200元但不超过500元时,实际付款 元;
②当x大于500元时,实际付款 元.
(3)如果王阿姨两次购物货款合计840元,第一次购物的货款为元(200<<300),用含的代数式表示:王阿姨两次购物实际付款一共多少元?
【答案】(1)610;(2)①0.9x;②0.8x+50;(3)0.1a+722
【分析】(1)让500元部分按9折付款,剩下的200元按8折付款即可;
(2)①当x超过200元但不超过500元时,实际付款=购物款×9折;
②当x大于500元时,实际付款=500×9折+超过500的购物款×8折;
(3)两次购物王阿姨实际付款=第一次购物款×9折+500×9折+(总购物款-第一次购物款-第二次购物款500)×8折,把相关数值代入即可求解.
【详解】解:(1)根据题意得,王阿姨一次性购物700元,实际付款:
500×0.9+(700-500)×0.8=610(元).
故答案为:610;
(2)若顾客在该超市一次性购物x元,
①当x超过200元但不超过500元时,实际付款0.9x元;
②当x大于500元时,实际付款500×0.9+0.8(x-500)=(0.8x+50)元.
故答案为:0.9x,(0.8x+50);
(3)根据题意可得:
两次购物王阿姨实际共付款:
0.9a+0.8(840-a-500)+500×0.9
=0.9a+0.8(340-a)+450
=0.1a+722.
答:两次购物王阿姨实际付款(0.1a+722)元.
【点睛】本题考查了列代数式以及整式加减的应用,解决本题的关键是得到不同购物款所得的实际付款的等量关系,难点是求第二问的第二次购物款应分9折和8折两部分分别计算实际付款.
8.如图,用三种大小不同的六个正方形和一个缺角的长方形拼成大长方形ABCD,其中 GH =1,HM =3,设BF=a
(1)用含a的代数式表示CN= cm,DN= cm
(2)用含a的代数式表示大长方形ABCD的周长
【答案】(1)(a+1),3a;(2)18a+8
【分析】(1)根据正方形的性质和线段的和差关系即可得出CN和DN,
(2)先求出长方形ABCD的长和宽,再用2×(长+宽)即可得出长方形ABCD的周长.
【详解】(1)CN=BF+HG=a+1,
DN=MN=NH-MH
=3NC-MH
=3×(a+1)-3
=3a;
(2)DC=CN+DN=a+1+3a=4a+1
BC=a×2+(a+1)×3=2a+3a+3=5a+3
C长ABCD=(4a+1+5a+3)×2
=18a+8.
【点睛】此题考查了列代数式和整式的加减,主要是能够用不同的方法表示同一个长方形的宽,注意各个正方形的边长之间的数量关系.
9.如图,用三种大小不同的5个正方形和1个长方形(阴影部分)拼成长方形ABCD,其中EF=3,最小的正方形的边长为x.
(1)FG= ,DG= ;(用含x的代数式表示)
(2)用含x的代数式表示长方形ABCD的周长,并求当x=6时长方形ABCD的周长.
【答案】(1)x+3,3x﹣3;(2)16x+6,102
【分析】(1)根据正方形的性质及线段的和差关系即可表示出FG和DG;
(2)先表示出长方形ABCD的长和宽,再表示出长方形的周长,把x=6代入即可求出答案.
【详解】解:(1)根据图形可知:
FG=x+3,
DG=HF=3x﹣EF=3x﹣3,
故答案为:x+3,3x﹣3;
(2)∵长方形的宽为:x+3+3x﹣3=4x,长方形的长为:3x+x+3=4x+3,
∴长方形ABCD的周长为:[4x+(4x+3)]×2=16x+6,
当x=6时,16x+6=16×6+6=102.
【点睛】本题考查了列代数式及代数式求值,理解各个正方形的边长之间的数量关系是解决问题的关键.
10.定义:若,则称与是关于的平衡数.
例如:若,则称与是关于3的平衡数.
(1)①2 与 是关于3的平衡数;
② 与 是关于3 的平衡数. (用含的代数式表示).
(2)若,判断与是否是关于0 的平衡数,并说明理由.
【答案】(1)①1,②;(2)a与b不是关于0的平衡数,理由见解析
【分析】(1)①根据平衡数的定义列式计算即可;
②根据平衡数的定义列式计算即可;
(2)首先去括号,合并同类项化简a,b,然后计算a+b的值即可进行判断.
【详解】解:(1)①∵3-2=1,
∴2与1是关于3的平衡数;
②∵3-(4-x)=3-4+x=x-1,
∴4-x与x-1是关于3的平衡数;
(2)
,
∵
∴a与b不是关于0的平衡数.
【点睛】本题考查了整式加减的实际应用,正确理解平衡数的定义是解题关键.
11.某超市在春节期间对顾客实行优惠,规定如下:
一次性购物
优惠办法
少于200元
不予优惠
低于500元但不低于200元
九折优惠
500元或超过500元
其中500元部分给予九折优惠,超过500元部分给予八折优惠
(1)王老师一次性购物650元,他实际付款 元.
(2)若顾客在该超市一次性购物元,当小于500元但不小于200元时,他实际付款 元,当大于或等于500元时,他实际付款 元.(用含的代数式表示)
(3)如果王老师两次购物货款合计810元,第一次购物的货款为元,用含的代数式表示:两次购物王老师实际共付款多少元?(要求列式并化简)
【答案】(1)570;(2),;(3)或元
【分析】(1)500元的部分按9折付款,剩下的150元按原价付款即可;
(2)当x小于500元但不小于200元时,实际付款=购物款×9折,当x大于或等于500元时,实际付款=500×9折+超过500的购物款×8折;
(3)分两种情况:a<200和200≤a<300分别计算,即可得出结果.
【详解】解:(1)根据题意得:
(元,
故答案为:570;
(2)若顾客在该超市一次性购物元,
当小于500元但不小于200元时,实际付款:元,
当大于或等于500元时,实际付款:,
故答案为:,;
(3)当时,两次购物王老师实际共付款:元,
当时,两次购物王老师实际共付款:元,
两次购物王老师实际共付款或元.
【点睛】本题考查了列代数式及求值,根据不同情况正确列出代数式是解决问题的关键.
12.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、b满足.
(1)______,______,______;(直接写得数)
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合(请写出过程);
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则______,______,______.(直接用含t的代数式表示)
(4)请问:的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1),1,7;(2)4,见解析;(3),,;(4)不变,12
【分析】(1)由非负数的性质可得,,从而求解的值,再由b是最小的正整数求解即可;
(2)先求解对折时折痕点对应的数,再计算与折痕点之间的距离即可得到答案;
(3)先表示运动后对应的数分别为: 再利用数轴上两点之间的距离公式进行计算可得答案;
(4)结合(3)问的结论计算,根据计算的结果进行作答即可.
【详解】解:(1)因为,
所以,,
所以,.
又因为b是最小的正整数,所以,,
答案:,,.
(2)由折痕点是线段AC的中点,
折痕点对应的数为:
对应的数为
点B与数4表示的点重合
故答案为:4.
(3)由题意可得:运动后对应的数分别为:
,
.
(4)解:不变.理由如下:
.
为定值,不会发生变化.
【点睛】本题考查的是数轴上两点之间的距离,绝对值非负性的应用,数轴上线段的中点对应的数的表示,列代数式,整式的加减运算的应用,掌握以上基础知识是解题的关键.
13.如图,正方形和正方形的边长分别为9和.
(1)写出表示阴影部分面积的代数式(结果要求化简);
(2)当时,求阴影部分的面积.
【答案】(1);(2)
【分析】(1)阴影部分面积两个正方形面积和减去两个直角三角形面积,把对应的三角形面积代入即可;
(2)直接把代入(1)中可求出阴影部分的面积.
【详解】解:(1),
;
(2)当时,
,
阴影部分的面积为.
【点睛】本题考查列代数式.准确把握图形间的关系,找到阴影部分的面积是哪些规则图形的面积差是解题的关键.
14.某商场销售一种西装和领带,西装每套定价1000元,领带每条定价200元.“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款 元.(用含x的代数式表示)若该客户按方案二购买,需付款 元.(用含x的代数式表示)
(2)若x=32,通过计算说明此时按哪种方案购买较为合算?
(3)当x=32时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
【答案】(1),;(2)方案一合算;(3)先按方案一购买20套西装并获赠20条领带,再按方案二购买12条领带,则需22160元.
【分析】(1)方案①付费为:套西装的价钱条领带的钱;方案②付费为:(套西装的钱+条领带的钱)×;
(2)将代入(1)中的代数式,分别计算即可;
(3)只买套西装按方案①付费,剩下的领带按折付费.
【详解】解:(1)方案①付费为:,
方案②付费为:,
故答案为:,;
(2)若x=32,则方案①付费为:元,
方案②付费为:元,
∵,
∴则方案①购买较合算;
(3)只买套西装按方案①付费,得到获赠的条领带,剩下的领带按折付费,
总费用为:元.
【点睛】本题考查了列代数式以及代数式求值,得到所给方案计算的等量关系是解决本题的关键.
15.某水果经销户从水果市场批发了苹果和桔子共100千克,苹果和桔子当天的批发价、零售价如下表:
品 名
苹 果
桔 子
批发价(元/ kg)
5.2
3.2
零售价(元/ kg)
8.8
6.2
(1)若经销户分别批发了60 kg苹果和40 kg桔子,那么当天卖完这些苹果和桔子该经销户能盈利 元.
(2)若经销户批发了m kg苹果,当天卖完这些苹果和桔子经销户能盈利多少元?(用含m的代数式表示,要求化简)
【答案】(1)336;(2)0.6m+300.
【分析】(1)根据题意可得利润为60×(8.8-5.2)+40×(6.2-3.2),进而计算即可求得答案;
(2)根据题意可得利润为m·(8.8-5.2)+(100-m)×(6.2-3.2),进而化简即可求得答案.
【详解】解:(1)根据题意可得:
60×(8.8-5.2)+40×(6.2-3.2)
=60×3.6+40×3
=216+120
=336(元),
故答案为:336 ;
(2)根据题意可得:
m·(8.8-5.2)+(100-m)×(6.2-3.2)
=3.6m+3(100-m)
=3.6m+300-3m
=0.6m+300.
【点睛】本题考查了有理数的混合运算以及整式加减的实际应用,熟练掌握整式加减的运算法则是解决本题的关键.
16.某电器商销售一种微波炉和电磁炉,微波炉每台定价900元,电磁炉每台定价300元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的80%付款.
现某客户要到该卖场购买微波炉2台,电磁炉x台(x>2).
(1)若该客户按方案一购买,需付款 元 (用含x的代数式表示) .
若该客户按方案二购买,需付款 元 (用含x的代数式表示) .
(2)若x=6时,通过计算说明此时按哪种方案购买较为合算?
(3)当x=6时,你能给出一种更为省钱的购买方案吗?试写出购买方案,并计算需要付款多少元?
【答案】(1)(300x+1200),(240x+1440);(2)按方案二购买较合算;(3)先按方案一购买2台微波炉送2台电磁炉,再按方案二购买4台电磁炉,共2760元.
【分析】(1)根据题目提供的两种不同的付款方式列出代数式即可;
(2)将x=6代入求得的代数式中即可得到费用,然后比较即可得到选择哪种方案更合算;
(3)根据题意考可以得到先按方案一购买2台微波炉再送2台电磁炉,再按方案二购买3台电磁炉更合算.
【详解】解:(1)方案一: ,
方案二: ;
故答案为:(300x+1200),(240x+1440);
(2)当x=6时,方案一:300×6+1200=3000(元),
方案二:240×6+1440=2880(元),
按方案二购买较合算;
(3)先按方案一购买2台微波炉送2台电磁炉,再按方案二购买4台电磁炉,
共2×900+300×4×80%=2760(元).
【点睛】本题考查了列代数式和求代数式的值的相关的题目,解题的关键是认真分析题目并正确的列出代数式.
17.某设计公司设计出如图所示的一个图案(图中阴影部分),其中长方形的长为,宽为y,扇形的半径为y.
(1)用含x、y的代数式表示图案(图中阴影部分)的面积S;
(2)当x=12,y=8时,求面积S的值.(结果保留π)
【答案】(1)xy+y2;(2)16π+16
【分析】(1)用矩形的面积加四分之一圆的面积减去大三角形的面积即可求出答案;
(2)将x=12,y=8代入求解即可.
【详解】(1)阴影部分的面积为
;
(2)当x=12,y=8时,
.
【点睛】本题主要考查整式加减的应用,掌握整式加减的运算法则是关键.
18.某超市在双十一期间对顾客实行优惠,规定如下:
一次性购物
优惠办法
少于200元
不予优惠
低于500元但不低于200元
八折优惠
500元或超过500元
其中500元部分给予八折优惠,超过500元部分给予七折优惠
(1)若王老师一次性购物600元,他实际付款______元.若王老师实际付款160元,那么王老师一次性购物可能是______元;
(2)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款_______元,当x大于或等于500元时.他实际付款_____元(用含x的代数式表示并化简);
(3)如果王老师有两天去超市购物原价合计850元,第一天购物的原价为a元(200<a<300),用含a的代数式表示:两天购物王老师实际一共付款多少元?当a=250元时.王老师两天一共节省了多少元?
【答案】(1)470元;200或160元;(2)0.8x;(0.7x+50);(3)共节省180元.
【分析】(1)根据表格中的数量关系,列出算式,即可;
(2)根据表格中的数量关系,列出代数式,即可;
(3)分别列出第一天购物和第二天购物的代数式,再求和,最后代入求值即可.
【详解】(1)解:王老师一次性购物600元,他实际付款:500×0.8+100×0.7=470(元),
王老师实际付款160元,那么王老师一次性购物可能是:160÷0.8=200元或160元
故答案是:470;200或160;
(2)顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款0.8x元;当x大于或等于500元时.他实际付款:(0.7x+50)元,
故答案是:0.8x;(0.7x+50);
(3)解:第一天购物实际付款:0.8a元,
第二天购物实际付款:500×0.8+0.7(850-a-500)=(645-0.7a)元,
两天共付款:(0.1a+645) 元,
当a=250元时,0.1a+645=670元;
所以共节省:850-670=180元.
【点睛】本题主要考查列代数式以及整式的加减运算,理解题目中的数量关系,列出代数式,是解题的关键.
专题17 整式加减的应用
1.如图,点A、B、C、D分别表示四个车站的位置.
(1)A、D两站的距离是_______,C、D两站的距离是______;(用含a、b的代数式表示)
(2)若已知C、D两站之间的距离是,求A、D两站之间的距离.
【答案】(1)6a+4b-1,3a+2b-1
(2)A,D两站之间的距离为17km
【分析】(1)根据和代入求解即可;
(2)首先根据代入(1)中求出的中得到关于AB的等式,然后整体代入到(1)中求出的中即可求解.
(1)
解:,
,
故答案为:6a+4b-1,3a+2b-1.
(2)
解:∵CD=8,
∴3a+2b-1=8,
∴3a+2b=9,
∴AD=6a+4b-1=2(3a+2b)-1=2×9-1=17.
答:A,D两站之间的距离为17km.
【点睛】此题考查了线段的和差运算,整式的加减混合运算的应用,代数式求值问题,解题的关键是熟练掌握整式的加减混合运算法则和整体代入思想的运用.
2.如图,红军西征胜利纪念馆要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,尺寸如图所示(单位:米).
(1)求阴影部分的面积(用含x的代数式表示);
(2)当x=8,π取3时,求阴影部分的面积.
【答案】(1)6x﹣20﹣π;(2)13.5.
【分析】(1)利用两个长方形的面积之和减去半圆的面积即可;
(2)将x=8,π取3代入(1)中的代数式计算即可.
【详解】解:(1)阴影部分的面积为:
2(x﹣2)+4(x﹣2﹣2)﹣×π×32
=6x﹣20﹣π.
∴阴影部分的面积为(6x﹣20﹣π);
(2)当x=8,π取3时,
6x﹣20﹣4.5π
=6×8﹣20﹣4.5×3
=28﹣13.5
=14.5.
答:阴影部分的面积为13.5.
【点睛】本题考查了整式的加减的应用,正确的列出代数式是解题的关键.
3.学校计划修建如图①所示的两个半径都为r的圆形喷水池.
(1)计算图①喷水池的周长;
(2)由于占地面积太大,现改建为如图②所示的形状,且外园的直径不变请通过计算比较哪一种方案砌喷水池周边所需要的原材料少?
【答案】(1);(2)经过计算可得两种方案的周长相等,因此两种方案所需要的原材料相等
【分析】(1)直接根据圆的周长公式进行求解即可;
(2)设这个喷水池内圆半径分别为,则方案②的周长,进而问题可求解.
【详解】解:(1)因为这个喷水池由两个半径为圆形图案组成,
所以这个喷水池的周长为;
(2)设这个喷水池内圆半径分别为,
则方案②的周长
所以,经过计算可得两种方案的周长相等,因此两种方案所需要的原材料相等.
【点睛】本题主要考查列代数式及整式的加减,熟练掌握列代数式及整式的加减是解题的关键.
4.将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a=9,宽为b=2,且a>b,AD=30,请求:
(1)长方形ABCD的面积;
(2)S1﹣S2的值.
【答案】(1)510;(2).
【分析】(1)先用含a和b的式子表示出CD的长,然后求得矩形ABCD的面积,从而代入求值;
(2)根据长方形的面积公式列式,然后代入求值.
【详解】(1)①由题意可得:CD=a+4b,
∴S长方形ABCD=AD•CD=AD(a+4b),
当a=9,b=2,AD=30时,
S长方形ABCD=30×(9+4×2)=30×17=510,
故长方形ABCD的面积为:510;
②由题意可得:S2=a(AD−3b),S1=4b(AD−a),
当a=9,b=2,AD=30时,
=
=
=
=.
【点睛】此题考查了整式的加减运算以及代数式求值问题,熟练掌握运算法则是解本题的关键.整式加减的应用时:(1)认真审题,弄清已知和未知的关系;(2)根据题意列出算式.
5.已知:b是最小的正整数,且a、b、c满足(c﹣5)2+|a+b|=0,请回答问题:
(1)请直接写出a、b、c的值.a=_____ ,b= ______ ,c= ______
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|﹣|x﹣1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值
【答案】(1) -1;1;5;(2) 4x+10或2x+12;(3)不变, BC-AB=2
【分析】(1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数的和是0,则每个数都是0,即可求得a,b,c的值;
(2)根据x的范围,确定x+1,x-1,x+5的符号,然后根据绝对值的意义即可化简;
(3)先求出BC=3t+4,AB=3t+2,从而得出BC-AB=2.
【详解】(1)∵b是最小的正整数,∴b=1.
根据题意得:c-5=0且a+b=0,
∴a=-1,b=1,c=5.
故答案是:-1;1;5;
(2)当0≤x≤1时,x+1>0,x-1≤0,x+5>0,
则:|x+1|-|x-1|+2|x+5|
=x+1-(1-x)+2(x+5)
=x+1-1+x+2x+10
=4x+10;
当1<x≤2时,x+1>0,x-1>0,x+5>0.
∴|x+1|-|x-1|+2|x+5|
=x+1-(x-1)+2(x+5)
=x+1-x+1+2x+10
=2x+12.
(3)不变.理由如下:
t秒时,点A对应的数为-1-t,点B对应的数为2t+1,点C对应的数为5t+5.
∴BC=(5t+5)-(2t+1)=3t+4,AB=(2t+1)-(-1-t)=3t+2,
∴BC-AB=(3t+4)-(3t+2)=2,
即BC-AB的值不随着时间t的变化而改变,BC-AB=2.
【点睛】本题考查了数轴与绝对值,整式的加减,通过数轴把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.
6.小明的爸爸以每件m元的成本价购进了30件甲种商品,以每件n元的成本价购进了40件乙种商品,且.
(1)在销售前小明的爸爸经市场调查发现,甲种商品比较畅销供不应求,乙种商品基本没人问津.为了尽快减少库存,但又不能亏本,小明的爸爸决定将甲种商品按成本价提高40%后标价出售;乙种商品按成本价的七折出售,则甲种商品的每件售价可表示为______(用含m的代数式表示),乙种商品的每件售价可表示为______(用含n的代数式表示);
(2)在(1)的条件下,将甲、乙商品全部售出,用含m、n的代数式表示小明爸爸的获利;
(3)若小明的爸爸将两种商品都以的平均价格一次打包全部出售,请判断他这次买卖是赚钱还是亏本,请说明理由.
【答案】(1),;(2);(3)赚钱,理由见解析
【分析】(1)根据甲种商品按成本价提高40%后标价出售;乙种商品按成本价的七折出售解答即可;
(2)根据总销售额减去总成本即可得出总获利;
(3)利用已知表示出总销售额减去总成本,判断正负即可得出结论.
【详解】解:(1)由题意得:甲种商品的每件售价为:,
乙种商品的每件售价为:,
故答案为:,;
(2)由题意得:,
故总获利为:;
(3)根据题意,这次买卖的利润为:,
∵,
∴,
∴,
∴这次买卖是赚钱.
【点睛】本题考查了列代数式以及整式的加减运算,正确表示出获利是解题的关键.
7.某超市在双十一期间对购物实行优惠,规定如下:
一次性购物货款
优惠办法
不超过200元
不予优惠
超过200元但不超过500元
九折优惠
超过500元
其中500元部分给予九折优惠,超过500元部分给予八折优惠
(1)王阿姨一次性购物700元,她实际付款 元.
(2)若顾客在该超市一次性购物货款为x元,用含x的代数式表示下列结果.
①当x超过200元但不超过500元时,实际付款 元;
②当x大于500元时,实际付款 元.
(3)如果王阿姨两次购物货款合计840元,第一次购物的货款为元(200<<300),用含的代数式表示:王阿姨两次购物实际付款一共多少元?
【答案】(1)610;(2)①0.9x;②0.8x+50;(3)0.1a+722
【分析】(1)让500元部分按9折付款,剩下的200元按8折付款即可;
(2)①当x超过200元但不超过500元时,实际付款=购物款×9折;
②当x大于500元时,实际付款=500×9折+超过500的购物款×8折;
(3)两次购物王阿姨实际付款=第一次购物款×9折+500×9折+(总购物款-第一次购物款-第二次购物款500)×8折,把相关数值代入即可求解.
【详解】解:(1)根据题意得,王阿姨一次性购物700元,实际付款:
500×0.9+(700-500)×0.8=610(元).
故答案为:610;
(2)若顾客在该超市一次性购物x元,
①当x超过200元但不超过500元时,实际付款0.9x元;
②当x大于500元时,实际付款500×0.9+0.8(x-500)=(0.8x+50)元.
故答案为:0.9x,(0.8x+50);
(3)根据题意可得:
两次购物王阿姨实际共付款:
0.9a+0.8(840-a-500)+500×0.9
=0.9a+0.8(340-a)+450
=0.1a+722.
答:两次购物王阿姨实际付款(0.1a+722)元.
【点睛】本题考查了列代数式以及整式加减的应用,解决本题的关键是得到不同购物款所得的实际付款的等量关系,难点是求第二问的第二次购物款应分9折和8折两部分分别计算实际付款.
8.如图,用三种大小不同的六个正方形和一个缺角的长方形拼成大长方形ABCD,其中 GH =1,HM =3,设BF=a
(1)用含a的代数式表示CN= cm,DN= cm
(2)用含a的代数式表示大长方形ABCD的周长
【答案】(1)(a+1),3a;(2)18a+8
【分析】(1)根据正方形的性质和线段的和差关系即可得出CN和DN,
(2)先求出长方形ABCD的长和宽,再用2×(长+宽)即可得出长方形ABCD的周长.
【详解】(1)CN=BF+HG=a+1,
DN=MN=NH-MH
=3NC-MH
=3×(a+1)-3
=3a;
(2)DC=CN+DN=a+1+3a=4a+1
BC=a×2+(a+1)×3=2a+3a+3=5a+3
C长ABCD=(4a+1+5a+3)×2
=18a+8.
【点睛】此题考查了列代数式和整式的加减,主要是能够用不同的方法表示同一个长方形的宽,注意各个正方形的边长之间的数量关系.
9.如图,用三种大小不同的5个正方形和1个长方形(阴影部分)拼成长方形ABCD,其中EF=3,最小的正方形的边长为x.
(1)FG= ,DG= ;(用含x的代数式表示)
(2)用含x的代数式表示长方形ABCD的周长,并求当x=6时长方形ABCD的周长.
【答案】(1)x+3,3x﹣3;(2)16x+6,102
【分析】(1)根据正方形的性质及线段的和差关系即可表示出FG和DG;
(2)先表示出长方形ABCD的长和宽,再表示出长方形的周长,把x=6代入即可求出答案.
【详解】解:(1)根据图形可知:
FG=x+3,
DG=HF=3x﹣EF=3x﹣3,
故答案为:x+3,3x﹣3;
(2)∵长方形的宽为:x+3+3x﹣3=4x,长方形的长为:3x+x+3=4x+3,
∴长方形ABCD的周长为:[4x+(4x+3)]×2=16x+6,
当x=6时,16x+6=16×6+6=102.
【点睛】本题考查了列代数式及代数式求值,理解各个正方形的边长之间的数量关系是解决问题的关键.
10.定义:若,则称与是关于的平衡数.
例如:若,则称与是关于3的平衡数.
(1)①2 与 是关于3的平衡数;
② 与 是关于3 的平衡数. (用含的代数式表示).
(2)若,判断与是否是关于0 的平衡数,并说明理由.
【答案】(1)①1,②;(2)a与b不是关于0的平衡数,理由见解析
【分析】(1)①根据平衡数的定义列式计算即可;
②根据平衡数的定义列式计算即可;
(2)首先去括号,合并同类项化简a,b,然后计算a+b的值即可进行判断.
【详解】解:(1)①∵3-2=1,
∴2与1是关于3的平衡数;
②∵3-(4-x)=3-4+x=x-1,
∴4-x与x-1是关于3的平衡数;
(2)
,
∵
∴a与b不是关于0的平衡数.
【点睛】本题考查了整式加减的实际应用,正确理解平衡数的定义是解题关键.
11.某超市在春节期间对顾客实行优惠,规定如下:
一次性购物
优惠办法
少于200元
不予优惠
低于500元但不低于200元
九折优惠
500元或超过500元
其中500元部分给予九折优惠,超过500元部分给予八折优惠
(1)王老师一次性购物650元,他实际付款 元.
(2)若顾客在该超市一次性购物元,当小于500元但不小于200元时,他实际付款 元,当大于或等于500元时,他实际付款 元.(用含的代数式表示)
(3)如果王老师两次购物货款合计810元,第一次购物的货款为元,用含的代数式表示:两次购物王老师实际共付款多少元?(要求列式并化简)
【答案】(1)570;(2),;(3)或元
【分析】(1)500元的部分按9折付款,剩下的150元按原价付款即可;
(2)当x小于500元但不小于200元时,实际付款=购物款×9折,当x大于或等于500元时,实际付款=500×9折+超过500的购物款×8折;
(3)分两种情况:a<200和200≤a<300分别计算,即可得出结果.
【详解】解:(1)根据题意得:
(元,
故答案为:570;
(2)若顾客在该超市一次性购物元,
当小于500元但不小于200元时,实际付款:元,
当大于或等于500元时,实际付款:,
故答案为:,;
(3)当时,两次购物王老师实际共付款:元,
当时,两次购物王老师实际共付款:元,
两次购物王老师实际共付款或元.
【点睛】本题考查了列代数式及求值,根据不同情况正确列出代数式是解决问题的关键.
12.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、b满足.
(1)______,______,______;(直接写得数)
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合(请写出过程);
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则______,______,______.(直接用含t的代数式表示)
(4)请问:的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1),1,7;(2)4,见解析;(3),,;(4)不变,12
【分析】(1)由非负数的性质可得,,从而求解的值,再由b是最小的正整数求解即可;
(2)先求解对折时折痕点对应的数,再计算与折痕点之间的距离即可得到答案;
(3)先表示运动后对应的数分别为: 再利用数轴上两点之间的距离公式进行计算可得答案;
(4)结合(3)问的结论计算,根据计算的结果进行作答即可.
【详解】解:(1)因为,
所以,,
所以,.
又因为b是最小的正整数,所以,,
答案:,,.
(2)由折痕点是线段AC的中点,
折痕点对应的数为:
对应的数为
点B与数4表示的点重合
故答案为:4.
(3)由题意可得:运动后对应的数分别为:
,
.
(4)解:不变.理由如下:
.
为定值,不会发生变化.
【点睛】本题考查的是数轴上两点之间的距离,绝对值非负性的应用,数轴上线段的中点对应的数的表示,列代数式,整式的加减运算的应用,掌握以上基础知识是解题的关键.
13.如图,正方形和正方形的边长分别为9和.
(1)写出表示阴影部分面积的代数式(结果要求化简);
(2)当时,求阴影部分的面积.
【答案】(1);(2)
【分析】(1)阴影部分面积两个正方形面积和减去两个直角三角形面积,把对应的三角形面积代入即可;
(2)直接把代入(1)中可求出阴影部分的面积.
【详解】解:(1),
;
(2)当时,
,
阴影部分的面积为.
【点睛】本题考查列代数式.准确把握图形间的关系,找到阴影部分的面积是哪些规则图形的面积差是解题的关键.
14.某商场销售一种西装和领带,西装每套定价1000元,领带每条定价200元.“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款 元.(用含x的代数式表示)若该客户按方案二购买,需付款 元.(用含x的代数式表示)
(2)若x=32,通过计算说明此时按哪种方案购买较为合算?
(3)当x=32时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
【答案】(1),;(2)方案一合算;(3)先按方案一购买20套西装并获赠20条领带,再按方案二购买12条领带,则需22160元.
【分析】(1)方案①付费为:套西装的价钱条领带的钱;方案②付费为:(套西装的钱+条领带的钱)×;
(2)将代入(1)中的代数式,分别计算即可;
(3)只买套西装按方案①付费,剩下的领带按折付费.
【详解】解:(1)方案①付费为:,
方案②付费为:,
故答案为:,;
(2)若x=32,则方案①付费为:元,
方案②付费为:元,
∵,
∴则方案①购买较合算;
(3)只买套西装按方案①付费,得到获赠的条领带,剩下的领带按折付费,
总费用为:元.
【点睛】本题考查了列代数式以及代数式求值,得到所给方案计算的等量关系是解决本题的关键.
15.某水果经销户从水果市场批发了苹果和桔子共100千克,苹果和桔子当天的批发价、零售价如下表:
品 名
苹 果
桔 子
批发价(元/ kg)
5.2
3.2
零售价(元/ kg)
8.8
6.2
(1)若经销户分别批发了60 kg苹果和40 kg桔子,那么当天卖完这些苹果和桔子该经销户能盈利 元.
(2)若经销户批发了m kg苹果,当天卖完这些苹果和桔子经销户能盈利多少元?(用含m的代数式表示,要求化简)
【答案】(1)336;(2)0.6m+300.
【分析】(1)根据题意可得利润为60×(8.8-5.2)+40×(6.2-3.2),进而计算即可求得答案;
(2)根据题意可得利润为m·(8.8-5.2)+(100-m)×(6.2-3.2),进而化简即可求得答案.
【详解】解:(1)根据题意可得:
60×(8.8-5.2)+40×(6.2-3.2)
=60×3.6+40×3
=216+120
=336(元),
故答案为:336 ;
(2)根据题意可得:
m·(8.8-5.2)+(100-m)×(6.2-3.2)
=3.6m+3(100-m)
=3.6m+300-3m
=0.6m+300.
【点睛】本题考查了有理数的混合运算以及整式加减的实际应用,熟练掌握整式加减的运算法则是解决本题的关键.
16.某电器商销售一种微波炉和电磁炉,微波炉每台定价900元,电磁炉每台定价300元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的80%付款.
现某客户要到该卖场购买微波炉2台,电磁炉x台(x>2).
(1)若该客户按方案一购买,需付款 元 (用含x的代数式表示) .
若该客户按方案二购买,需付款 元 (用含x的代数式表示) .
(2)若x=6时,通过计算说明此时按哪种方案购买较为合算?
(3)当x=6时,你能给出一种更为省钱的购买方案吗?试写出购买方案,并计算需要付款多少元?
【答案】(1)(300x+1200),(240x+1440);(2)按方案二购买较合算;(3)先按方案一购买2台微波炉送2台电磁炉,再按方案二购买4台电磁炉,共2760元.
【分析】(1)根据题目提供的两种不同的付款方式列出代数式即可;
(2)将x=6代入求得的代数式中即可得到费用,然后比较即可得到选择哪种方案更合算;
(3)根据题意考可以得到先按方案一购买2台微波炉再送2台电磁炉,再按方案二购买3台电磁炉更合算.
【详解】解:(1)方案一: ,
方案二: ;
故答案为:(300x+1200),(240x+1440);
(2)当x=6时,方案一:300×6+1200=3000(元),
方案二:240×6+1440=2880(元),
按方案二购买较合算;
(3)先按方案一购买2台微波炉送2台电磁炉,再按方案二购买4台电磁炉,
共2×900+300×4×80%=2760(元).
【点睛】本题考查了列代数式和求代数式的值的相关的题目,解题的关键是认真分析题目并正确的列出代数式.
17.某设计公司设计出如图所示的一个图案(图中阴影部分),其中长方形的长为,宽为y,扇形的半径为y.
(1)用含x、y的代数式表示图案(图中阴影部分)的面积S;
(2)当x=12,y=8时,求面积S的值.(结果保留π)
【答案】(1)xy+y2;(2)16π+16
【分析】(1)用矩形的面积加四分之一圆的面积减去大三角形的面积即可求出答案;
(2)将x=12,y=8代入求解即可.
【详解】(1)阴影部分的面积为
;
(2)当x=12,y=8时,
.
【点睛】本题主要考查整式加减的应用,掌握整式加减的运算法则是关键.
18.某超市在双十一期间对顾客实行优惠,规定如下:
一次性购物
优惠办法
少于200元
不予优惠
低于500元但不低于200元
八折优惠
500元或超过500元
其中500元部分给予八折优惠,超过500元部分给予七折优惠
(1)若王老师一次性购物600元,他实际付款______元.若王老师实际付款160元,那么王老师一次性购物可能是______元;
(2)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款_______元,当x大于或等于500元时.他实际付款_____元(用含x的代数式表示并化简);
(3)如果王老师有两天去超市购物原价合计850元,第一天购物的原价为a元(200<a<300),用含a的代数式表示:两天购物王老师实际一共付款多少元?当a=250元时.王老师两天一共节省了多少元?
【答案】(1)470元;200或160元;(2)0.8x;(0.7x+50);(3)共节省180元.
【分析】(1)根据表格中的数量关系,列出算式,即可;
(2)根据表格中的数量关系,列出代数式,即可;
(3)分别列出第一天购物和第二天购物的代数式,再求和,最后代入求值即可.
【详解】(1)解:王老师一次性购物600元,他实际付款:500×0.8+100×0.7=470(元),
王老师实际付款160元,那么王老师一次性购物可能是:160÷0.8=200元或160元
故答案是:470;200或160;
(2)顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款0.8x元;当x大于或等于500元时.他实际付款:(0.7x+50)元,
故答案是:0.8x;(0.7x+50);
(3)解:第一天购物实际付款:0.8a元,
第二天购物实际付款:500×0.8+0.7(850-a-500)=(645-0.7a)元,
两天共付款:(0.1a+645) 元,
当a=250元时,0.1a+645=670元;
所以共节省:850-670=180元.
【点睛】本题主要考查列代数式以及整式的加减运算,理解题目中的数量关系,列出代数式,是解题的关键.
相关资料
更多









