苏科版九年级下册7.6 用锐角三角函数解决问题测试题

这是一份苏科版九年级下册7.6 用锐角三角函数解决问题测试题，共18页。试卷主要包含了吉林省广播电视塔等内容，欢迎下载使用。

7.6用锐角三角函数解决问题同步练习

1．如图，海面上一艘船由西向东航行，在A处测得正东方向上一座灯塔的最高点C的仰角为31°，再向东继续航行30m到达B处，测得该灯塔的最高点C的仰角为45°，根据测得的数据，计算这座灯塔的高度CD（结果取整数）．（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

2．李老师为了准备网课直播，购买了一个三脚架，如图①所示，图②为其截面示意图．测得OC＝OD＝60cm，AO＝100cm，∠COB＝∠DOB＝32°．求点A到地面CD的高度（结果精确到1cm）．
（参考数据：sin32°＝0.53，cos32°＝0.85，tan32°＝0.62．）

3．如图1，是某人拿自拍杆用手机进行自拍的实物图，图2是由其抽象出来的几何图形，AC是可以伸缩的自拍杆，其端点A离地面BD的高度AH为1.4m，当自拍杆AC的长度为0.9m，张角∠HAC为118°时，求自拍杆的另一端点C离地面的高度（结果保留小数点后一位：参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）


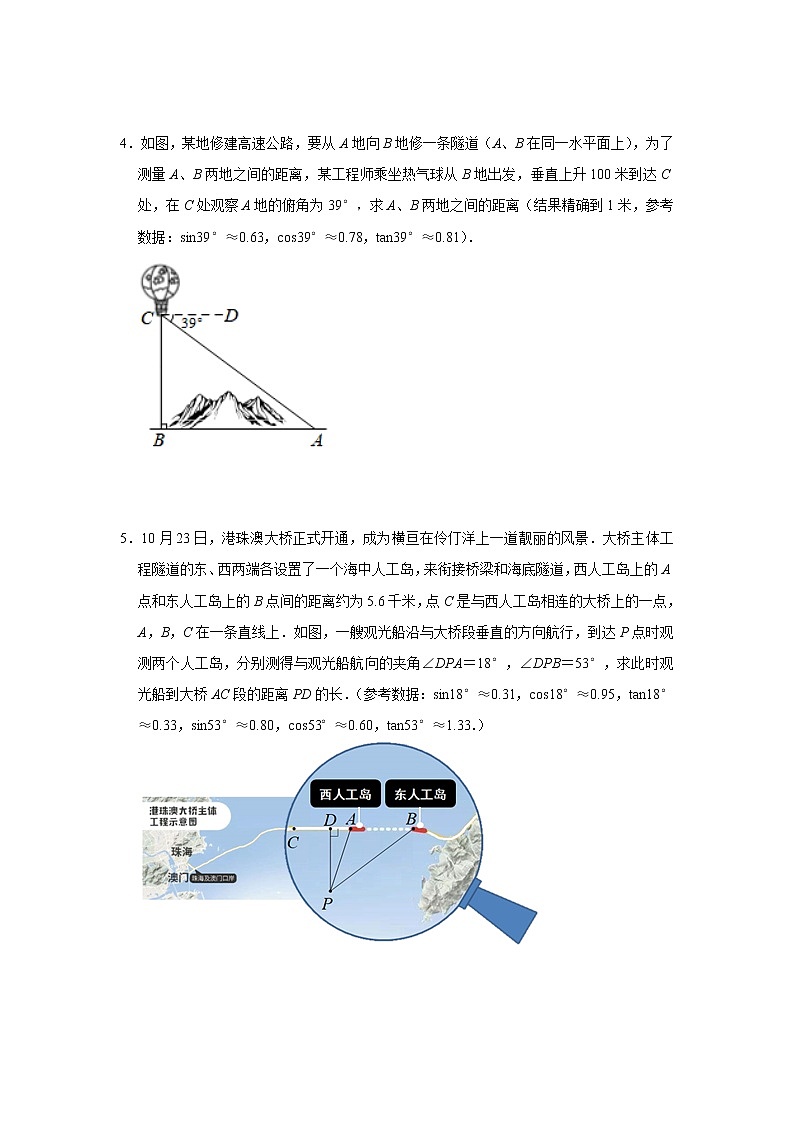
4．如图，某地修建高速公路，要从A地向B地修一条隧道（A、B在同一水平面上），为了测量A、B两地之间的距离，某工程师乘坐热气球从B地出发，垂直上升100米到达C处，在C处观察A地的俯角为39°，求A、B两地之间的距离（结果精确到1米，参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）．



5．10月23日，港珠澳大桥正式开通，成为横亘在伶仃洋上一道靓丽的风景．大桥主体工程隧道的东、西两端各设置了一个海中人工岛，来衔接桥梁和海底隧道，西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米，点C是与西人工岛相连的大桥上的一点，A，B，C在一条直线上．如图，一艘观光船沿与大桥段垂直的方向航行，到达P点时观测两个人工岛，分别测得与观光船航向的夹角∠DPA＝18°，∠DPB＝53°，求此时观光船到大桥AC段的距离PD的长．（参考数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.33，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33．）




6．被誉为“中原第一高楼”的郑州会展宾馆（俗称“大玉米”）坐落在风景如画的如意湖，是来郑州观光的游客留影的最佳景点．学完了三角函数知识后，刘明和王华同学决定用自己学到的知识测量“大玉米”的高度，他们制订了测量方案，并利用课余时间完成了实地测量．测量项目及结果如下表：
项目
内容
课题
测量郑州会展宾馆的高度
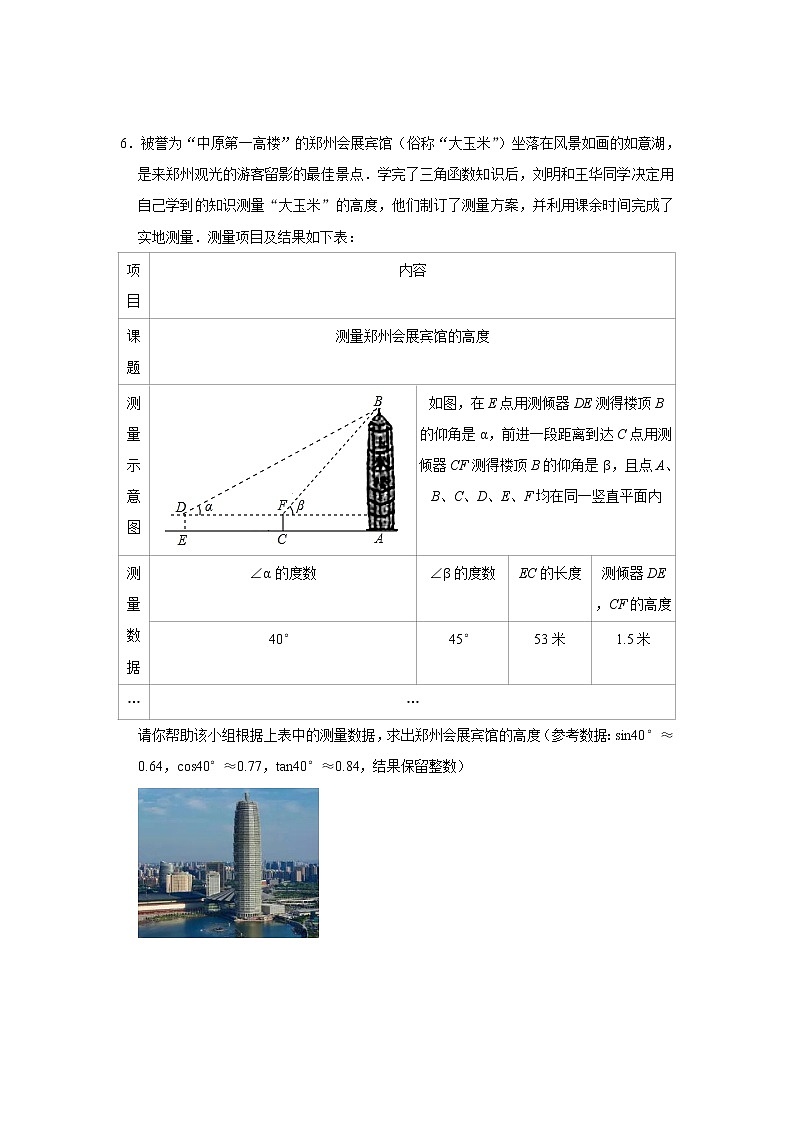
测量示意图

如图，在E点用测倾器DE测得楼顶B
的仰角是α，前进一段距离到达C点用测倾器CF测得楼顶B的仰角是β，且点A、B、C、D、E、F均在同一竖直平面内
测量数据
∠α的度数
∠β的度数
EC的长度
测倾器DE
，CF的高度
40°
45°
53米
1.5米
…
…
请你帮助该小组根据上表中的测量数据，求出郑州会展宾馆的高度（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果保留整数）




7．图①、图②分别是一把水平放置的椅子的效果图与椅子侧面的示意图，椅子高为AC，椅面宽BE为60cm，椅脚高ED为35cm，且AC⊥BE，AC⊥CD，AC∥ED，从点A测得点E的俯角为53°，求椅子的高AC（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）．

8．宋家州主题公园拟修建一座柳宗元塑像，如图所示，柳宗元塑像（塑像中高者）DE在高13.4m的假山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进10m到达B处，测得塑像顶部D的仰角为60°，求柳宗元塑像DE的高度．
（精确到1m．参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67，≈1.73）

9．吉林省广播电视塔（简称“吉塔”）是我省目前最高的人工建筑．某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度，如图，将无人机置于距离“吉塔”水平距离138米的点C处．从无人机上观测塔尖A的仰角为30°．观测塔基座中心点B的俯角为45°．求“吉塔”的高度（结果保留整数，参考数据：≈1.73）．


10．如图，这是某水库大坝截面示意图，张强在水库大坝顶CF上的瞭望台D处，测得水面上的小船A的俯角为40°，若DE＝3米，CE＝2米，CF平行于水面AB，瞭望台DE垂直于坝顶CF，迎水坡BC的坡度i＝4：3，坡长BC＝10米，求小船A距坡底B处的长．（结果保留0.1米）（参考数据：sin40°≈0.64，cos40°＝0.77，tan40°≈0.84）


11．如图，某校数学兴趣小组要测量吉林北山革命烈士纪念塔的高度，在与塔底部B相距20m的点D处，即BD＝20m，用高1.6m的测角仪CD测得该塔顶端A的仰角∠ACE＝53°．求纪念塔AB的高度．（结果精确到1m）（参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）


12．为了测量某单位院内旗杆AB的高度，在地面距离旗杆底部B的15米C处放置高度为1.8米的测角仪CD，测得旗杆顶端A的仰角（∠ADE）为54°．求旗杆AB的高度（结果精确到1米）．（参考数据：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38）


13．某市为了加快5G网络信号覆盖，在市区附近小山顶架设信号发射塔，如图，山顶上有一个信号塔AC，已知信号塔高AC＝21米，在山脚下点B处测得塔底C的仰角∠CBD＝36.9°，塔顶A的仰角∠ABD＝42.0°．求山高CD（点A，C，D在同一条竖直线上）．（参考数据：tan36.9°≈0.75．sin36.9°≈0.60．tan42.0°≈0.90．）

14．近年来，成都IFS商业大楼成了网红打卡地，楼上“翻墙”的大熊猫给游客留下了深刻的印象．小明使用测角仪测量熊猫C处距离地面AD的高度，他在甲楼底端A处测得熊猫C处的仰角为53°，在甲楼B处测得熊猫C处的仰角为45°，已知AB＝4.5米，求熊猫C处距离地面AD的高度．（结果保留一位小数，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

15．如图，某旅游景区为方便游客，修建了一条东西走向的木栈道AB，在景区道路CD的C处测得栈道一端A位于北偏西42°方向，另一端B位于北偏东45°方向，又测得AC为100米，求木栈道AB的长度（结果保留整数）．
（参考数据：sin42°≈，cos42°≈，tan42°≈）

16．已知，如图，在坡顶A处的同一水平面上有一座古塔BC，数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°，然后他们沿着坡度为1：2.4的斜坡AP攀行了26米，在坡顶A处又测得该塔的塔顶B的仰角为76°．求：
（1）坡顶A到地面PO的距离；
（2）古塔BC的高度（结果精确到1米）．
（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）


17．数学爱好小组要测量5G信号基站高度，一名同学站在距离5G信号基站30m的点E处，测得基站顶部的仰角∠ACD＝52°，已知测角仪的高度CE＝1.5m．求这个5G信号基站的高AB（精确到1m）．（参考数据：sin52°＝0.79，cos52°＝0.62，tan52°＝1.28）


18．如图，为测量小岛A到公路BD的距离，先在点B处测得∠ABD＝37°，再沿BD方向前进150m到达点C，测得∠ACD＝45°，求小岛A到公路BD的距离．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）



19．如图，甲、乙两栋大楼相距78米，一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°．如果甲楼的高为34米，求乙楼的高度是多少米？（结果精确到0.1米）
【参考数据：sin27°＝0.45，cos27°＝0.89，tan27°＝0.51】

20．如图，有一电线杆AB直立于地面，它的影子正好射在地面BC段和与地面成45°角的土坡CD上，已知∠BAD＝60°，BC＝8米，CD＝2米，求电线杆AB的高．（结果保留3个有效数字，≈1.732）


参考答案
1．解：在Rt△CAD中，，
则，
在Rt△CBD中，∠CBD＝45°，
∴BD＝CD，
∵AD＝AB+BD，
∴，
解得，CD＝45（m）．
答：这座灯塔的高度CD约为45m．
2．解：如图所示：延长OB交DC于点E，
∵OC＝OD＝60cm，∠COB＝∠DOB＝32°，
∴AO⊥CD，
∴cos32°＝＝，
解得：OE≈60×0.85＝51（cm），
则AO+EO≈100+51＝151（cm）．
答：点A到地面CD的高度约为151cm．

3．解：作CE⊥BD于E，AF⊥CE于F，
∴四边形AHEF为矩形，
∴EF＝AH＝1.4m，∠HAF＝90°，
∴∠CAF＝∠CAH﹣∠HAF＝118°﹣90°＝28°，
在Rt△ACF中，sin∠CAF＝，
∴CF＝0.9sin28°＝0.9×0.47≈0.423m，
CE＝CF+EF＝0.423+1.4≈1.8m，
答：点C离地面的高度为1.8m；

4．解：在Rt△ABC中，∵∠ABC＝90°，∠A＝39°，
∴tan39°＝，
∴AB＝≈123（米）．
答：A、B两地之间的距离约为123米．
5．解：在Rt△DPA中，
∵tan∠DPA＝，
∴AD＝PD•tan∠DPA，
在Rt△DPB中，
∵tan∠DPB＝，
∴BD＝PD•tan∠DPB，
∴AB＝BD﹣AD＝PD•（tan∠DPB﹣tan∠DPA），
∵AB＝5.6，∠DPB＝53°，∠DPA＝18°，即5.6＝（tan53°﹣tan18°）•PD，
∴PD＝＝5.6，
则此时观光船到大桥AC段的距离PD的长为5.6千米．
6．解：由题意可得：设BN＝FN＝x，
则tan40°＝＝≈0.84，
解得：x＝278.25，
故AB＝278.25+1.5≈280（m），
答：郑州会展宾馆的高度为280m．

7．解：∵AC⊥BE，AC⊥CD，AC∥ED，
∴四边形BCDE是矩形，∠AEB＝53°，
∴BC＝DE＝35（cm），
在Rt△ABE中，∠ABE＝90°，tan∠AEB＝，BE＝60cm，
∴AB＝BE•tan∠AEB＝60×tan53°≈60×1.3＝78，
∴AC＝AB+BC＝78+35＝113（cm），
即椅子的高约为113cm．
8．解：∵∠ACE＝90°，∠CAE＝34°，CE＝13.4m，
∴，
∴，
∵AB＝10m，
∴BC＝AC﹣AB＝20﹣10＝10m，
在Rt△BCD中，，
∴，
∴DE＝CD﹣EC＝17.3﹣13.4＝3.9≈4m．
答：柳宗元塑像DE的高度约为4m．
9．解：如图，根据题意，有∠ACH＝30°，∠HCB＝45°，CH＝138米，

在Rt△ACH中，∵tan∠ACH＝，
∴tan30°＝，
∴AH＝138×＝46≈79.58（米），
在Rt△BCD中，∵∠DCB＝45°，CD＝138米，
∴BH＝CH＝138米，
∴AB＝AH+BH≈79.58+138≈218（米）．
答：“吉塔”的高度约为218米．
10．解：如图，延长DE交AB延长线于点P，作CQ⊥AP于点Q，
∵CE∥AP，
∴DP⊥AP，
∴四边形CEPQ为矩形，
∴CE＝PQ＝2（米），CQ＝PE，
∵i＝，
∴设CQ＝4x、BQ＝3x，
由BQ2+CQ2＝BC2可得（4x）2+（3x）2＝102，
解得：x＝2或x＝﹣2（舍），
则CQ＝PE＝8（米），BQ＝6（米），
∴DP＝DE+PE＝11（米），
在Rt△ADP中，∵AP＝≈13.1（米），
∴AB＝AP﹣BQ﹣PQ＝13.1﹣6﹣2＝5.1（米）．

11．解：由题意知，EC＝BD＝20m，EB＝CD＝1.6m，∠AEC＝90°，
∵tan∠ACE＝，
∴AE＝EC×tan∠ACE≈20×1.33＝26.6（m），
∴AB＝AE+EB≈26.6+1.6≈28（m），
答：纪念塔AB的高度约为28m．
12．解：在Rt△ADE中，
∵∠ADE＝54°，
∴AE＝DE•tan∠ADE≈15×1.38≈20.7（米），
∵BE＝CD＝1.8（米），
∴AB＝AE+BE＝20.7+1.8＝22.5≈23（米）．
答：旗杆AB的高度约为23米．
13．解：由题意得，在Rt△ABD和Rt△CBD中，
AD＝BD•tan∠ABD≈0.9BD，CD＝BD•tan∠CBD≈0.75BD，
∴AC＝AD﹣CD＝0.15BD，
∵AC＝21米，
∴BD＝140米，
∴CD＝0.75BD＝105（米），
答：山高CD为105米．
14．解：如图，过点B作BE⊥CD于点E，

由题意可知：
∵∠CBE＝45°，∠CAD＝53°，AB＝4.5米，
∵∠ABE＝∠BED＝∠ADE＝90°，
∴四边形ABED是矩形，
∴BE＝AD，DE＝AB＝4.5米，
设CE＝x，则CD＝CE+DE＝x+4.5，
在Rt△CEB中，BE＝＝＝x，
在Rt△ADC中，CD＝AD•tan53°，
即x+4.5＝x•tan53°，
∴x≈13.64，
∴CE＝13.64（米），
∴CD＝CE+DE＝13.64+4.5＝18.14≈18.1（米）．
答：熊猫C处距离地面AD的高度为18.1米．
15．解：过C作CE⊥AB于E，如图所示：
则∠CEA＝∠CEB＝90°，
由题意得：∠ACE＝42°，∠BCE＝45°，
∴△BCE是等腰直角三角形，
∴BE＝CE，
∵sin∠ACE＝，cos∠ACE＝，
∴AE＝AC×sin42°≈100×＝67.5（米），
CE＝AC×cos42°≈100×＝75（米），
∴BE＝CE＝75米，
∴AB＝AE+BE＝67.5+75＝142.5≈143（米）；
答：木栈道AB的长度为143米．

16．解：（1）过点A作AH⊥PO，垂足为点H，
∵斜坡AP的坡度为1：2.4，
∴＝，
设AH＝5k，则PH＝12k，由勾股定理，得AP＝13k，
∴13k＝26，
解得k＝2，
∴AH＝10，
答：坡顶A到地面PO的距离为10米．

（2）延长BC交PO于点D，
∵BC⊥AC，AC∥PO，
∴BD⊥PO，
∴四边形AHDC是矩形，CD＝AH＝10，AC＝DH，
∵∠BPD＝45°，
∴PD＝BD，
设BC＝x，则x+10＝24+DH，
∴AC＝DH＝x﹣14，
在Rt△ABC中，tan76°＝，即≈4.01．
解得x≈19．
答：古塔BC的高度约为19米．

17．解：如图，过点C作CD⊥AB，垂足为D．则四边形CEBD是矩形，BD＝CE＝1.5m，
在Rt△ACD中，CD＝EB＝30m，∠ACD＝52°
∵tan∠ACE＝，
∴AD＝CD•tan∠ACD≈30×1.28＝38.4（m）．
∴AB＝AD+BD＝38.4+1.5≈40（m）．
答：这个5G信号基站的高AB约为40m．

18．解：过A作AE⊥CD垂足为E，设AE＝x米，
在Rt△ABE中，tanB＝，
∴BE＝＝x，
在Rt△ABE中，tan∠ACD＝，
∴CE＝＝x，
∵BC＝BE﹣CE，
∴x﹣x＝150，
解得：x＝450．
答：小岛A到公路BD的距离为450米．

19．解：如图，在△ABE中，有BE＝tan27°×AE＝0.51×78＝39.78（米），
故BD＝ED+BE＝34+39.78≈73.8（米）．
答：乙楼的高度约为73.8米．

20．解：延长AD交BE的延长线于点F，则∠F＝30°，
∵∠DCE＝45°，DE⊥CF，CD＝2 米，
∴CE＝DE＝2，
在直角三角形DEF中，EF＝＝2 米，
∴BF＝BC+CE+EF＝（10+2 ）米，
在直角三角形ABF中，AB＝BF×tan30°＝+2≈7.77米．