初中数学人教版九年级下册27.2.1 相似三角形的判定精品课件ppt

这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定精品课件ppt，共17页。PPT课件主要包含了知识回顾，新课导入，问题导入，知识讲解，相似三角形判定等内容，欢迎下载使用。
判断两个三角形相似,你有哪些方法？
三个角分别相等，三条边成比例的两个三角形叫做相似三角形. （不常用）
平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
方法3：三边成比例的两个三角形相似.
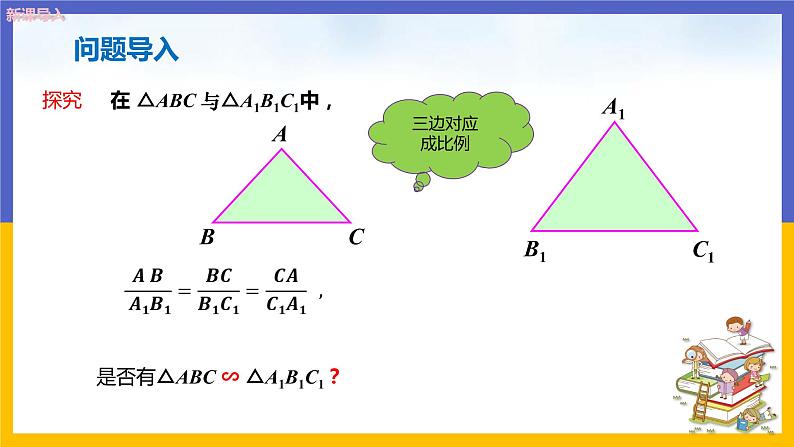
是否有△ABC ∽ △A1B1C1？
在 △ABC 与△A1B1C1中，
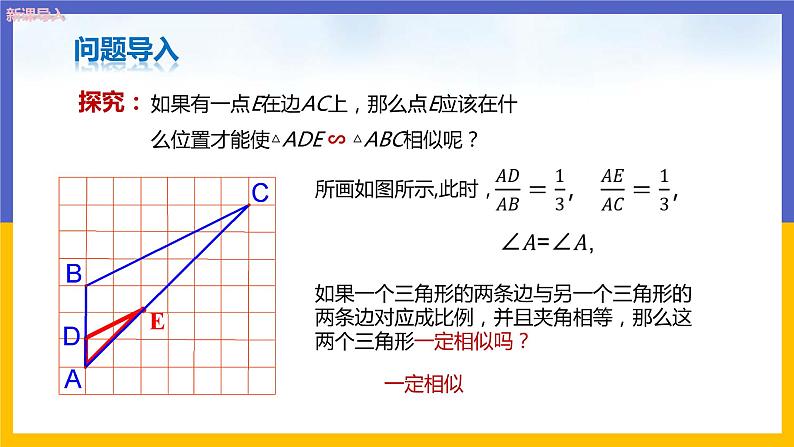
如果有一点E在边AC上，那么点E应该在什么位置才能使△ADE ∽ △ABC相似呢？
如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形一定相似吗？
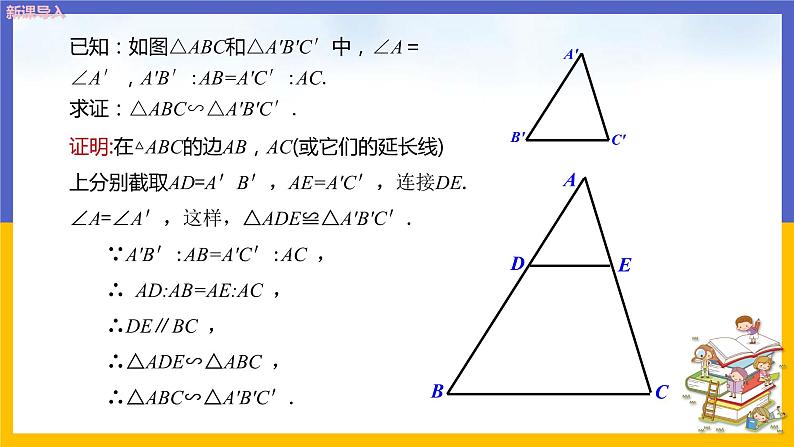
已知：如图△ABC和△A′B′C′中，∠A＝∠A′，A′B′:AB=A′C′:AC.求证：△ABC∽△A′B′C′.
证明:在△ABC的边AB，AC(或它们的延长线)上分别截取AD=A′B′，AE=A′C′，连接DE.∠A=∠A′，这样，△ADE≌△A′B′C′.
∵A′B′:AB=A′C′:AC ， ∴ AD:AB=AE:AC ，∴DE∥BC ，∴△ADE∽△ABC ，∴△ABC∽△A′B′C′.
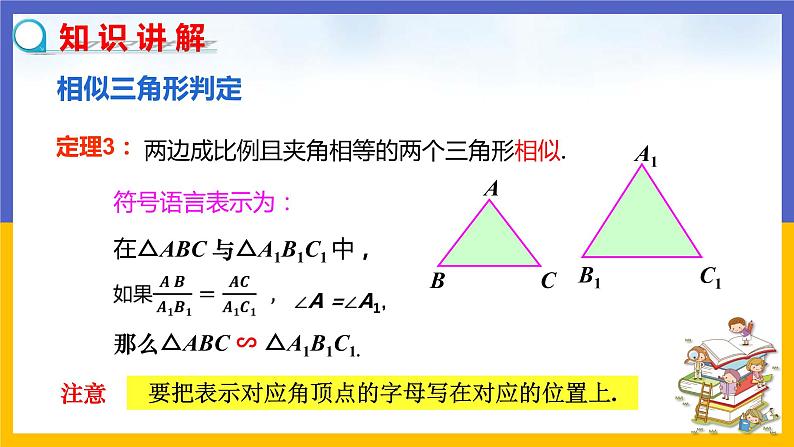
　　两边成比例且夹角相等的两个三角形相似.
那么△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
在△ABC 与△A1B1C1 中，
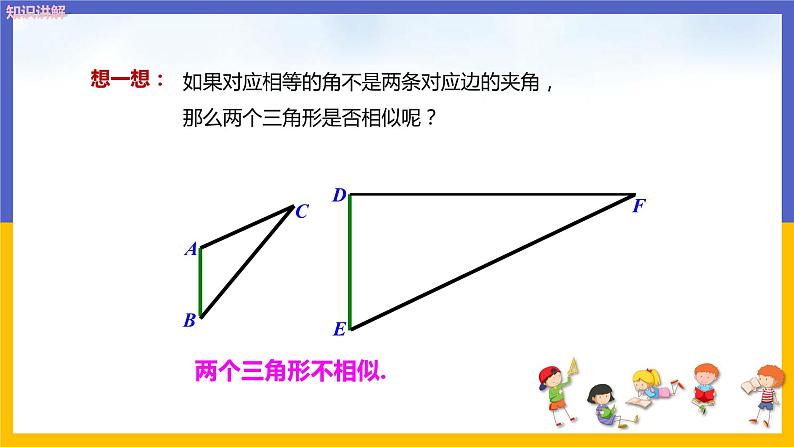
如果对应相等的角不是两条对应边的夹角，那么两个三角形是否相似呢？
证明：设正方形的边长为a. ∵ 四边形ABCD为正方形，∴ AD＝BC＝CD＝a.
如图所示，在正方形ABCD 中，P 是BC 上的一点，且BP ＝ 3PC，Q 是CD 的中点. 求证： △ ADQ ∽ △ QCP.
又∵∠ D ＝∠ C ＝ 90°，
∴ △ ADQ ∽ △ QCP.
1.如图，在△ABC中，点D在线段BC上，且△ABC∽△DBA，则下列结论一定正确的是（ ）A.AB2=BC·BD B.AB2=AC·BD C.AB·AD=BD·BC D.AB·AD=AD·CD
2.如图，在△ABC中，∠C=90°，D是AC上一点，DE⊥AB于点E，若AC=8，BC=6，DE=3，则AD的长为（　）A．3 B．4 C．5 D．6
1.如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．若OA：OC=0B：OD，则下列结论中一定正确的是 ( ) .A．①与②相似 B．①与③相似 C．①与④相似 D．②与④相似
解析：根据两边对应成比例且夹角相等得选择项.
2.已知：如图，在△ABC中，P是AB边上的一点，连接CP．试增添一个条件使△ ACP∽△ABC．
⑴∵∠A=∠A，∴当∠1= ∠ACB (或∠2= ∠B)时,△ACP∽△ABC .⑵ ∵∠A=∠A，∴当AC:AP＝AB:AC时， △ ACP∽△ABC.
所以，增添的条件可以是∠1= ∠ACB 或∠2= ∠B 或AC:AP＝AB:AC.
不同意，理由如下： ∵AC＝AE+CE，而AC＝6，CE＝2.1， ∴ AE＝6-2.1＝3.9 ，∴ AE：AB =3.9：7.8=1：2，AD：AC =3：6=1：2，∴ AE：AB =AD：AC，又 ∵∠A=∠A， ∴ △ADE∽△ACB．
本节课学习了哪些主要内容？
定理1：平行于三角形一边的直线和其他两边,所构成的三角形与原三角形相似;定理2：三边成比例的两个三角形相似;定理3：两边成比例且夹角相等的两个三角形相似.
两边对应成比例且夹角相等的两个三角形相似.
学过的相似三角形的判定：
教科书第34页练习第1题，第2（2）题．