人教版九年级下册26.1.2 反比例函数的图象和性质课前预习课件ppt

这是一份人教版九年级下册26.1.2 反比例函数的图象和性质课前预习课件ppt，共33页。PPT课件主要包含了学习目标，课时讲解，课时流程，知识点，反比例函数的图象，感悟新知，解列表，反比例函数的性质，k＜2等内容，欢迎下载使用。
反比例函数的图象反比例函数的性质反比例函数 (k ≠ 0)中k 的几何性质
1. 图象的画法(描点法)：(1)列表：先取一些自变量的值，在原点的两边取三对或三对以上互为相反数的值．(2)描点：根据表中提供的数据，即点的坐标，在平面直角坐标系中描出对应的点．(3)连线：用平滑的曲线顺次把这些点连接起来并延伸.
2. 图象的特点：(1)反比例函数 (k 为常数，k ≠ 0)的图象是双曲线.(2)反比例函数图象的两支分别位于第一、第三象限或第二、第四象限．(3)双曲线的两支都无限接近坐标轴，但永远不与坐标轴相交．
(4)双曲线既是中心对称图形(对称中心是原点)，又是轴对称图形(对称轴是直线y=x 和直线y=－x). 如图26.1-2.
特别提醒●由于反比例函数图象的两个分支关于原点对称，所以只要画出它在一个象限内的分支，就可以对称地画出另一个分支.●画实际问题中的反比例函数的图象时，要考虑自变量取值范围的限制，一般地，实际问题的图象是反比例函数图象在第一象限内的一支或其中一部分.
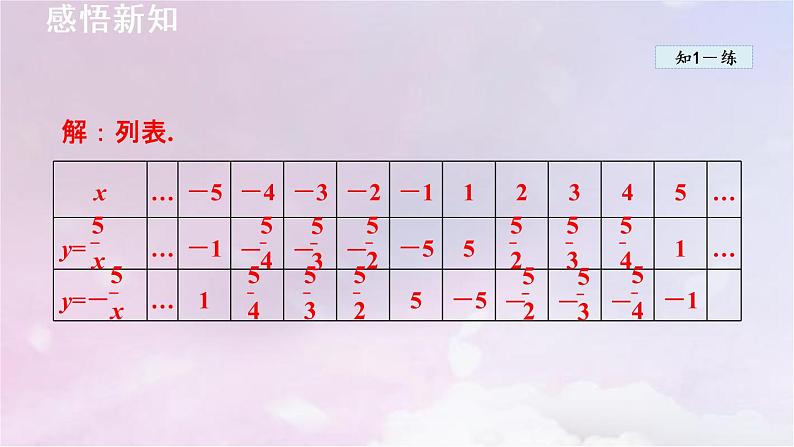
在同一平面直角坐标系中画出反比例函数y= 和y=－ 的图象.
解题秘方：紧扣画图象的步骤“一列、二描、三连”作图.
描点、连线得到如图26.1-3 所示的图象.
1-1. 已知函数y=(m－2)·xm2－5 是反比例函数.(1)求m 的值.
(2)根据函数解析式完成下表.
(3)以表中各组对应值为点的坐标，在如图所示的平面直角坐标系中描点并画出函数图象.
解：函数图象如图所示．
反比例函数的性质主要研究它的图象的位置和函数值的增减情况，如下表所示.
特别提醒在描述反比例函数的增减性时，必须指明“在每一个象限内”.因为当k ＞ 0(k ＜ 0) 时，整个函数不是y随x的增大而减小( 增大)，而是函数在每一个象限内，y随x的增大而减小(增大)，所以笼统地说“对于函数y= ，y 随x的增大而减小”是错误的.
已知反比例函数y= (m≠0)的图象过点(－3，－12)，且反比例函数y= 的图象位于第二、第四象限.(1)求m 的值；(2)对于y= ，当x ﹥ 2 时，求y 的取值范围.
解题秘方：紧扣“k 的符号、双曲线的位置、函数的增减性三者相互依存，知一推二”这一规律解题.
解：(1)把点(－3，－12)的坐标代入y= 中，得－12= ，∴ m2=36，∴ m=±6.∵反比例函数y= 的图象位于第二、第四象限，∴ m2，∴此部分图象在第四象限.当x=2 时，y=－ =－3. ∵在第四象限内，y 随x 的增大而增大，∴当x>2 时，－3