人教版数学八年级下册18.1.3目标三从一组对边的角度判定平行四边形课件

这是一份人教版数学八年级下册18.1.3目标三从一组对边的角度判定平行四边形课件，共13页。

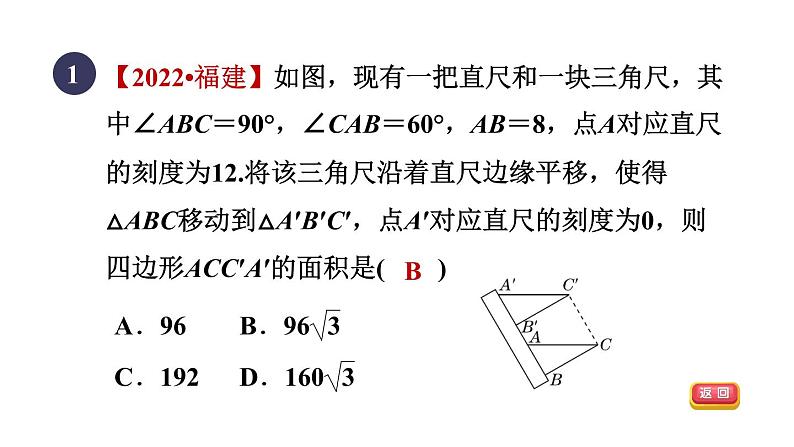
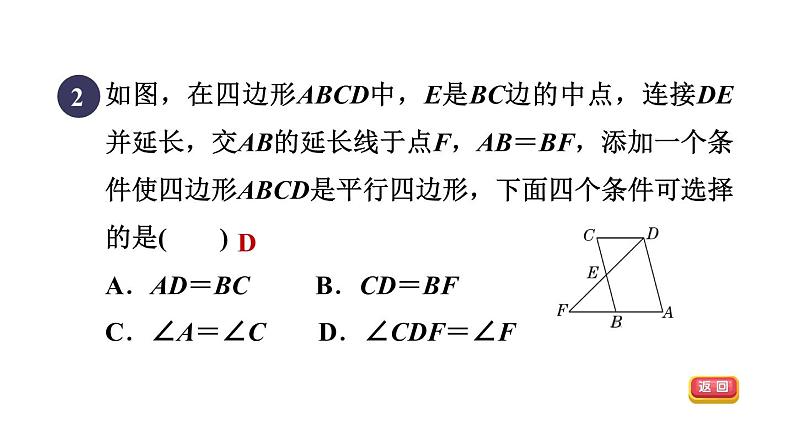
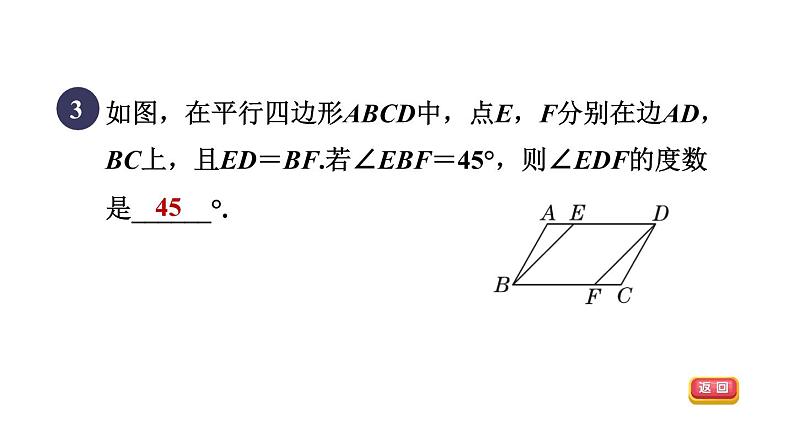
人教版 八年级下第十八章 平行四边形目标三　从一组对边的角度判定平行四边形平行四边形的判定18.1.3 B45D答 案 呈 现习题链接【2022•福建】如图，现有一把直尺和一块三角尺，其中∠ABC＝90°，∠CAB＝60°，AB＝8，点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移，使得△ABC移动到△A′B′C′，点A′对应直尺的刻度为0，则四边形ACC′A′的面积是(　　)1BD2如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于点F，AB＝BF，添加一个条件使四边形ABCD是平行四边形，下面四个条件可选择的是(　　)A．AD＝BC 　 B．CD＝BFC．∠A＝∠C 　 D．∠CDF＝∠F345如图，在平行四边形ABCD中，点E，F分别在边AD，BC上，且ED＝BF.若∠EBF＝45°，则∠EDF的度数是______°.4【2022•河池】如图，点A，F，C，D在同一直线上，AB＝DE，AF＝CD，BC＝EF.(1)求证：∠ACB＝∠DFE；解：如图，四边形BFEC是平行四边形．理由如下：由(1)可知，∠ACB＝∠DFE，∴BC∥EF.又∵BC＝EF，∴四边形BFEC是平行四边形．(2)连接BF，CE，直接判断四边形BFEC的形状．5【2022•内江】如图，在▱ABCD中，点E，F在对角线BD上，且BE＝DF.求证：(1)△ABE≌△CDF；解：由(1)可知△ABE≌△CDF，∴AE＝CF，∠AEB＝∠CFD.∴180°－∠AEB＝180°－∠CFD，即∠AEF＝∠CFE.∴AE∥CF.∴四边形AECF是平行四边形．(2)四边形AECF是平行四边形．6已知：如图，在平行四边形ABCD中，延长DA到点E，延长BC到点F，使得AE＝CF，连接EF，分别交AB，CD于点M，N，连接DM，BN.求证：(1)△AEM≌△CFN；解：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.由(1)得AM＝CN，∴BM＝DN.又∵BM∥DN，∴四边形BMDN是平行四边形．(2)四边形BMDN是平行四边形．